Однородные дифференциальные уравнения первого порядка
Функция 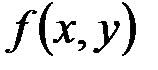 называется однородной функцией
называется однородной функцией 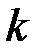 – того измерения, если при любом
– того измерения, если при любом 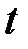 имеет место тождество:
имеет место тождество: 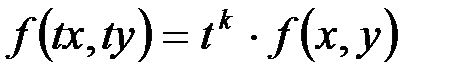 .
.
Например, 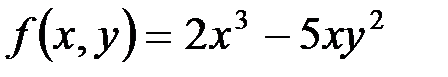 – однородная функция третьего измерения, так как
– однородная функция третьего измерения, так как 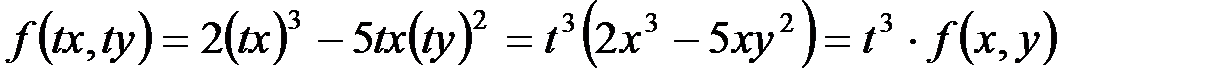 .
.
Аналогично доказывается, что функции
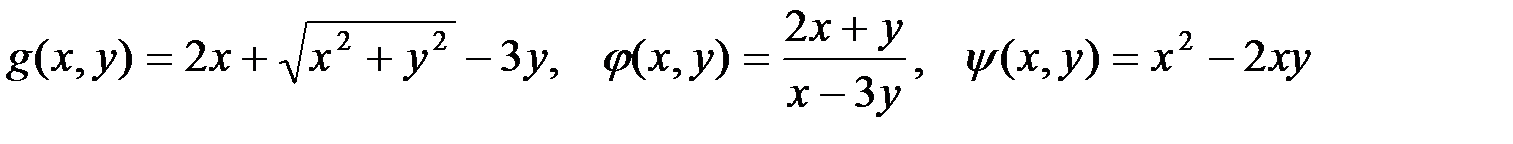
являются однородными функциями соответственно первого, нулевого и второго измерений.
Дифференциальное уравнение первого порядка вида: 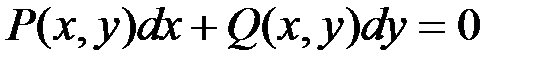
называется однородным, если  и
и 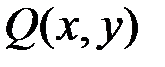 – однородные функции одинакового измерения.
– однородные функции одинакового измерения.
Однородное дифференциальное уравнение приводится к дифференциальному уравнению с разделяющимися переменными подстановкой 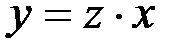 , где
, где 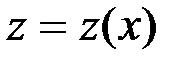 – новая неизвестная функция.
– новая неизвестная функция.
Пример 9
Решить уравнение:
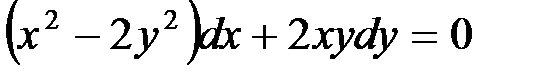 .
.
Решение
В данном уравнении функции 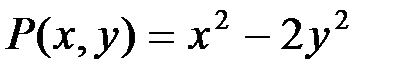 ,
, 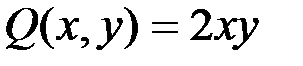 – однородные второго измерения, следовательно, уравнение является однородным.
– однородные второго измерения, следовательно, уравнение является однородным.
Положим 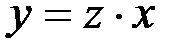 , откуда
, откуда 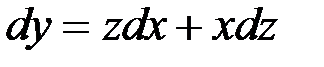 . Подставляем эти выражения
. Подставляем эти выражения 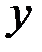 и
и 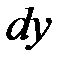 в данное уравнение:
в данное уравнение:
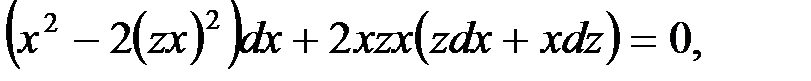
т.е.
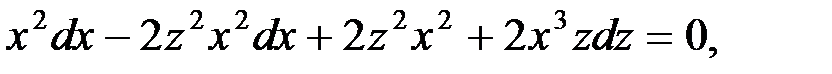
или
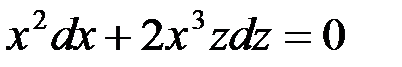 .
.
Выражение, содержащее dz, всегда оставляем в левой части уравнения, а все остальное переносим в правую часть:
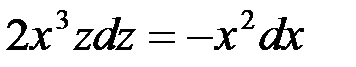 .
.
Разделим обе части равенства на 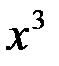 , получим:
, получим:
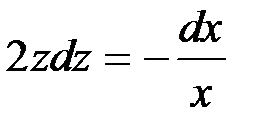 .
.
Проинтегрируем обе части последнего равенства:
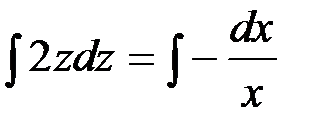 ,
,
откуда
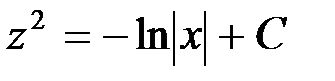 ,
,
или
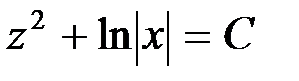 .
.
Возвращаясь к прежней функции  , находим общее решение дифференциального уравнения:
, находим общее решение дифференциального уравнения: 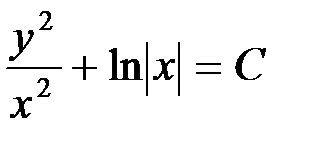 .
.
Пример 10
Найти частное решение уравнения: 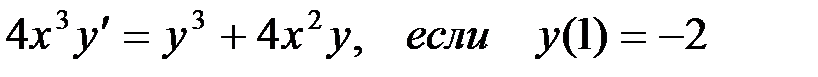
Решение
Воспользовавшись тем, что 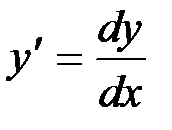 , имеем:
, имеем:
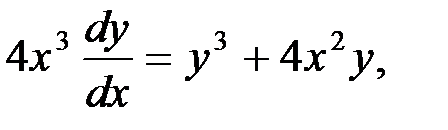
или 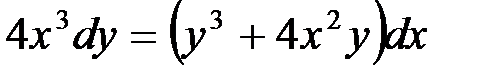 .
.
|
|
|
Полученное уравнение является однородным. Положим 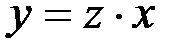 , откуда
, откуда 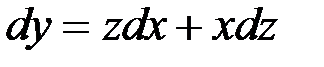 . Подставляя эти выражения
. Подставляя эти выражения 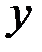 и
и 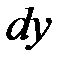 в данное уравнение, имеем:
в данное уравнение, имеем:
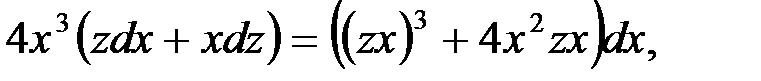
Или 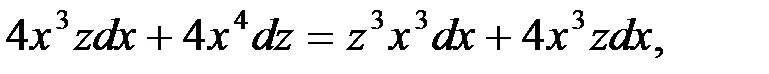
Или 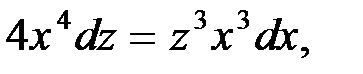
Разделим обе части равенства на выражение 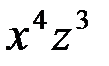 , получим:
, получим:
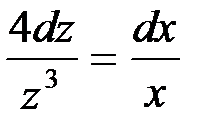 .
.
Проинтегрируем обе части последнего равенства:
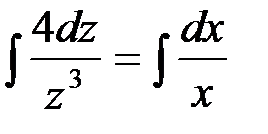 ,
,
Откуда 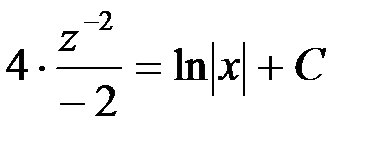
Или 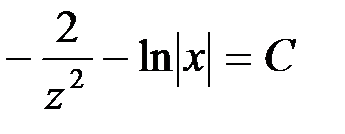 ,
,
Или 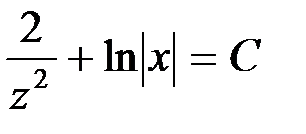 .
.
Возвращаясь к прежней функции 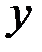 , находим общее решение дифференциального уравнения:
, находим общее решение дифференциального уравнения: 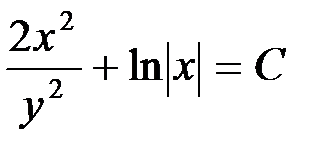 .
.
Для нахождения частного решения данного дифференциального уравнения подставим начальные значения 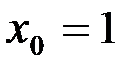 ,
, 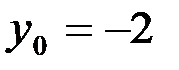 в общее решение и найдем значение
в общее решение и найдем значение 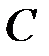 :
:
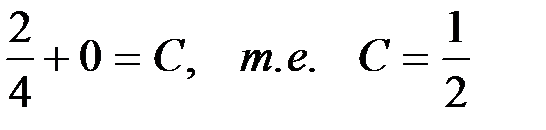 .
.
Следовательно, частное решение дифференциального уравнения имеет вид:
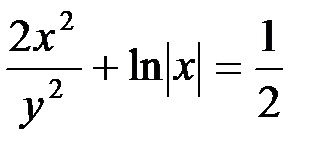
Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка вида:
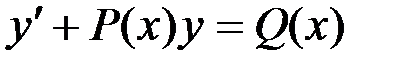 ,
,
где 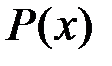 и
и 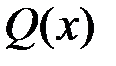 – функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка.
– функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка.
Уравнение называется линейным, так как искомая функция 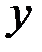 и ее производная
и ее производная 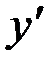 входят в это уравнение в первой степени.
входят в это уравнение в первой степени.
При решении линейных уравнений применяют метод Бернулли. Для этого используют подстановку 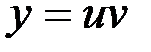 , в результате которой уравнение
, в результате которой уравнение 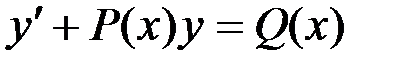 сводится к двум уравнениям с разделяющимися переменными:
сводится к двум уравнениям с разделяющимися переменными:
|
|
|
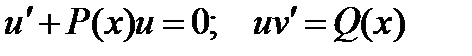
где 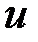 и
и 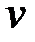 – новые функции переменной x.
– новые функции переменной x.
Алгоритм решения линейного дифференциального уравнения первого порядка
1) Привести уравнение к виду 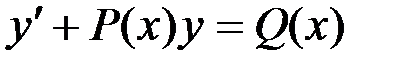 .
.
2) Используя подстановку 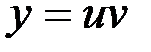 , найти
, найти 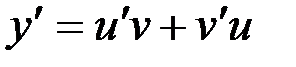 и подставить эти выражения в уравнения.
и подставить эти выражения в уравнения.
3) Сгруппировать члены уравнения и вынести одну из функций 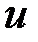 или
или 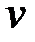 за скобки. Найти вторую функцию, приравняв выражение в скобках к нулю и решив полученное уравнение.
за скобки. Найти вторую функцию, приравняв выражение в скобках к нулю и решив полученное уравнение.
4) Подставить найденную функцию в оставшееся выражение и найти вторую функцию.
5) Записать общее решение, подставив выражения для найденных функций 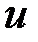 и
и 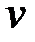 в равенство
в равенство 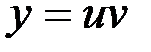 .
.
6) Если требуется найти частное решение, то определить С из начальных условий и подставить в общее решение.
Пример 11
Решить уравнение: 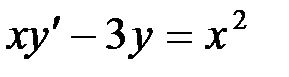 .
.
Решение
Разделим обе части уравнения на 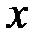 :
:
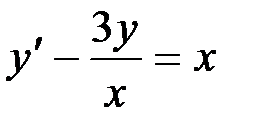 .
.
Полученное уравнение является линейным. Положим 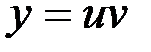 ;
; 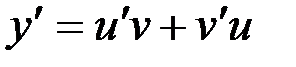 . Подставляя выражения
. Подставляя выражения 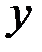 и
и 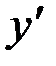 в исходное уравнение, имеем:
в исходное уравнение, имеем:
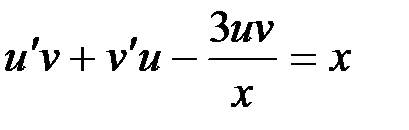 .
.
Вынесем функцию 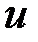 за скобки:
за скобки:
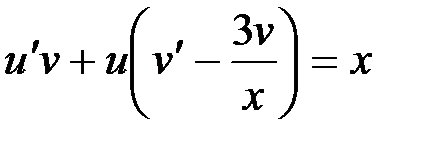 .
.
Получаем систему двух уравнений с разделяющимися переменными:
|
|
|
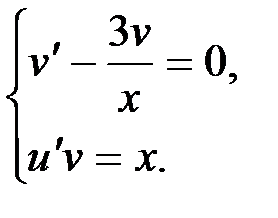
Решим первое уравнение системы:
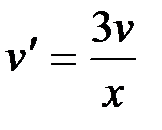 ,
,
или
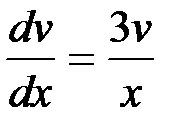 ,
,
или
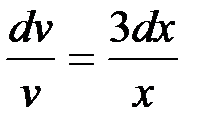 .
.
Интегрируя обе части последнего равенства, получим:
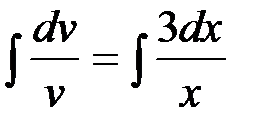
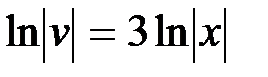 ,
,
или
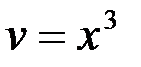 .
.
При нахождении функции 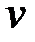 постоянная
постоянная 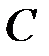 считается равной нулю. Найденное значение
считается равной нулю. Найденное значение 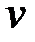 подставляем во второе уравнение системы:
подставляем во второе уравнение системы:
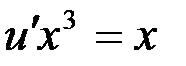 ,
,
откуда
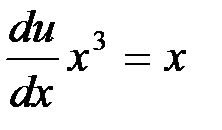 ,
,
или
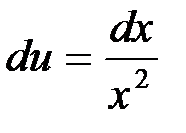 .
.
Интегрируя обе части последнего равенства, получим:
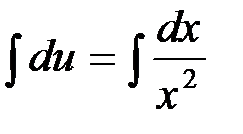 ,
,
или
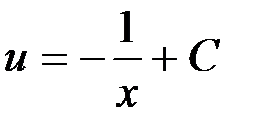 .
.
Подставляя найденные значения 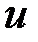 и
и 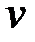 в равенство
в равенство 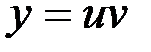 , получим общее решение данного уравнения:
, получим общее решение данного уравнения:
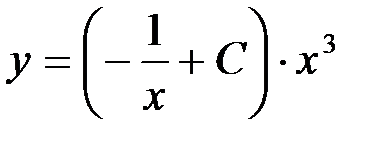
или
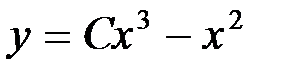 .
.
Пример 12
Найти частное решение уравнения: 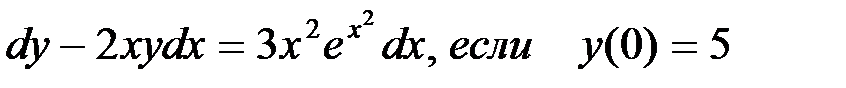 .
.
Решение Раздели мобе части уравнения на 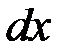
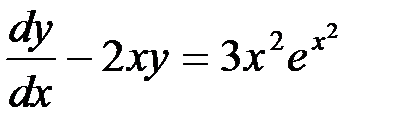 ,
,
Или 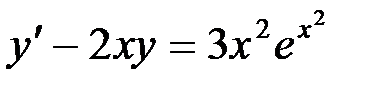 .
.
Полученное уравнение является линейным. Положим 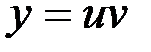 ;
; 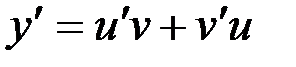 .
.
Подставляя 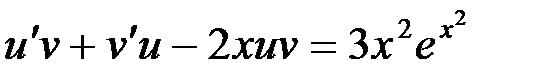 .
.
Вынесем функцию 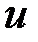 за скобки:
за скобки: 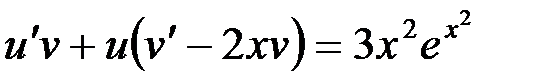 .
.
Получаем систему двух уравнений с разделяющимися переменными:
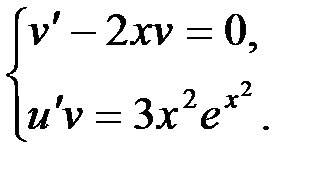
Решим первое уравнение системы: 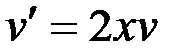 ,
,
Или 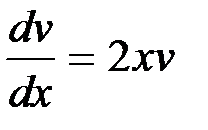 ,
,
Или 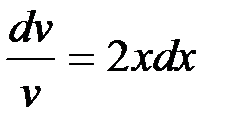 .
.
Интегрируя обе части последнего равенства, получим:
|
|
|
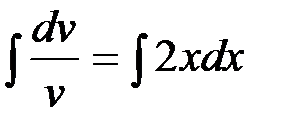 ,
,
Откуда 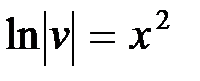 ,
,
Или 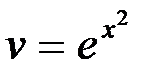
При нахождении функции 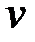 постоянная
постоянная 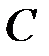 считается равной нулю. Найденное значение
считается равной нулю. Найденное значение 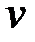 подставляем во второе уравнение системы:
подставляем во второе уравнение системы: 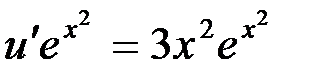
Откуда 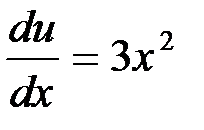 ,
,
Или 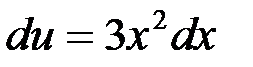 .
.
Интегрируя обе части последнего равенства, получим: 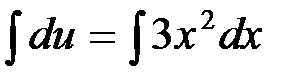 ,
,
Или 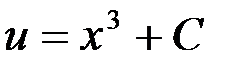 .
.
Подставляя найденные значения 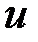 и
и 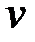 в равенство
в равенство 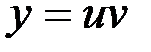 , получим общее решение данного уравнения:
, получим общее решение данного уравнения: 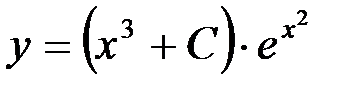
Или 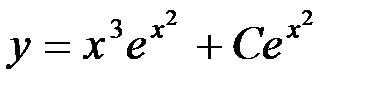 .
.
Для нахождения частного решения данного дифференциального уравнения подставим начальные значения  ,
, 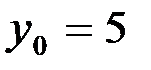 в общее решение и найдем значение
в общее решение и найдем значение 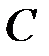 :
:
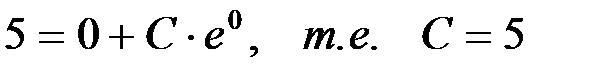 .
.
Следовательно, частное решение дифференциального уравнения имеет вид: 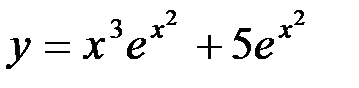 .
.
Дата добавления: 2018-05-12; просмотров: 717; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
