Решение дифференциальных уравнений первого порядка
Понятие дифференциального уравнения
Рассмотрим некоторую функцию 
. Обозначим через 
ее первую производную, через 
– вторую производную и т.д., а дифференциалы функций и аргумента обозначим соответственно dy и dx.
В дифференциальных уравнениях всегда присутствуют производные или дифференциалы функции и аргумента. Это отличительный признак дифференциального уравнения. Например,
– дифференциальные уравнения.
Наличие самой функции y и аргумента x в дифференциальном уравнении не является обязательным. Например, уравнения:
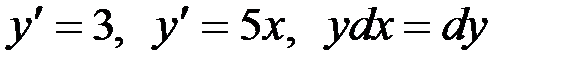
также являются дифференциальными.
Дифференциальным уравнением называется уравнение, содержащее производные искомой функции или ее дифференциалы.
Решить дифференциальное уравнение – значит найти такую функцию, при подстановке которой в данное уравнение получается верное равенство. Эта функция называется решением дифференциального уравнения.
Пример 1
Проверить, является ли функция 
решением дифференциального уравнения 
.
Решение
Находим 
. Так как 
, то получаем 
. Подставляя найденное для dy выражение в левую часть заданного уравнения, имеем 
, т.е. данная функция есть решение этого уравнения.
Пример 2
Какие из перечисленных ниже функций представляют собой решения дифференциального уравнения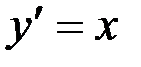 
:
.
Решение
Функции 
есть решения дифференциального уравнения 
, так как подстановка этих функций в данное уравнение обращает его в верное равенство. Остальные функции не являются решениями этого уравнения.
|
|
|
Решение, содержащее постоянную С, называется общим решением дифференциального уравнения.
В примере 2 
– общее решение уравнения 
.
Решение, в которое подставлено числовое значение С, называется частным решением дифференциального уравнения.
В примере 2 
– частное решение уравнения .
Пример 3
Функция 
является общим решением дифференциального уравнения 
. Найти частное решение уравнения, если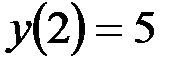 
.
Решение
Подставим в общее решение заданные начальные условия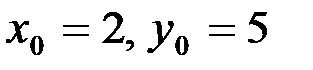 
, получим 
, откуда 
.
Теперь подставим значение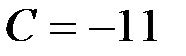 
в общее решение и найдем искомое частное решение 
.
Таким образом, при решении дифференциального уравнения сначала получается общее решение. Затем, если известны начальные данные, то можно получить частное решение.
Чтобы найти частное решение дифференциального уравнения по заданным начальным условиям, необходимо:
1) подставить начальные условия в общее решение и вычислить С;
2) полученное числовое значение С подставить в общее решение.
Задача отыскания конкретного частного решения данного дифференциального уравнения по начальным условиям называется задачей Коши.
|
|
|
Дата добавления: 2018-05-12; просмотров: 1504; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!