Примеры вычисления предела функции в точке
Пример 4
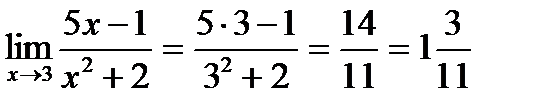
Пример 5
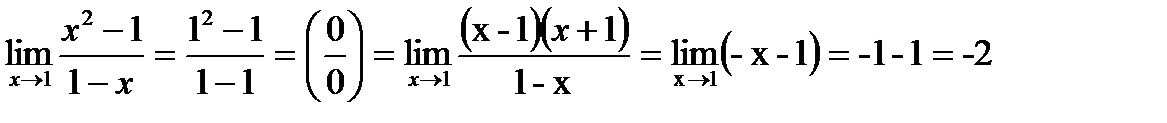
Пример 6
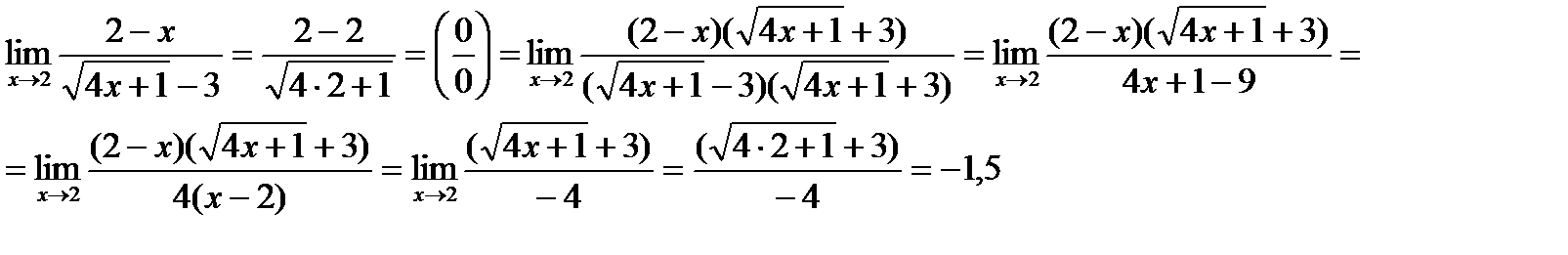
В примере 4 вычислили предел непосредственной подстановкой х = 3. В примере 5 для раскрытия неопределенности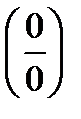 
применили формулу сокращенного умножения. В примере 6 для раскрытия неопределенности 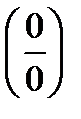числитель и знаменатель дроби умножили на выражение, сопряженное знаменателю.
Замечательные пределы
| 
|
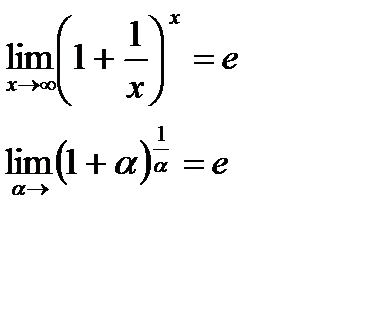
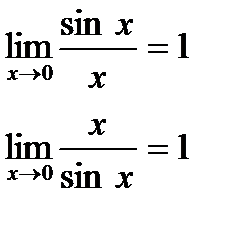
Примеры вычисления замечательных пределов
Пример 1
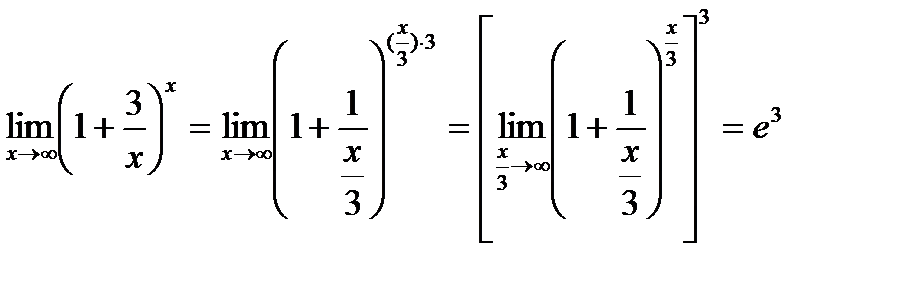
Пример 2
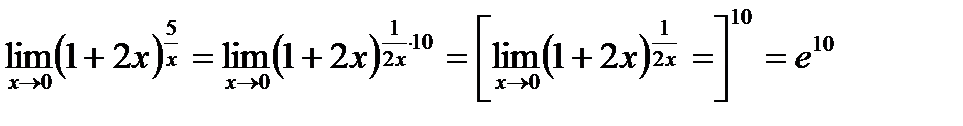
Пример 3
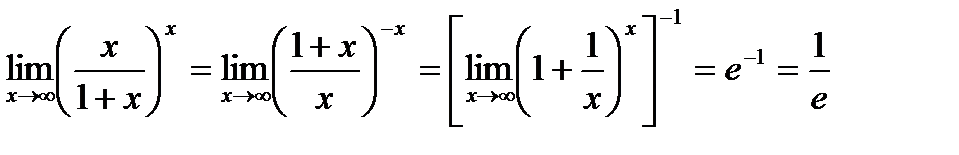
Пример 4
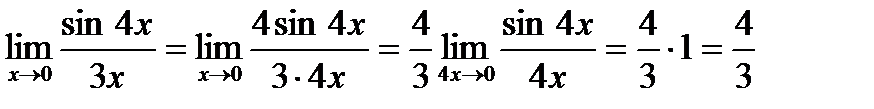
Пример 5
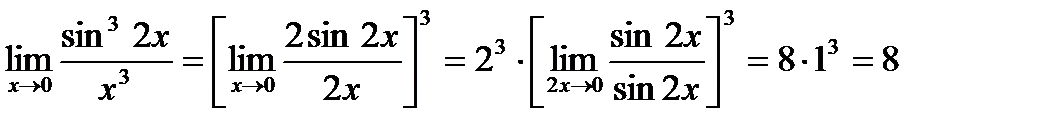
Вычисление производной.
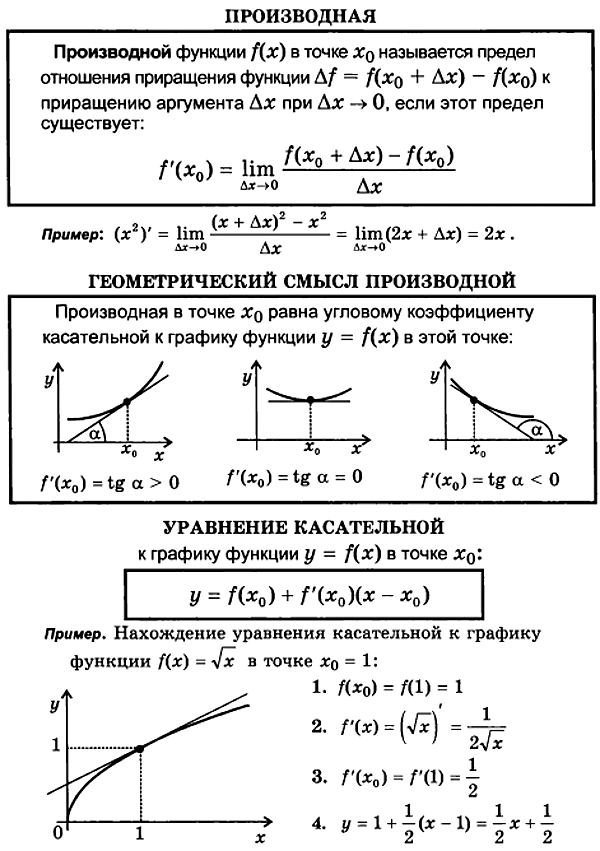
Правила вычисления производных
u и v - функции
u' и v' - производные
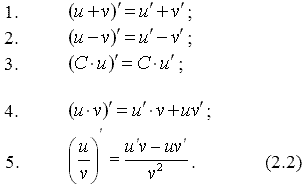
Основные формулы (таблица производных)
| 
|
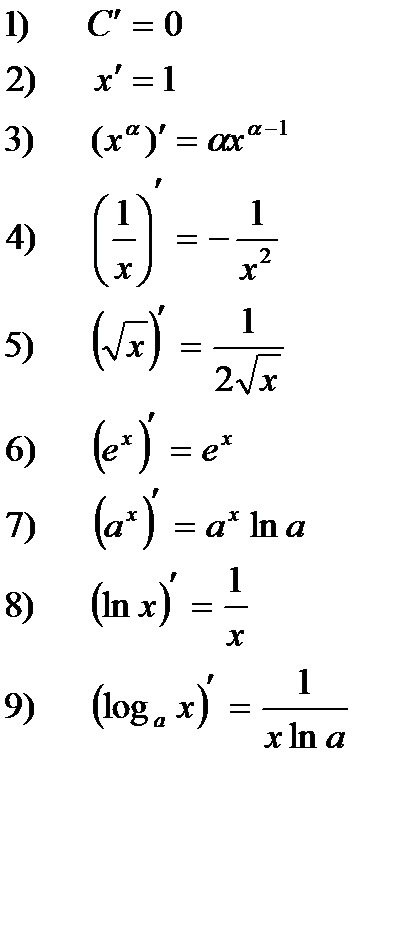
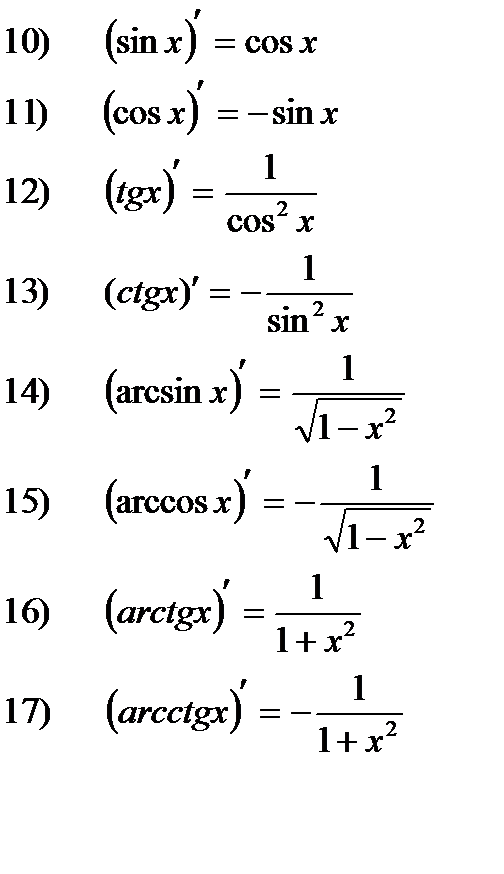
Найти производные функций
1. 
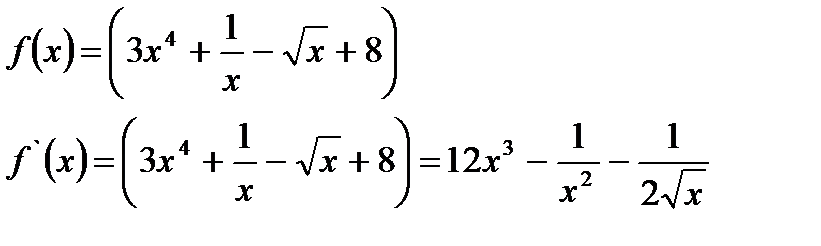
2. 
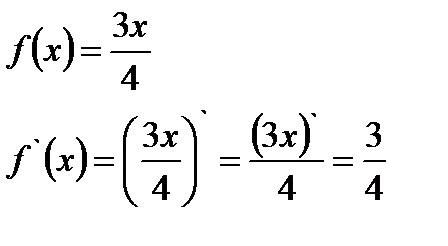
3. 
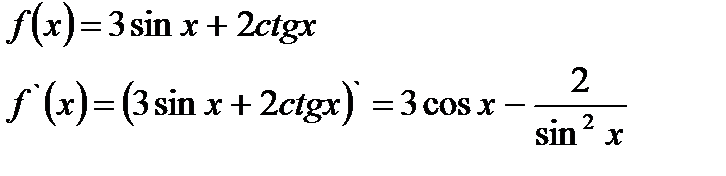
4. 
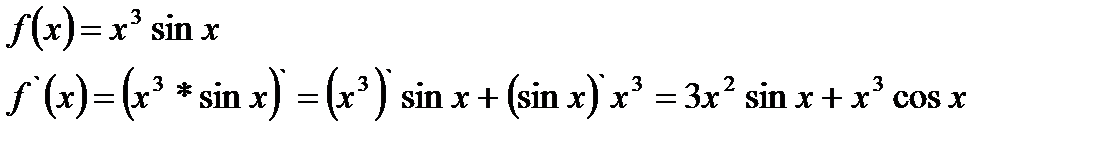
5. 
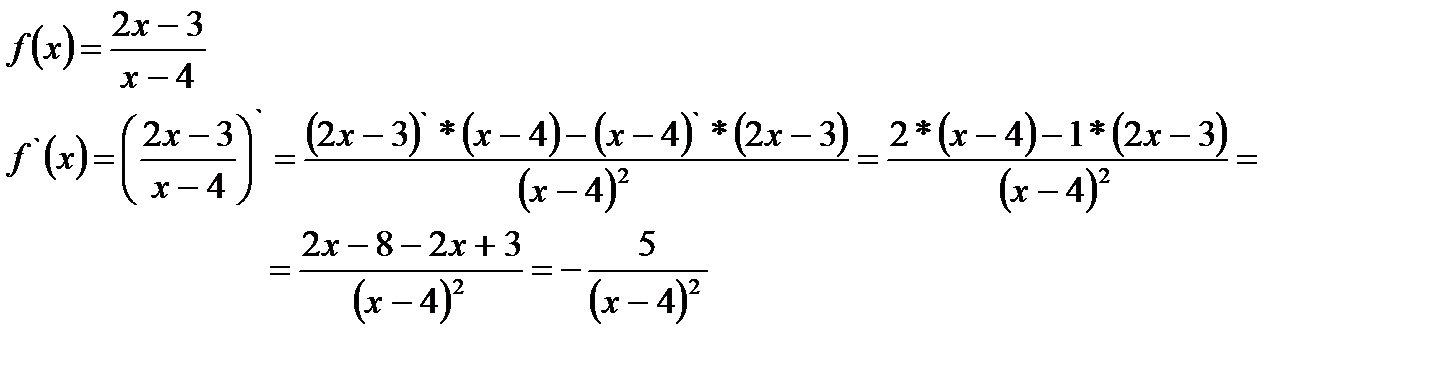
Интегрирование
Неопределенный интеграл
Вычислить неопределённый интеграл означает восстановить функцию по известной производной этой функции. Восстановленная таким образом функцияF(x) называется первообразной для функции f(x).
Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
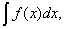
где знак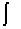 
называется знаком интеграла,
функция f(x) – подынтегральной функцией,
аf(x)dx – подынтегральным выражением.
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
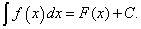
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Теорема.Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C, где С– произвольная постоянная.
|
|
|
Свойства неопределённого интеграла
Теорема 1.Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Теорема 2.Неопределённый интеграл от дифференциала функции f(x) равен функцииf(x) с точностью до постоянного слагаемого, т.е.
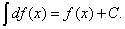(3)
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Теорема 3.Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
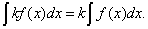(4)
Теорема 4.Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
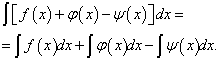
ТАБЛИЦА ИНТЕГРАЛОВ
1) 
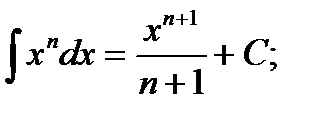
2) 
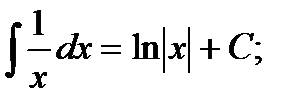
3) 
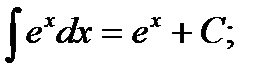
4) 
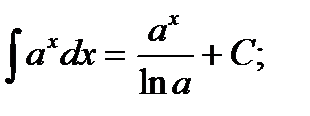
5) 
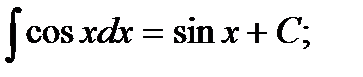
6) 
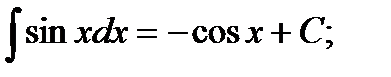
7) 
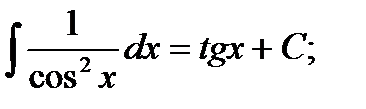
8) 
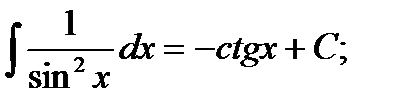
9) 
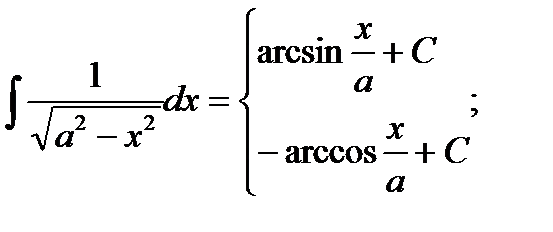
10) 
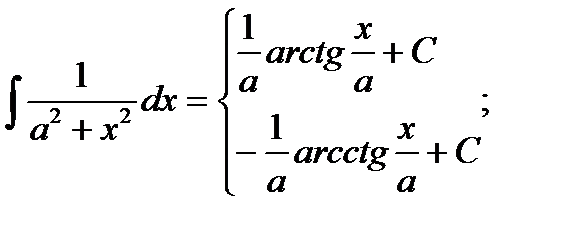
11) 
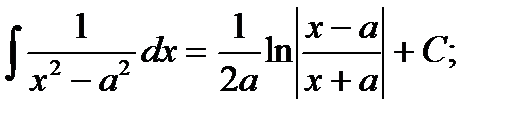
12) 
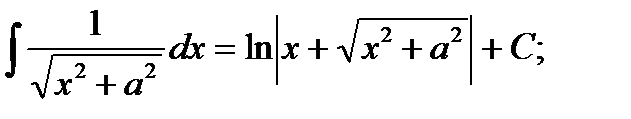
13) 
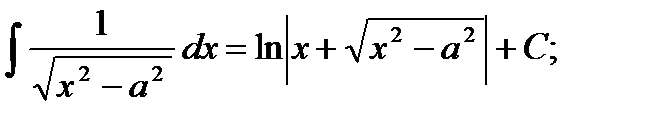
14) 
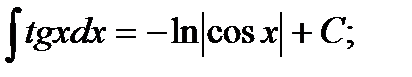
15) 
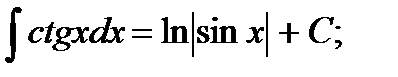
16) 
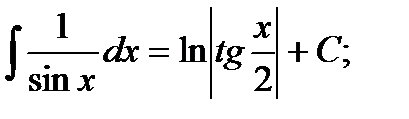
17) 
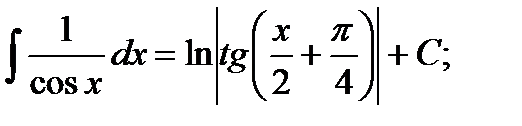
18) 
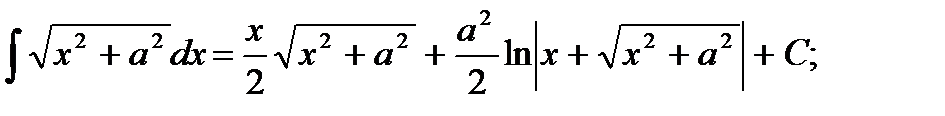
19) 
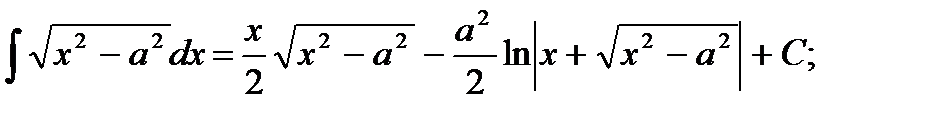
20) 
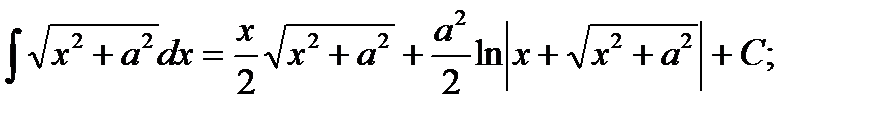
1 Интегрирование подстановкой
Теорема: Пусть функция t=j(x) определена и дифференцируема на промежутке х , а промежуток Т – множество её значений. Пусть функция у=f(t) определена на Т и имеет на этом промежутке первообразную F(t). Тогда на промежутке х функция F(j(x)) является первообразной для функции f(j(x))×j’(x), т.е.
|
|
|
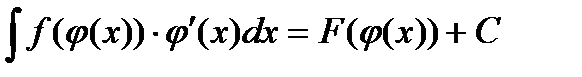
На основании этой теоремы получаем:
|
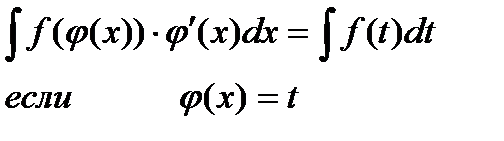
формула замены переменной в неопределённом интеграле
План интегрирования способом подстановки.
1. Определяют к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
2. Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате производят обратную замену, т. е. Переходят к старой переменной. Результат можно проверить дифференцированием.
Пример 1:
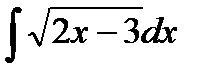
| Определяем к какому табличному интегралу приводится данный интеграл |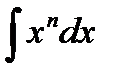 
|
| Определяем, какую часть подынтегральной функции заменить новой переменной и записываем эту замену. |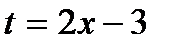 
|
| Находим дифференциалы обеих частей записи и выражаем дифференциал старой переменной через дифференциал новой переменной. |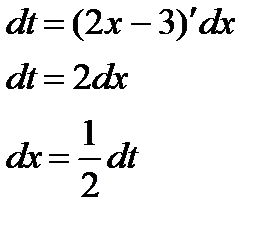 
|
| Производим замену под интегралом. |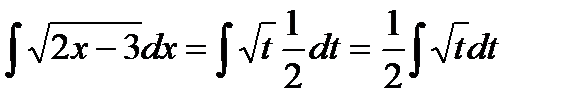 
|
| Находим полученный интеграл. |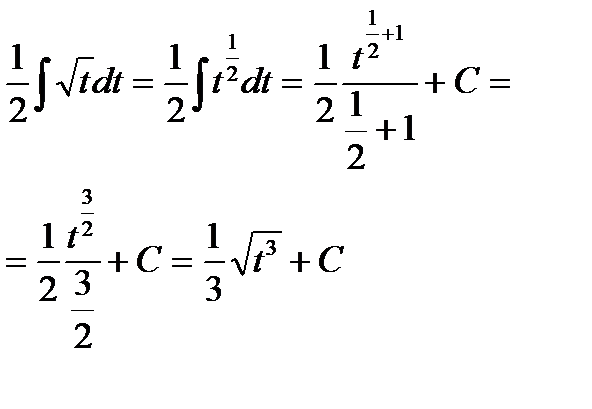 
|
| В результате производим обратную замену. |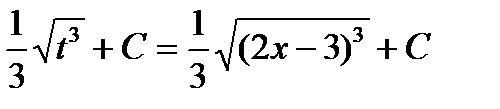 
|
Правило 1:Если подынтегральная функция имеет вид f(ax+b), то может оказаться полезной подстановка t=ax+b.
|
|
|
Пример 2:
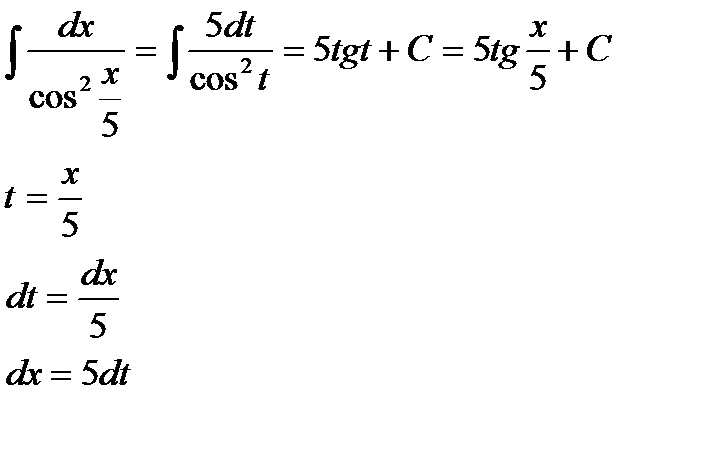
Иногда перед тем как сделать подстановку подынтегральное выражение надо преобразовать.
Пример 3:
Пример 4:
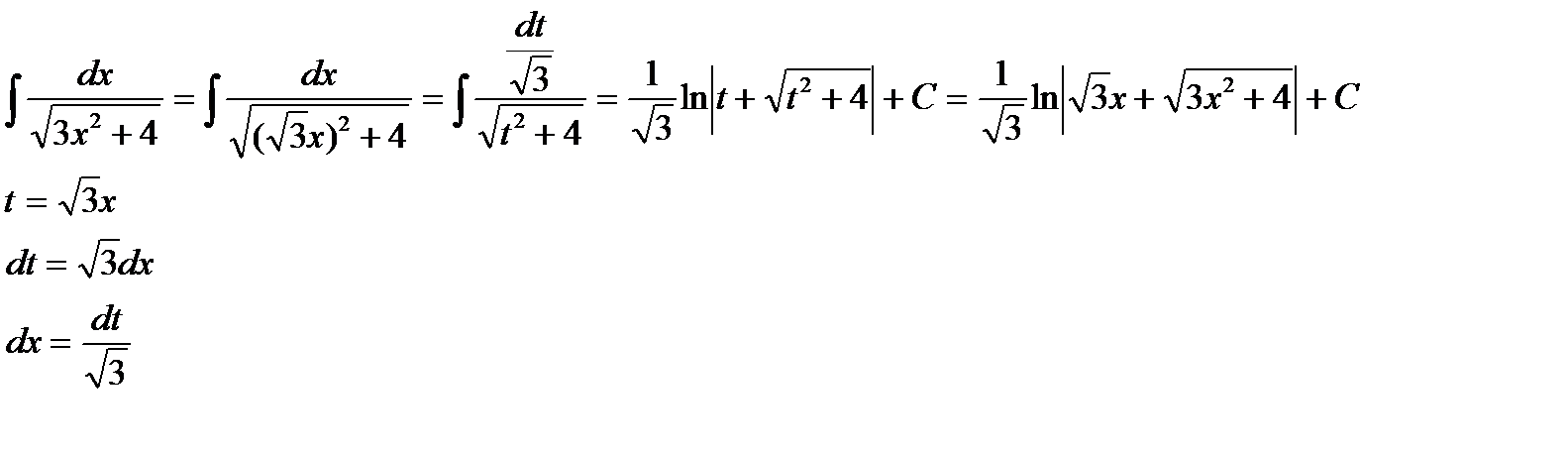
Правило 2:Пусть подынтегральное выражение разбито на два сомножителя и в одном из них легко распознать дифференциал функции j(х). Может оказаться, что после подстановки t=j(х) второй сомножитель превратиться в такую функцию от t, которую легко проинтегрировать. Тогда подстановка окажется полезной.
Пример 5:
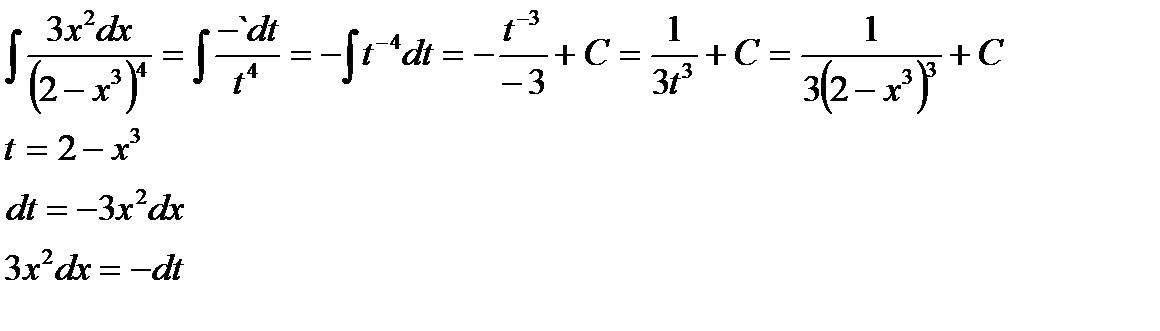
Пример 6:
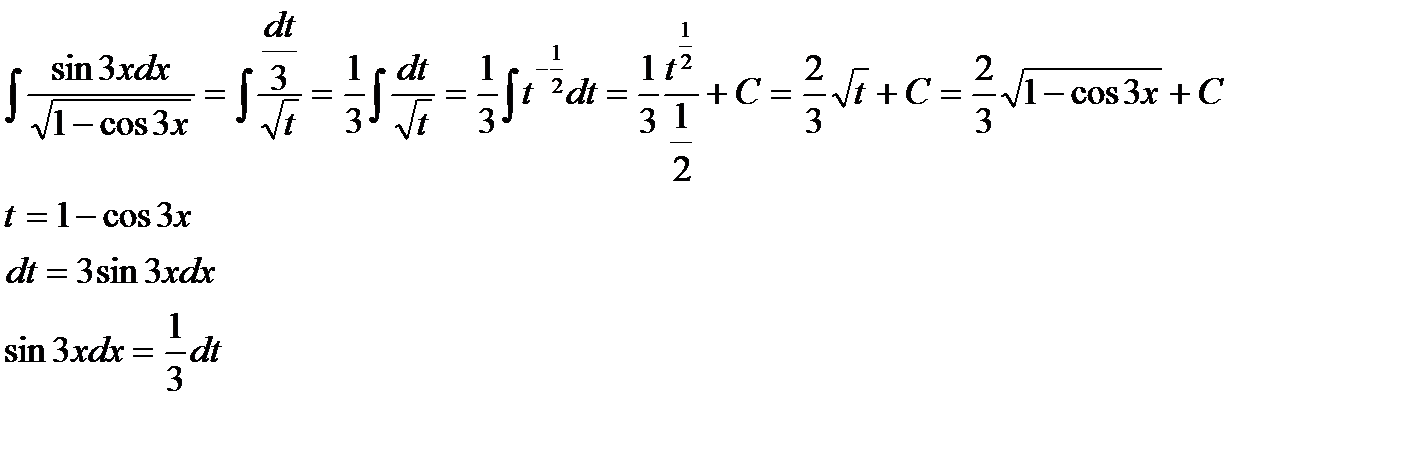
Пример 7:
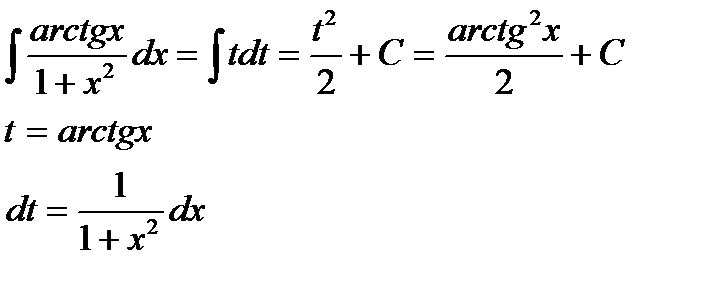
2 Интегрирование по частям
Теорема:Пусть на промежутке х функции u(x) и v(x) дифференцируемы и существует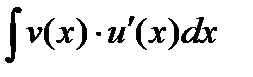 
(т.е. функция v(x)×u’(x) имеет первообразную на х), тогда 
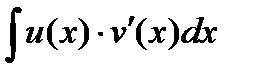также существует на х и
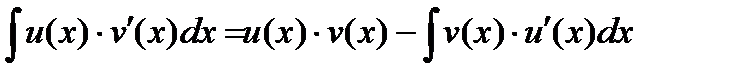
формула интегрирования по частям
В более коротком виде её записывают так:
|
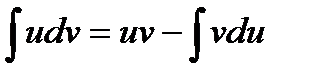
При практическом использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают u и dv. Множитель u выбирают так, чтобы u’ было проще, чем u.
|
|
|
Замечание 1:В интегралах вида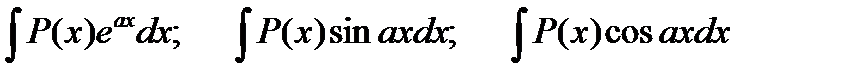 
, где Р(х) – многочлен относительно х, а - некоторое число. Полагают u=P(x), а все остальные сомножители за dv. Если Р(х) – многочлен степени выше первой, то операцию интегрирования по частям следует повторить несколько раз.
Пример 8.
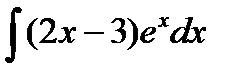
| Представим данное подынтегральное выражение в виде произведения двух сомножителей, которые обозначим u и dv. | u=2x-3 dv=exdx |
| Зная u найдём du (du=u’dx) | du=2dx |
Зная dv найдём v (v=  )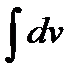
| 
|
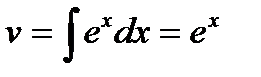
| Подставим всё в формулу интегрирования по частям ( )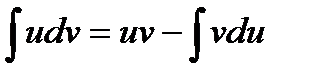
| 
|
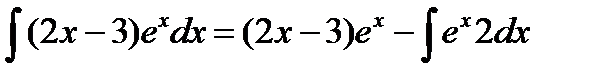
| Вычислим второй интеграл |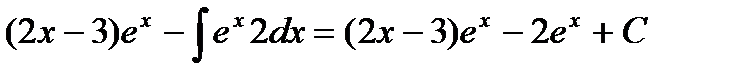 
|
Пример 9:
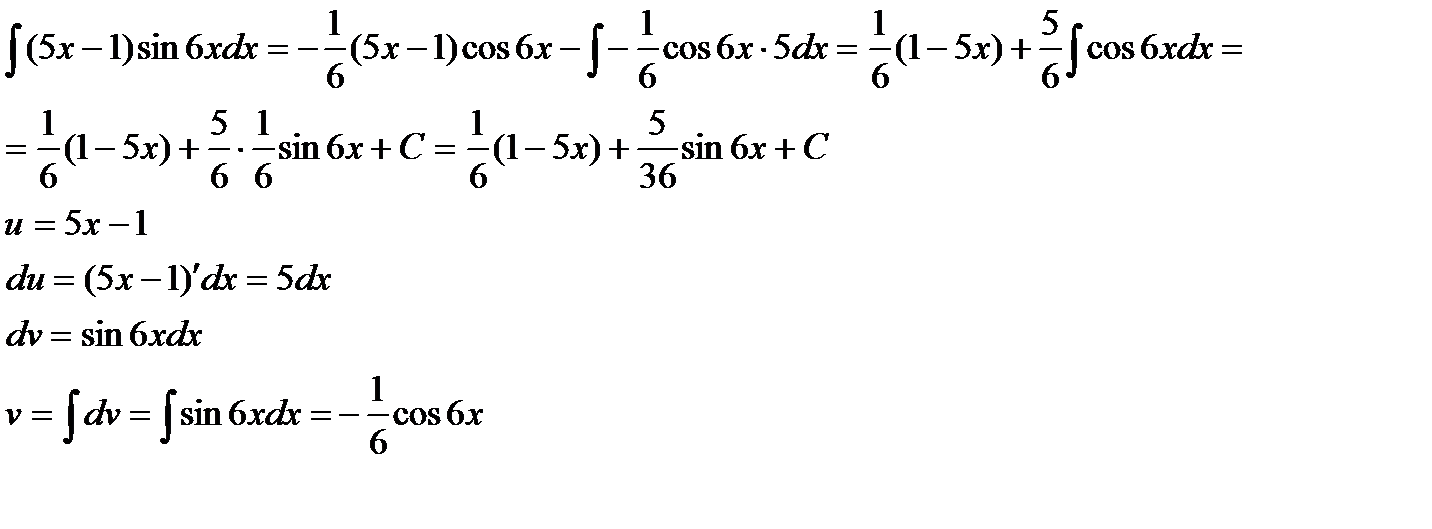
Пример 10:
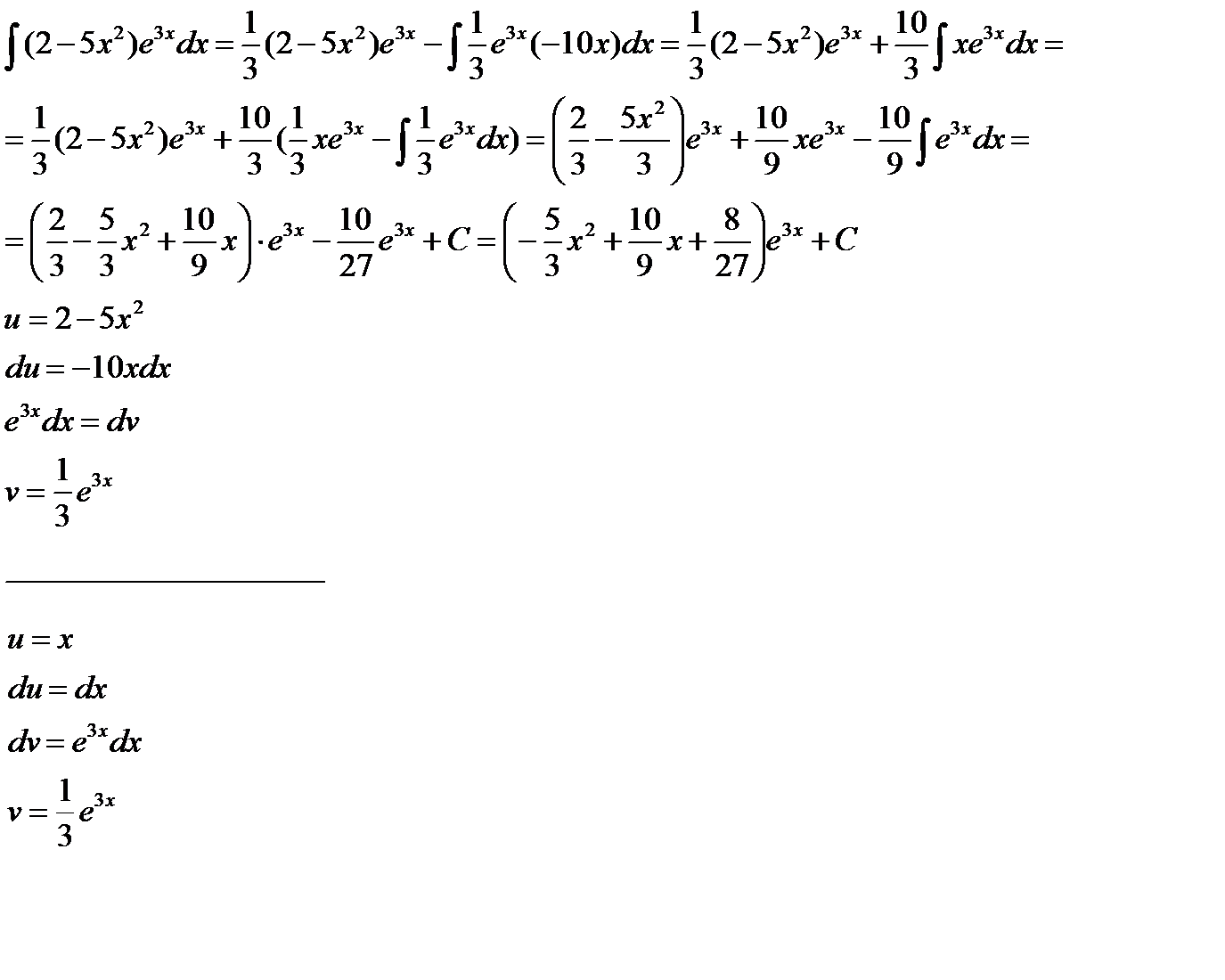
Замечание 2:В интегралах вида 
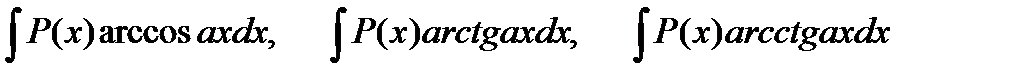полагают P(x)dx=dv, а остальные сомножители u.
Пример 11:
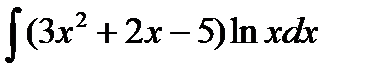
| Представим данное подынтегральное выражение в виде произведения двух сомножителей, которые обозначим u и dv. |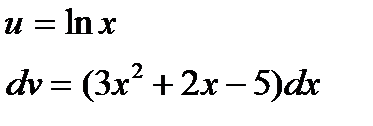 
|
| Зная u найдём du (du=u’dx) |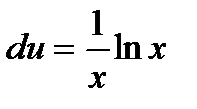 
|
| Зная dv найдём v (v= )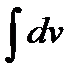
| 
|
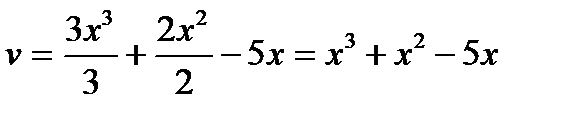
| Подставим всё в формулу интегрирования по частям ( )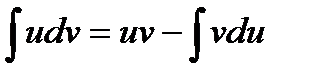
|  
|
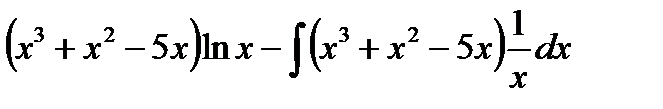
| Вычислим второй интеграл, предварительно раскрыв скобки в подынтегральном выражении |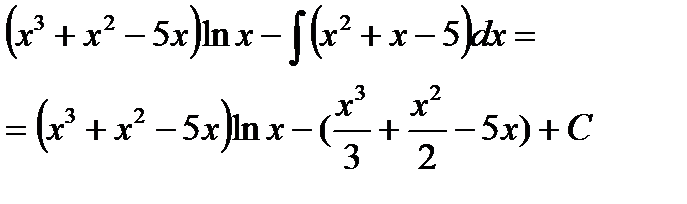 
|
Пример 12:
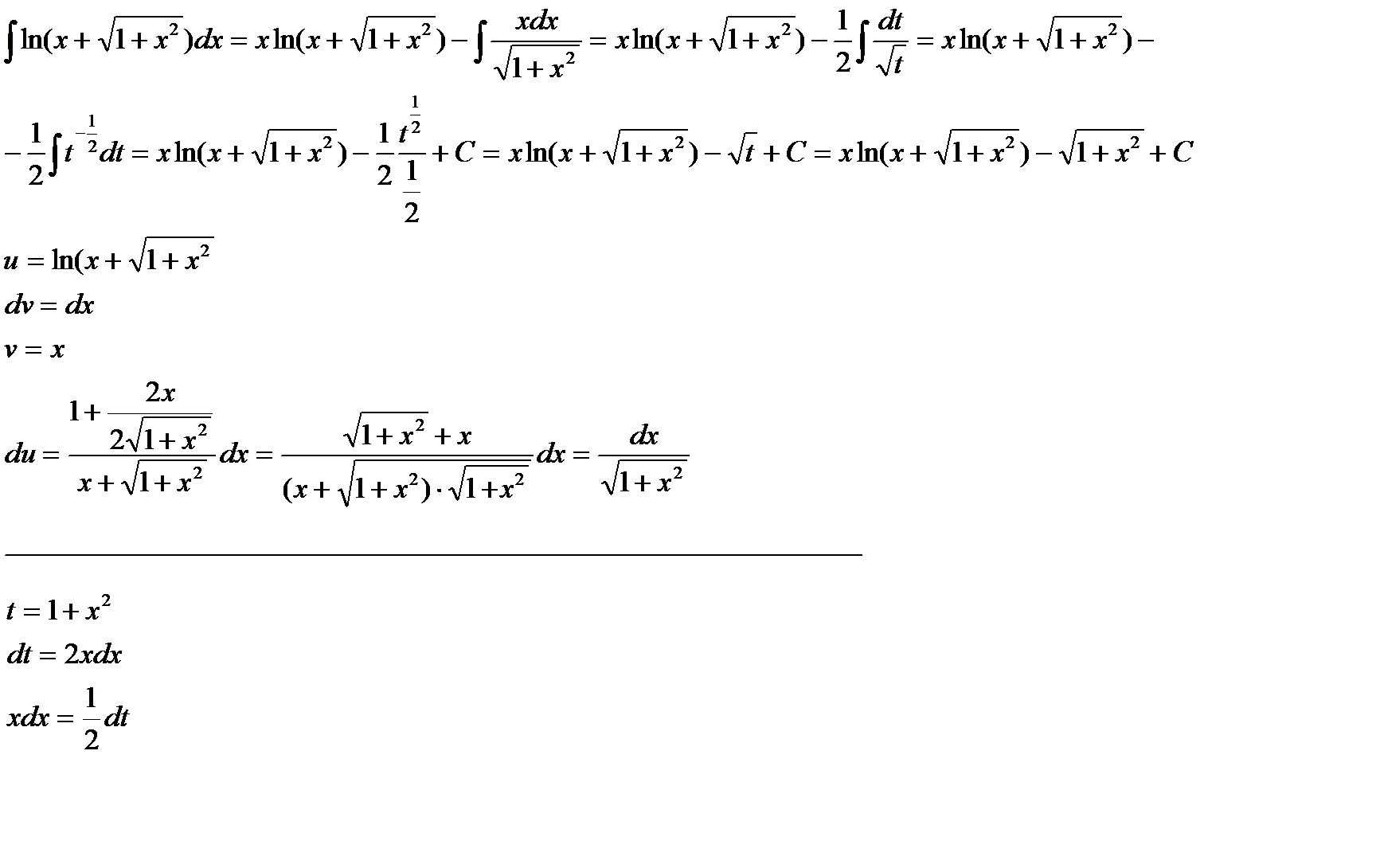
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
Дата добавления: 2018-05-12; просмотров: 997; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!