Порядок дифференциального уравнения
Дифференциальные уравнения принято классифицировать в зависимости от порядка производной, входящей в уравнение.
Наивысший порядок производной, входящий в уравнение, называется порядком дифференциального уравнения. Например,
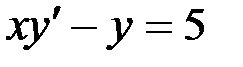– дифференциальное уравнение первого порядка;
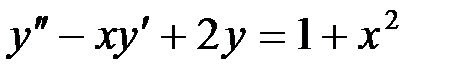– дифференциальное уравнение второго порядка;
– дифференциальное уравнение третьего порядка.
К дифференциальным уравнениям первого порядка относятся уравнения, в которые входят производные (или дифференциалы) не выше первого порядка.
Общий вид дифференциального уравнения первого порядка таков:
Если это уравнение можно разрешить относительно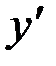 
, то оно примет вид:
Дифференциальные уравнения первого порядка с разделенными переменными
Уравнение вида: 
(1)
где 
– данные функции, называется уравнением с разделенными переменными.
Это уравнение можно переписать в виде: 
Решение таких уравнений выполняется непосредственным интегрированием.
Пример 4
Решить уравнение:
Решение
Выражение, содержащее dy, всегда оставляем в левой части уравнения, а все остальные выражения переносим в правую часть:
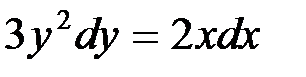
Интегрируя обе части полученного уравнения, имеем:
,
отсюда
.
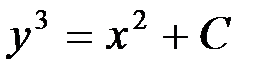Это общее решение дифференциального уравнения можно записать так:
|
|
|
.
Пример 5
Найти частное решение уравнения:
.
Решение
Выражение
оставляем в левой части, а все остальное переносим в правую часть:
.
Интегрируя обе части полученного уравнения, имеем:
,
отсюда
.
Найденное общее решение дифференциального уравнения запишем в виде:
.
подставим начальные значения 
, 
в общее решение и найдем значение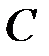 
:
.
Следовательно, частное решение дифференциального уравнения имеет вид 
.
Дифференциальные уравнения первого порядка с разделяющимися переменными
Уравнение вида: 
(2)
где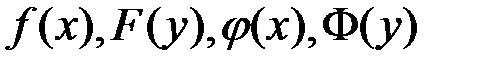 
– данные функции, называется уравнением с разделяющимися переменными.
Уравнение (2) можно привести к виду (1), если разделить все его члены на произведение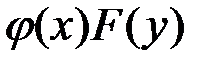 
.
Алгоритм решения дифференциального уравнения с разделяющимися переменными
1) Выразить производную функции через дифференциалы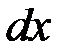 
и 
.
2) Члены с одинаковыми дифференциалами перенести в одну сторону равенства и вынести дифференциал за скобку.
3) Разделить переменные.
4) Проинтегрировать обе части равенства и найти общее решение.
5) Если заданы начальные условия, то найти частное решение.
|
|
|
В зависимости от вида уравнения некоторые пункты алгоритма решения могут быть опущены.
Пример 6
Решить уравнение:
.
Решение
Разделим обе части равенства на выражение 
:
.
Интегрируя обе части равенства, имеем:
; 
;
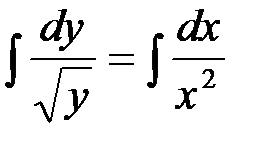откуда получаем общее решение 
.
Пример 7
Решить уравнение:
.
Решение
Заменим 
на 
, получим:
.
Умножим обе части равенства на выражение 
:
.
Интегрируя обе части равенства, имеем:
;
откуда
.
Общее решение дифференциального уравнения имеет вид:
.
Пример 8
Найти частное решение уравнения:
Решение
Разделим обе части равенства на выражение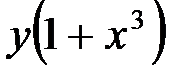 
:
.
Интегрируя обе части равенства, имеем:
,
откуда
,
или
.
Так как произвольная постоянная 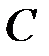может принимать любые числовые значения, то для удобства дальнейших преобразований вместо 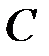напишем 
:
.
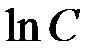Тогда общее решение уравнения имеет вид:
.
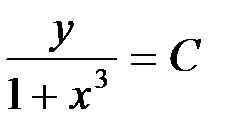Для нахождения частного решения данного дифференциального уравнения подставим начальные значения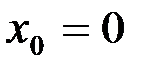 
, 
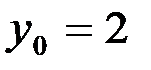в общее решение и найдем значение :
.
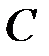Следовательно, частное решение дифференциального уравнения имеет вид:
.
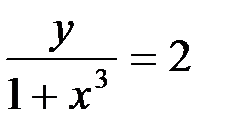Дата добавления: 2018-05-12; просмотров: 389; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!