Алгебраические критерии устойчивости.
Рисунок 48
|
Исходя из расположения на комплексной плоскости, корни с отрицательными вещественными частями называются левыми, с положительными - правыми (рисунок 48). Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю, а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости.
Таким образом, исследование устойчивости системы сводится к определению знаков вещественных частей корней характеристического уравнения системы. Но решение уравнений четвертой и более высоких степеней может встречать затруднения. Поэтому применяются косвенные методы анализа устойчивости без определения корней характеристического уравнения, по определенным критериям устойчивости.
Необходимое условие устойчивости. Если все корни характеристического уравнения левые (вещественные части всех корней отрицательны), то все коэффициенты уравнения имеют один знак, т.е. все значения 
либо больше нуля, либо меньше нуля одновременно. Равенство коэффициентов нулю не допускается (граница устойчивости). Доказательство очень простое и заключается в разложении полинома на простейшие множители. Они могут быть вещественные или комплексно - сопряжённые. Объединим последние в пары и перемножим, при этом в скобках нет ни одного отрицательного числа, а, следовательно, знак всех членов характеристического уравнения будет определяться знаком коэффициента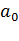 
. В дальнейшем будем рассматривать только уравнения, где 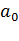> 0. В противном случае уравнение умножается на -1.
|
|
|
Рассмотренное условие при порядке системы больше 2 является необходимым, но не достаточным условием, и применяется для отсеивания заведомо неустойчивых систем. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
Критерий Гурвица. Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица D по алгоритму:
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от 
до ;
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.
|
|
|
Чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и все n главных диагональных миноров матрицы Гурвица были положительны. Число определителей Гурвица равно порядку характеристического уравнения п.
Критерий Гурвица применяют при n ≤ 5. При больших порядках возрастает число определителей, и процесс становится трудоемким. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ.
Емкость – это способность объекта накапливать рабочее вещество или энергию, участвующую в рабочем процессе при условии, что в объекте регулирования имеется сопротивление выходу этого вещества или энергии.
Примеры: 1. Если бы не было гидравлического сопротивления сливных труб объекта регулирования (водонапорного бака), в котором регулируется уровень, то жидкость не могла бы накапливаться, и сосуд не обладал бы емкостью.
2. Если тепловой объект (холодильная камера), в котором регулируется температура, не имел бы тепловой изоляции, то тепловая емкость не создавалась бы вследствие мгновенного рассеивания всего тепла.
Пояснение. Емкость объекта также принято называть его аккумулирующей способностью. О количестве аккумулированного в объекте рабочего вещества или энергии можно судить по значению регулируемой величины (уровню, температуры, давлению и др.), которая характеризует ее запас в объекте. В зависимости от физической природы регулируемого процесса, объекты подразделяются на гидравлические, механические, тепловые и пневматические аккумуляторы.
|
|
|
Гидравлическими аккумуляторами являются различные резервуары: цистерны и расходные баки масла, воды; паровые котлы. При прочих равных условиях аккумулирующая способность огнетрубного котла выше, чем воздушного подогревателя (рекуператора) водотрубного.
Механическими аккумуляторами являются подвижные части машин, аккумулирующих кинетическую энергию вращения. К ним относятся – коленчатый вал двигателя; ротор турбины; валы различных вспомогательных механизмов.
Тепловыми аккумуляторами являются части теплообменных аппаратов: зарубашечное пространство компрессора; масляные и водяные холодильники; подогреватели топлива и др. В процессе накапливания энергии участвуют металл теплообменного аппарата и жидкость, находящаяся в нем.
Пневматическими аккумуляторами являются пусковые баллоны, ресиверы, участки паровых и воздушных магистралей.
|
|
|
В приведенных четырех типах аккумуляторов регулируемыми параметрами соответственно являются: уровень, частота вращения, температура и давление.
При наличии разности значений между притоком и оттоком рабочего тела, регулируемый параметр изменяется со скоростью, зависящей от емкости объекта. Чем меньше емкость объекта, тем выше скорость изменения регулируемой величины и тем сложнее ее регулировать.
Рисунок 47
Скорость изменения регулируемой величины, в данном случае температуры, при одинаковом возмущении на объекты с различной емкостью, приведена на рисунке 47.
Постоянная времени – это время, в течение которого объект при внесении скачкообразного возмущения переходит из одного равновесного (установившегося) состояния в другое при условии, что скорость изменения регулируемой величины будет постоянной и соответствовать максимальному начальному значению.
Для объекта 1, постоянная времени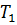 
определяется интервалом времени 
, по касательной а.
Время переходного процесса 
, это время завершения переходного процесса из одного установившегося состояния объекта в другое, и в среднем оно составляет =(3…4)Т.
Вывод: из переходных характеристик видно (рисунок 47), что объект 2 имеет большую постоянную времени, чем объект 1, т.е. 
и 
следовательно, он имеет и большую емкость. Чем больше постоянная времени, тем меньше скорость изменения внутренних параметров объекта подлежащих регулированию, а значит, что его проще автоматизировать.В зависимости от числа емкостей, объекты подразделяются на одно, двух и многоемкостные.
Одноемкостной объект. Такие объекты регулирования имеют две входные величины (нагрузку N и регулирующее воздействие 
) и одну выходную – усредненную регулируемую величину у.
Самовыравнивание— такое свойство объектов регулирования, в силу которого при изменении нагрузки объекта (притока или стока) значение регулируемого параметра стремится без участия регулятора к новому установившемуся значению, соответствующему новой измененной нагрузке объекта. Большая степень самовыравнивания способствует более быстрой стабилизации регулируемой величины и этим облегчает процесс регулирования. Некоторые объекты практически не обладают способностью самовыравнивания. Другие из-за большой степени самовыравнивания могут не требовать автоматического регулирования.
Таким образом, самовыравниванием называют свойство устойчивого объекта самостоятельно устанавливаться в равновесное состояние после изменения своей входной величины. На рисунках 48 и 49 представлены характеристики объекта одноемкостного (рисунок 48а) и многоемкостного (рисунок 48б) без самовыравнивания.
Рисунок 48
Характеристика объекта одноемкостного (рисунок 49а) и многоемкостного (рисунок 49б) с самовыравниванием.
Рисунок 49
Запаздывание
Большинство технологических объектов характеризуется наличием чистого запаздывания в каналах регулирования. Запаздывание, возникающее при протекании потока вещества по длинным трубопроводам, носит название транспортного запаздывания. Запаздывание возможно и в результате использования в системе регулирования периодически действующих приборов или регуляторов – таких, как газовый хроматограф или цифровая вычислительная машина, включенная в цепь обратной связи.
Рисунок 50
На рисунке 50 представлены переходные функции многоемкостных объектов (1) и их аппроксимация (2) одноемкостным (а) или двухъемкостным (б) звеном с приведенным запаздыванием τ: Т — постоянная времени.
Многоемкостной объект с близкими по величине постоянными времени (например, тарельчатые аппараты) или объект с распределенными параметрами (трубчатые или насадочные аппараты) характеризуется переходными функциями с затянутым начальным участком (рисунок 50), когда выходная координата практически не изменяется. В этом случае говорят о приведенном (эффективном) запаздывании, которое находят путем аппроксимации объекта одно- или двухъемкостным звеном с чистым запаздыванием.
Из-за значительного чистого запаздывания в объекте автоматизации существенно снижается качество регулирования при использовании обычных промышленных регуляторов.
Даже при оптимальных настройках регуляторов качество процессов регулирования тем хуже, чем больше и само запаздывание, и его отношение к постоянной времени объекта 
. Очевидно, на интервале 2τ, пока регулирующее воздействие еще не сказывается на выходе объекта, процесс регулирования совпадает с переходной функцией объекта. При этом динамическая ошибка регулирования не может быть меньше, чем значение выхода апериодического звена при t = 2τ. Если, например, τ = Т, то 
(Т)≈0,63 
, где – установившееся значение выхода объекта (рисунок 50).
Рисунок 51
Графики процессов регулирования при различных значениях отношения τ /Т представлены на рисунке 51: ( а ) - τ =0,2 Т; ( б) - τ = Т;
(1) — переходная функция объекта; (2) — процесс регулирования.
Дата добавления: 2018-05-12; просмотров: 922; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!