Статистические методы изучения взаимосвязей.
1. Метод приведения параллельных данных.
2. Метод аналитических группировок.
3. Графический метод.
4. Балансовый метод.
5. Индексный метод.
6. Корреляционно-регрессионный.
Параметрические методы определения тесноты и направления связи.
Параметрические методы используются в тех случаях, когда все изучаемые признаки являются количественными. Использование этих методов основано на расчете основных параметров распределения (средних показателей, дисперсий).
Дисперсия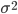 
- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере: 
Дисперсия взвешенная:
правилом сложения дисперсий.
Непараметрические методы определения тесноты связи количественных и качественных признаков.
Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили названиенепараметрических.
Тесноту связи в этом случае оценивают, вычисляя коэффициент ассоциации или коэффициент контингенции.
Для его расчета 4-клеточную корреляционную таблицу:
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
- коэффициент контингенции; 
- коэффициент ассоциации.
; 
.
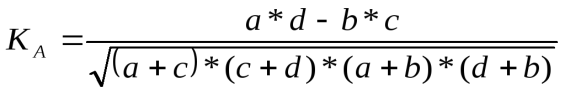Чем ближе коэффициенты по абсолютной величине к 1, тем сильнее связаны м/д собой изучаемые признаки.
|
|
|
Если 
, то это свидетельствует о наличии связи м/д качественными признаками.
Для измерения тесноты зависимости м/д признаками используют ранговые коэффициенты корреляции, когда коррелируют не сами значения показателей, а их ранг, т.е. номера мест, зависимых в каждом ряду значений по возрастанию или убыванию.
Чаще используют коэффициенты корреляции.
- коэффициент корреляции Стермена.
- коэффициент корреляции Кендэлла: 
.
Где n – число наблюдений; 
- разность рангов по переменнымx и y для i – ой единицы совокупности; S – сумма рангов, рассчитываемых по рангам y.
Для любого ранга определяют число рангов данного, из которого вычитают число рангов ниже данного и проводят эту операцию для всех единиц наблюдения.
Коэффициенты изменяются в пределах 
.
Чем ближе абсолютное значение к 1, тем теснее корреляция.
Регрессионный метод анализа связи. Выбор формы уравнения регрессии для анализа экономических явлений. Линейная парная регрессия.
Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения. До регрессионного анализа следует проводить корреляционный анализ, в процессе которого оценивается степень тесноты статистической связи между исследуемыми переменными. От степени тесноты связи зависит прогностическая сила регрессионной модели.
|
|
|
Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.
Уравнение регрессии или модель связи социально-экономических явлений выражается функцией. Различают парную ( 
) и множественную ( 
) регрессии.
Парная регрессий описывает связь между двумя признаками (результативным и факторным). Множественная регрессия описывает связь между результативным признаком и двумя и более факторными признаками.
Представим, что есть два ряда данных:
| x1 | x2 | x3 | … | хn |
| y1 | y2 | y3 | … | yn |
где n – число наблюдений.
Каждое из наблюдений характеризуется двумя переменными xi, yi. Число наблюдений n должно в шесть-семь раз превышать число параметров при переменной х в уравнении регрессии. Таким образом, для изучения линейной регрессии число наблюдений должно быть не менее семи.
|
|
|
В парной линейной регрессии связь между переменными определяется следующим образом:
,
где у – зависимая (объясняемая) переменная, реальная, фактическая, эмпирическая;
х – независимая (объясняющая) переменная;
– зависимая переменная, рассчитанная по уравнению регрессии, теоретическая;
а, b – константы, параметры уравнения линейной регрессии;
– случайная компонента, возмущение.
Каждую пару наблюдений (хi;yi) можно представить в виде точки на плоскости. Такое графическое изображение наблюдений называется полем корреляции или диаграммой рассеяния.
Дата добавления: 2018-05-12; просмотров: 632; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!