Закон сохранения момента импульса.
Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому 
, то есть
или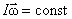 
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы тел, вращающихся вокруг оси z:
отсюда 
или 
.
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы
Собственный момент импульса.
Введем понятие собственного момента импульса системы частиц. Как и момент сил, момент импульса системы зависит, вообще говоря, от выбора точки О, относительно которой его определяют. При переносе этой точки на расстояние 
новые радиус-векторы частиц определяются через старые формулой 
. Поэтому момент импульса системы относительно точки O можно представить так:
или
| (6.20) |
где 
- момент импульса системы относительно точки О', а 
- полный импульс системы.
|
|
|
Из формулы (6.20) следует, что если полный импульс системы 
то ее момент импульса не зависит от выбора точки O. А этим как раз и отличается С-система, в которой система частиц как целое покоится. Отсюда можно сделать третий важный вывод: в С-системе момент импульса системы частиц не зависит от выбора точки, относительно которой его определяют. Этот момент будем называть собственным моментом импульса системы и обозначать 
.
Момент инерции ТТ относительно оси. Теорема Гюгенса - Штейнера.
Моме́нт ине́рции —физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами 
, и моменты инерции тела определяется интегралом
Теорема Гюйгенса — Штейнера
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс 
известен. Необходимо определить момент инерции относительно произвольно оси 
параллельной оси 
. Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
|
|
|
|
Дата добавления: 2018-05-12; просмотров: 325; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!