Центр масс. Уравнение движения СМТ.
Центр тяжести (центр масс) — это точка приложения равнодействующей всех сил тяжести, действующих на каждую из точек системы (абсолютно твердого тела), т.е. точка, в которой как бы сосредоточена масса всей системы (тела).
Координаты (XC, YC) центра тяжести (центра масс) системы материальных точек (рис. 4.1) рассчитывают по формулам
XC=m1x1+m2x2+...+mNxNm1+m2+...+mN;
YC=m1y1+m2y2+...+mNyNm1+m2+...+mN,
где (x1, y1) — координаты материальной точки массой m1; (x2, y2) — координаты материальной точки массой m2 и т.д.
Уравнение движения системы материальных точек
 - импульс системы
- импульс системы 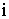 материальных точек.
материальных точек.
 - сила, действующая на систему материальных точек ,
- сила, действующая на систему материальных точек ,
где  - результирующая всех внешних сил.
- результирующая всех внешних сил.
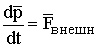 - уравнение движения системы материальных точек.
- уравнение движения системы материальных точек.
Закон изменения импульса системы: скорость изменения импульса системы во времени равно векторной сумме всех внешних сил, действующих на систему.
19. Уравнение движения тела переменной массы. Формула Циолковского.
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива,и т.п.
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты т, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv.
Изменение импульса системы за отрезок времени dt
dp = [(m-dm) (v+dv)+dm (v+u)]-mv,
где и — скорость истечения газов относительно ракеты. Тогда dp=mdv+udm (учли, что dm dv — малый высшего порядка малости по сравнению с остальными).
Если на систему действуют внешние силы, то dp = Fdt, поэтому
Fdt=mdv+udm,
mdv/dt=F-udm/dt. (10.1)
Член -udm/d tназывают реактивной силой
at Fp. Если u противоположен v, то ракета ускоряется, а если совпадает сv, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы ma=F+Fp, которое впервые было выведено И. В.Мещерским.
Применим уравнение (10.1) к движению ракеты, на которую не действуют никакие внешние силы. Полагая F = 0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим
dv dm т dv/dt=-udm/dt. откуда
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса то, то С = uln m0.
Следовательно,
v=uln(m0/m). (10.3)
Это соотношение называется формулой Циолковского. Она показывает, что: 1) чем больше конечная масса ракетыт, тем больше должна быть стартовая масса ракеты то; 2) чем больше скорость истечения и газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Работа силы. Мощность.
Работа силы — это количественная характеристика процесса обмена энергией между взаимодействующими телами.
При прямолинейном движении тела под действием постоянной силы F которая составляет некоторый угол ? с направлением перемещения, работа этой силы равна:
A = Fss = Fs cos
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому этой формулой пользоваться нельзя. Однако на элементарном (бесконечно малом) перемещении drr можно ввести скалярную величину — элементарную работу dA силы F
dA = (F dr )= F cos? ds = Fsds r r Тогда работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути.
Если зависимость Fs от s представлена графически, то работа A определяется площадью заштрихованной фигуры.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности. Мощность N равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
21. Потенциальное поле сил. Потенциальная энергия.
Потенциальная энергия (W) — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Примеры потенциальной энергии:
1) Потенциальная энергия тела массой mна высоте h : W = mgh
2) Потенциальная энергия пружины, растянутой на длину x :
kx2 W =Единица кинетической и потенциальной энергии — Джоуль (Дж).Потенциальное поле — поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Силы, действующие в таких полях, называются консервативными (например, сила тяготения). Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (например, сила трения).
Дата добавления: 2018-05-12; просмотров: 671; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
