Пример решения контрольной работы № 11 (№ 13 для ЗРФ)
По теме: «Статистическая обработка выборки из
Генеральной совокупности значений случайной величины»
Множество однородных объектов, подлежащих статистическому изучению, называется статистической совокупностью. Вся совокупность объектов называется генеральной совокупностью. Ввиду ее большого объема из нее извлекают выборку объема  , хорошо представляющую генеральную совокупность.
, хорошо представляющую генеральную совокупность.
Цель работы - получение выводов о законе распределения генеральной совокупности X и ее характеристиках на основании изучения выборки.
Дан массив чисел  , который является выборкой из генеральной совокупности Х случайных чисел (случайной величины Х).
, который является выборкой из генеральной совокупности Х случайных чисел (случайной величины Х).
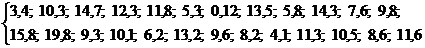 , число значений
, число значений 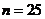 .
.
Задание 1. Построение эмпирической функции распределения и эмпирической плотности распределения случайной величины Х.
1.1 Разбить выборку на частичные интервалы. Найти в заданном массиве чисел  и
и 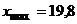 . Для удобства вычисления эти значения целесообразно округлить и взять общий интервал
. Для удобства вычисления эти значения целесообразно округлить и взять общий интервал  , где
, где 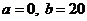 . На этом интервале находятся все случайные числа
. На этом интервале находятся все случайные числа  .Интервал
.Интервал  делим на K равных частичных интервалов. Число K на практике принимают
делим на K равных частичных интервалов. Число K на практике принимают 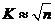 с округлением до целого. Для заданного массива
с округлением до целого. Для заданного массива  . Длина каждого частичного интервала
. Длина каждого частичного интервала  (1.2),
(1.2),  .
.
1.2 Вычислить относительные частоты, плотности относительных частот и накопленные относительные частоты.
Для этого сначала подсчитаем  количество чисел заданного массива, попавших в i-ый интервал
количество чисел заданного массива, попавших в i-ый интервал  .
.
|
|
|
Относительная частота  (аналог вероятности попадания случайной величины Х в i-ый интервал).
(аналог вероятности попадания случайной величины Х в i-ый интервал).  (1.3)
(1.3)
Плотность относительных частот  (аналог теоретической плотности вероятностей)
(аналог теоретической плотности вероятностей)
 (1.4)
(1.4)
Накопленные частоты  (аналог значений теоретической функции распределения вероятностей)
(аналог значений теоретической функции распределения вероятностей)
 , т.е.
, т.е.  (1.5)ит.д.
(1.5)ит.д.
Каждый интервал будет представлять значение его середины 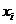 . Представим результаты вычисления в таблице.Таблица 1.
. Представим результаты вычисления в таблице.Таблица 1.
| № интервала | Интервалы | 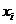
| Подсчет числа значений | 
| 
| 
| 
|
| 1 | 
| 2 | 
| 2 | 0,08 | 0,02 | 0,08 |
| 2 | 
| 6 | 

| 5 | 0,20 | 0,05 | 0,28 |
| 3 | 
| 10 | 

| 11 | 0,44 | 0,11 | 0,72 |
| 4 | 
| 14 | •••• •• | 6 | 0,24 | 0,06 | 0,96 |
| 5 | 
| 18 | • | 1 | 0,04 | 0,01 | 1 |
|
| 
| ||||||
1.3-1.4. а) Гистограмма накопленных относительных частот и график эмпирической функции распределения вероятностей (рисунок 1)
б) Гистограмма плотности относительных частот и график эмпирической функции плотности распределения (плотности вероятностей) (рисунок 2)
|
|
|
По оси ох откладываем интервалы значений случайной величины Х, по оси у – значения  и
и 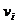 в i-ом интервале(масштабы по оси ох и оу различные). Полученные ступенчатые фигуры, соответственно на рис. 1 и рис. 2, называются гистограммами.
в i-ом интервале(масштабы по оси ох и оу различные). Полученные ступенчатые фигуры, соответственно на рис. 1 и рис. 2, называются гистограммами.









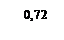




















 а) На рисунке 1: точки, соответствующие
а) На рисунке 1: точки, соответствующие  в правой границе i-ого интервала, соединяем плавной линией. Получим график эмпирической функции распределения вероятностей функции распределения
в правой границе i-ого интервала, соединяем плавной линией. Получим график эмпирической функции распределения вероятностей функции распределения  .
.


Рисунок 2. Гистограмма плотности относительных частот 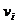 . График эмпирической функции плотности распределения
. График эмпирической функции плотности распределения  (или плотности вероятностей). График теоретической функции плотности вероятностей
(или плотности вероятностей). График теоретической функции плотности вероятностей  .
.

|











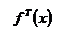








Функция распределения  -неубывающая, изменяется от 0 до 1.
-неубывающая, изменяется от 0 до 1.
Вероятность попадания выборки  в интервал
в интервал  равна разности значений функции распределения
равна разности значений функции распределения  в этих точках.
в этих точках.
|
|
|
Площадь, ограниченная всем графиком функции плотности распределения, равна 1.
По виду графика плотности распределения вероятностей (в виде колокола) можно сделать
предположение, что случайная величина Х распределена по нормальному закону.
Задание 2. Получение статистических оценок параметров распределения случайной величины Х. Вычисление оценок математического ожидания (среднего значения), дисперсии и среднеквадратического отклонения.
1. Оценкой математического ожидания случайной величины Х является выборочное среднее  (2.1)
(2.1)

Математическое ожидание генеральной совокупности  .
.
2. Оценкой дисперсии случайной величины Х является выборочная дисперсия
 или
или 
 (2.2)
(2.2)


Оценка дисперсии  .
.
3. Оценкой среднеквадратического отклонения случайной величины Х является выборочное среднеквадратическое отклонение
 (2.3)
(2.3)
 ,
, 
Задание 3. Построение теоретической кривой плотности вероятностей и теоретической кривой функции распределения.
|
|
|
Мы предположили, что случайная величина Х распределена по нормальному закону, причем математическое ожидание её  , среднеквадратическое отклонение
, среднеквадратическое отклонение  .
.
Функция плотности вероятностей нормального распределения
 (3.1)
(3.1)
Обозначим  (3.2), тогда
(3.2), тогда  (3.3), где
(3.3), где  – функция Гаусса. Для её значений существует таблица
– функция Гаусса. Для её значений существует таблица  (см. приложение таблица I).Причем
(см. приложение таблица I).Причем  . Тогда теоретическая вероятность попадания значения случайной величины в i-ый интервал
. Тогда теоретическая вероятность попадания значения случайной величины в i-ый интервал  (3.4) (аналог формулы 1.4
(3.4) (аналог формулы 1.4 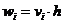 ). Теоретические частоты
). Теоретические частоты  вычисляются по формуле
вычисляются по формуле  (3.5) (аналог формулы 1.3
(3.5) (аналог формулы 1.3  ). Значение теоретической функции распределения найдём по формуле
). Значение теоретической функции распределения найдём по формуле 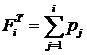 , т.е.
, т.е.  (3.6) (аналог формулы 1.5). По формуле (3.6) найдём значение теоретической функции распределения
(3.6) (аналог формулы 1.5). По формуле (3.6) найдём значение теоретической функции распределения  в конце каждого i-го интервала.
в конце каждого i-го интервала.
Внесем полученные значения в таблицу.
Таблица 2
| № интервала | 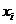
| 
| 
| 
| 
| 
| 
|
| 1 | 2 | -2,05 | 0,049 | 0,013 | 0,052 | 1,3 | 0,052 |
| 2 | 6 | -1,0 | 0,242 | 0,062 | 0,248 | 6,2 | 0,30 |
| 3 | 10 | 0,04 | 0,4 | 0,104 | 0,426 | 10,5 | 0,726 |
| 4 | 14 | 1,08 | 0,22 | 0,057 | 0,228 | 5,7 | 0,954 |
| 5 | 18 | 2,13 | 0,041 | 0,011 | 0,044 | 1,1 | 0,998 |
Нанесем полученные значения  на рисунок 1 (в конце каждого i-ого интервала и соединим полученные точки) и
на рисунок 1 (в конце каждого i-ого интервала и соединим полученные точки) и  на рисунок 2 (в середине каждого i-ого интервала и соединим полученные точки) (используем другие обозначение, _ _ _ _ _).
на рисунок 2 (в середине каждого i-ого интервала и соединим полученные точки) (используем другие обозначение, _ _ _ _ _).
Сравнения эмпирических и теоретических кривых (они близки) визуально подтверждает предположение, что случайная величина Х распределена по нормальному закону.
Задание 4. Проверка гипотезы о нормальном распределении случайной величины Х с помощью критерия Пирсона. Уровень значимости 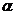 - это допустимая вероятность ошибки отвергнуть верную гипотезу.
- это допустимая вероятность ошибки отвергнуть верную гипотезу.  .
.
Делаем по следующему плану:
1. Выдвигаем гипотезу  : случайная величина Х распределена по нормальному закону с
: случайная величина Х распределена по нормальному закону с 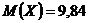 и
и  .
.
2. Альтернативная гипотеза  : случайная величина Х не распределена по нормальному закону.
: случайная величина Х не распределена по нормальному закону.
3. Выбираем критерий проверки гипотезы – критерий Пирсона 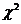 (хи-квадрат)
(хи-квадрат)  .
.
4. Вычисляем фактическое значение критерия Пирсона, при этом  из таблицы 1,
из таблицы 1,  из таблицы 2.
из таблицы 2.

5. По таблице II из приложения находим критическое значение  ,
, 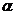 – уровень значимости, это допустимая вероятность ошибки отвергнуть верную гипотезу, у нас
– уровень значимости, это допустимая вероятность ошибки отвергнуть верную гипотезу, у нас  .
.
 . Здесь
. Здесь  – число интервалов,
– число интервалов, 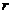 – число параметров, определяющих проверяемый закон; для нормального закона
– число параметров, определяющих проверяемый закон; для нормального закона  (
(  и
и 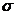 ). Для данного массива
). Для данного массива 
 . По таблице II из приложения находим
. По таблице II из приложения находим  .
.
6. Строим критическую область  , т.е. область значений критерия
, т.е. область значений критерия 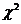 , при котором гипотеза
, при котором гипотеза  отвергается.
отвергается.













Откладываем фактическое значение  . Так как значение
. Так как значение  не попало в критическую область, то принимаем гипотезу
не попало в критическую область, то принимаем гипотезу  .
.
Задание 5. Вывод.
Была проведена статистическая обработка массива чисел  , который является выборкой из генеральной совокупности Х.
, который является выборкой из генеральной совокупности Х.
5.1 Были построены графики эмпирической функции распределения  и эмпирической функции плотности
и эмпирической функции плотности  вероятностей.
вероятностей.
5.2 По виду графика эмпирической функции плотности вероятностей было сделано предположение о нормальном законе распределения генеральной совокупности Х.
5.3 Были определены выборочные среднее значение  и среднеквадратическое отклонение
и среднеквадратическое отклонение 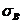 .
.
5.4 Исходя из предположения, что генеральная совокупность Х распределена по нормальному закону с параметрами 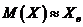 и
и  , были вычислены теоретические значения функции плотности вероятностей и функции распределения и построены графики
, были вычислены теоретические значения функции плотности вероятностей и функции распределения и построены графики  и
и  . Была отмечена близость теоретических и эмпирических графиков.
. Была отмечена близость теоретических и эмпирических графиков.
5.5 С помощью критерия Пирсона была проверена гипотеза  о том, что генеральная совокупность Х распределена по нормальному закону. Гипотеза
о том, что генеральная совокупность Х распределена по нормальному закону. Гипотеза  подтвердилась.
подтвердилась.
Итак, генеральная совокупность Х, представленная выборкой, распределена по нормальному закону с математическим ожиданием  и среднеквадратическим отклонением
и среднеквадратическим отклонением 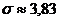 .
.
Дата добавления: 2018-05-09; просмотров: 240; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

