Контрольной работы № 12 для ЗРФ
Пример к заданию № 1:
а) Представить функцию 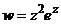 , где
, где 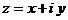 в виде
в виде 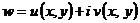 ;
;
б) Проверить, является ли она аналитической;
в) Если 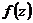 – аналитическая, то найти производную в точке
– аналитическая, то найти производную в точке 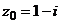 .
.
а) 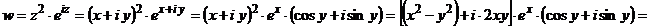
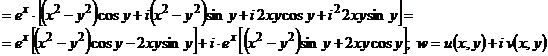
Следовательно, 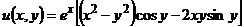 ;
; 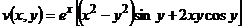 .
.
б) Проверяем аналитичность по формулам Коши-Римана (по 4.3) 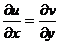 и
и 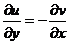 . Напомним, что беря частную производную по одной переменной, считаем другую переменную – постоянной.
. Напомним, что беря частную производную по одной переменной, считаем другую переменную – постоянной.

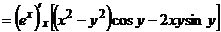
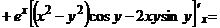
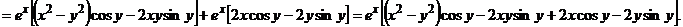
(х – постоянная, тогда 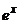 - тоже постоянная)
- тоже постоянная)
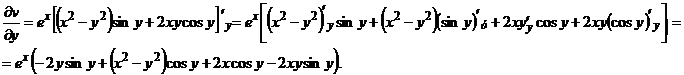
Очевидно, 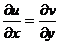 .
.
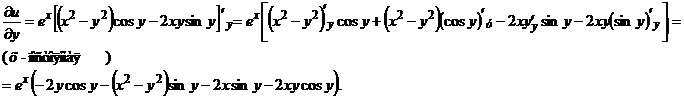
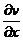
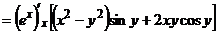
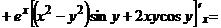
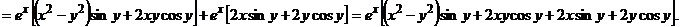
(у – постоянная).
Как видно 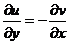 . Следовательно, функция аналитическая всей комплексной плоскости z.
. Следовательно, функция аналитическая всей комплексной плоскости z.
в) Находим производную в точке 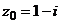 .
. 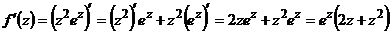 .
.
Пусть 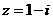 , тогда
, тогда 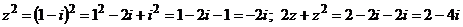 .
.
По (3.3) 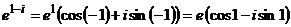 ;
; 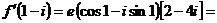
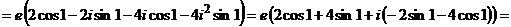
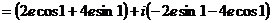 .
.
К заданию № 2 дадим 3 примера:
Пример 1 к заданию № 2:
Разложить функцию 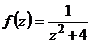 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки 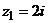 .
.
Надо получить разложение по степеням 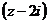 .
.
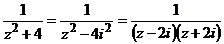 . По правилу 5.2.5.
. По правилу 5.2.5. 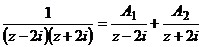 ;
;
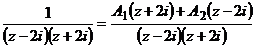 ;
; 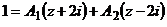 или
или 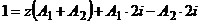 ;
;
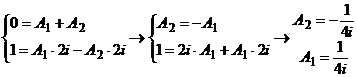 ;
; 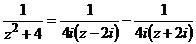 .
.
Разложим в ряд функцию 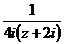 по 5.2.2
по 5.2.2
1) Внутри круга с центром в точке 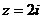 радиуса
радиуса 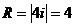 .
.
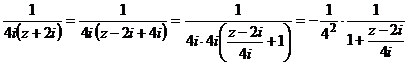 при
при 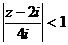 можно воспользоваться формулой (6) рядов Маклорена для
можно воспользоваться формулой (6) рядов Маклорена для 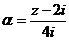 .
. 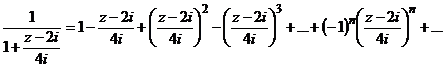
Тогда 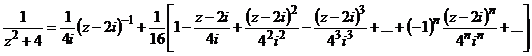 при
при 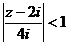 .
.
2) Вне круга с центром в точке 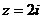 радиуса
радиуса 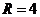 .
.
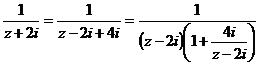 при
при 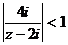 по формуле (6) для рядов Маклорена для
по формуле (6) для рядов Маклорена для 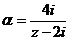 .
.
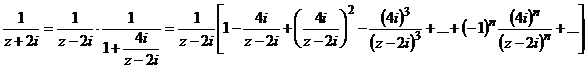 и
и
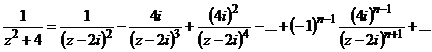 , при
, при 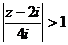 .
.
Пример 2 к заданию № 2:
Разложить функцию 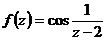 в окрестности точки
в окрестности точки 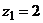 . Воспользуемся формулой (3) таблицы рядов Маклорена для
. Воспользуемся формулой (3) таблицы рядов Маклорена для 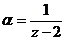 .
.
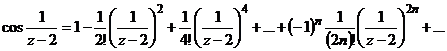
Пример 3 к заданию № 2:
Разложить функцию 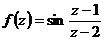 в окрестности точки
в окрестности точки 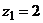 .
.
Преобразуем 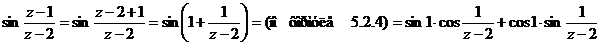 .
.
Воспользуемся формулами (2) и (3) таблицы рядов Маклорена для 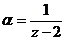 .
.
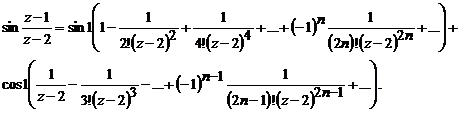
Приложения к контрольной работе № 12
I Таблица основных производных
|
|
|
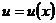 ,
, 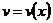 – функции от х , с, а, const – постоянные числа,
– функции от х , с, а, const – постоянные числа, 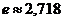
1–1)  ; 1–2)
; 1–2) 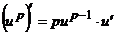 ; 1–3)
; 1–3) 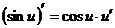 ; 1–4)
; 1–4) 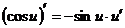 ;
;
1–5) 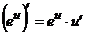 .
.
Основные правила дифференцирования
2–1) 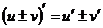 ; 2–2)
; 2–2) 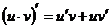 ; 2–3)
; 2–3) 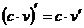 (с – число); 2–4)
(с – число); 2–4) 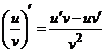
II Таблица рядов Маклорена 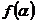 в окрестности
в окрестности 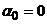 ,
, 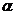 – функция от z,
– функция от z, 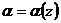
| № | Ряд | Интервал сходимости |
| 1 | 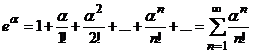
| 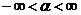
|
| 2 | 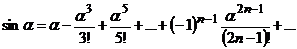
| 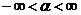
|
| 3 | 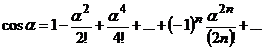
| 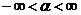
|
| 4 | 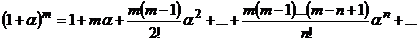
| 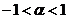
|
| 5 | 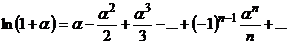
| 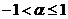
|
| 6 | 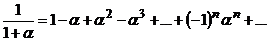
| 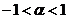
|
| 7 | 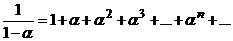
| 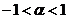
|
| 8 | 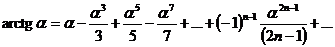
| 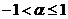
|
| 9 | 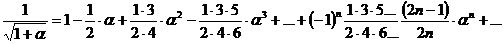
| 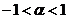
|
Варианты заданий контрольной работы № 12 для ЗРФ
Тема: «Элементы теории функций комплексного переменного»
Задание 1:
а) Представить заданную функцию 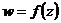 , где
, где 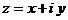 в виде
в виде 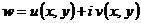 ;
;
б) Проверить является ли 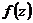 аналитической;
аналитической;
в) Если 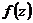 – аналитическая, то найти значение её производной в точке
– аналитическая, то найти значение её производной в точке 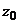 .
.
Задание 2: Разложить функцию 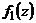 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки 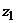 .
.
| № вар-та | 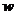
| 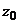
| 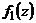
| 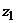
|
| 1 | 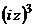
| 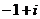
| 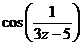
| 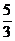
|
| 2 | 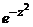
| 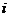
| 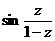
| 1 |
| 3 | 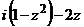
| 1 | 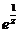
| 0 |
| 4 | 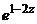
| 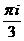
| 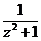
| 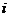
|
| 5 | 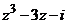
| 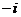
| 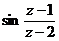
| 2 |
| 6 | 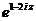
| 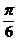
| 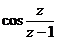
| 1 |
| 7 | 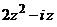
| 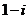
| 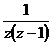
| 0 |
| 8 | 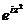
| 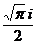
| 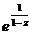
| 1 |
| 9 | 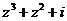
| 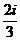
| 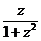
| 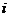
|
| 10 | 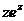
| 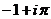
| 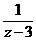
| 1 |
Контрольная работа № 13 (I)
Тема: «Теория вероятностей»
Краткая теория и методические указания.
1. Случайные события
Вероятность события А – это число, характеризующее возможность наступления этого события при некоторых испытаниях (опытах).
Классическое определение вероятности. Вероятность события 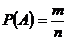 , где m – число благоприятных для этого события исходов опыта, n – общее число всех элементарных исходов
, где m – число благоприятных для этого события исходов опыта, n – общее число всех элементарных исходов 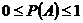 .
.
|
|
|
События А и В называются несовместными, если в результате опыта появление одного события исключает появление другого.
События А и В называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого.
Суммойсобытий А + В называется событие С, состоящее в появлении хотя бы одного из событий А и В (или А или В или обоих вместе).
Произведением (пересечением) событий 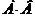 называется событие D, которое состоит в том, что произошли одновременно оба события А и В (и А и В).
называется событие D, которое состоит в том, что произошли одновременно оба события А и В (и А и В).
Событие 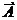 называется противоположным событию А, если в результате опыта может произойти только одно из событий А или
называется противоположным событию А, если в результате опыта может произойти только одно из событий А или 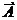 .
. 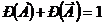 .
.
Вероятность суммы событий А и В 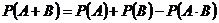 .
.
Для несовместных событий А и В : 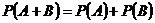 .
.
1.10 Теорема умножения вероятностей независимых событий 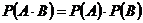 .
.
1.11 Условной вероятностью 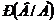 называется вероятность события В, вычисленная в предположении, что событие А уже наступило.
называется вероятность события В, вычисленная в предположении, что событие А уже наступило.
1.12 Теорема умножения вероятностей зависимых событий 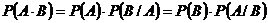 .
.
1.13 Формула полной вероятности. Пусть событие А может произойти с одной из гипотез 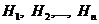 . События
. События 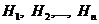 – несовместные и
– несовместные и 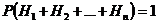 . Тогда
. Тогда 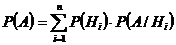 .
.
|
|
|
1.14 Формула Байеса или апостериорные вероятности гипотез.
Пусть событие А, которое могло произойти с одной из гипотез 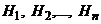 , произошло в результате опыта. Априорные (до опыта) вероятности гипотез были равны
, произошло в результате опыта. Априорные (до опыта) вероятности гипотез были равны 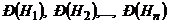 . Апостериорные (после опыта) вероятности гипотез
. Апостериорные (после опыта) вероятности гипотез 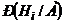 при том, что событие А произошло, вычисляются по формулам
при том, что событие А произошло, вычисляются по формулам 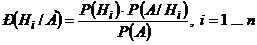 , где
, где 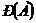 – вероятность события А вычисляется по формуле полной вероятности 1.13
– вероятность события А вычисляется по формуле полной вероятности 1.13 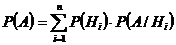 . Апостериорные вероятности гипотез
. Апостериорные вероятности гипотез 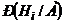 не равны априорным вероятностям
не равны априорным вероятностям 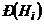 .
.
2. Случайные величины (СВ)
Случайной величиной Х называется величина, которая случайно принимает какое-то значение из совокупности своих значений.
Функция распределения 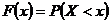 . Функция распределения – неубывающая, непрерывная слева функция, определённая на всей числовой оси, при этом
. Функция распределения – неубывающая, непрерывная слева функция, определённая на всей числовой оси, при этом 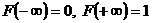 .
.
2.2.1 Вероятность того, что случайная величина Х примет значение в интервале 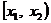 равна
равна 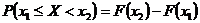 .
.
Дискретные случайные величины (ДСВ). Значениями их являются только отдельные точки числовой оси.
2.3.1 Закон распределения ДСВ Х можно задать в виде ряда распределений
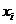
| 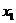
| 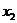
| 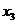
| … | 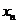
|
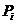
| 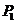
| 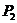
| 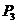
| … | 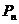
|
В первой строке таблицы указаны все значения х ДСВ Х, а во второй строке – вероятности 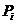 принятия значения
принятия значения 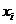 .
. 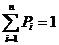 .
.
2.3.2 Функция распределения ДСВ Х выражается формулой 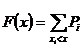 .
. 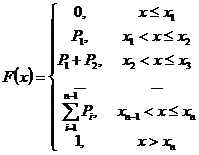 .
.
|
|
|
График 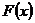 представляет собой ступенчатую линию.
представляет собой ступенчатую линию.
Непрерывные случайные величины (НСВ). НСВ принимает свои значения непрерывно на некотором интервале числовой оси.
2.4.1 Закон распределения НСВ задаётся функцией плотности распределения 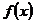 ,
, 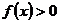 .
.
2.4.2 Функция распределения НСВ вычисляется по формуле 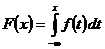 . График
. График 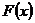 НСВ представляет собой непрерывную неубывающую кривую.
НСВ представляет собой непрерывную неубывающую кривую. 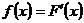 .
.
2.4.3 Площадь под графиком 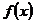 равна 1, так как
равна 1, так как 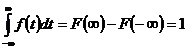 .
.
2.4.4 Вероятность того, что НСВ Х примет значения в интервале 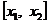 равна
равна 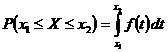 . При
. При 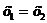
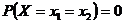 . Вероятность отдельного значения равна нулю.
. Вероятность отдельного значения равна нулю.
3. Числовые характеристики случайных величин
Математическое ожидание 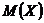 – это среднее значение совокупности значений СВ.
– это среднее значение совокупности значений СВ.
Для ДСВ 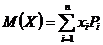 , для НСВ
, для НСВ 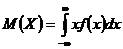
Дисперсия 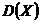 характеризует степень разброса значений СВ от своего среднего значения
характеризует степень разброса значений СВ от своего среднего значения 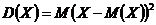 . Пусть
. Пусть 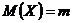 .
.
Для ДСВ: 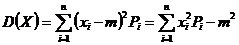 , для НСВ:
, для НСВ: 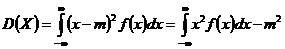 .
.
Среднее квадратическое отклонение 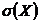 .
. 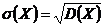 – это абсолютное отклонение СВ от своего среднего значения.
– это абсолютное отклонение СВ от своего среднего значения.
4. Нормальное распределение
Оно самое распространенное распределение в природе, экономике и т.д. Обозначается 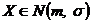 , где
, где 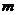 и
и 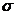 – параметры нормального распределения,
– параметры нормального распределения, 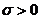 .
.
Функция плотности вероятностей 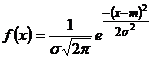 .
. 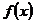 определена на всей числовой оси,
определена на всей числовой оси, 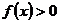 ;
; 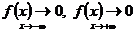 . Функция
. Функция 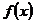 достигает при
достигает при 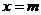 максимума, равного
максимума, равного 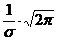 и имеет точки перегиба в точках
и имеет точки перегиба в точках 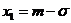 и
и 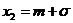 . При изменении значения
. При изменении значения 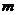 график
график 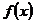 целиком перемещается вдоль оси х. При изменении значения
целиком перемещается вдоль оси х. При изменении значения 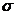 график
график 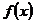 изменяется так: при увеличении значения
изменяется так: при увеличении значения 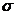 в k раз максимальное значение
в k раз максимальное значение 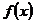 уменьшается в k раз и график выполаживается.
уменьшается в k раз и график выполаживается.
Математическое ожидание 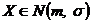
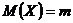 , дисперсия
, дисперсия 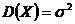 .
.
Функция распределения 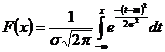 .
.
Нормированное нормальное распределение 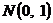 .
. 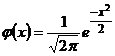 – функция Гаусса,
– функция Гаусса,
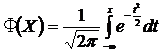 – функция Лапласа.
– функция Лапласа. 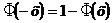 . Составлены таблицы этих функций. Они используются для вычисления задач для
. Составлены таблицы этих функций. Они используются для вычисления задач для 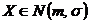 . При этом
. При этом 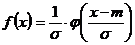 ,
, 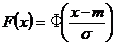 .
.
Вероятность того, что 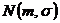 примет значения в интервале
примет значения в интервале 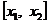
 .
.
Дата добавления: 2018-05-09; просмотров: 347; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
