Контрольной работы №11 для ЗРФ
Тема: Уравнения математической физики.
Задание: Найти решение уравнения теплопроводности на отрезке  ,
, 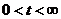 ;
;  ,
,  удовлетворяет:
удовлетворяет:
а) начальным условиям  ;
;
б) граничным условиям 
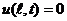 .
.
| № вар-та | 
| 
| 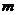
| 
| 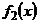
|
| 1 | 16 | 3 | 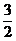
| 
| 
|
| 2 | 1 | 2 | 1 | 
| 
|
| 3 | 25 | 5 | 
| 
| 
|
| 4 | 16 | 4 | 2 | 
| 
|
| 5 | 4 | 5 | 
| 
| 
|
| 6 | 1 | 3 | 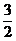
| 
| 
|
| 7 | 25 | 8 | 4 | 
| 
|
| 8 | 9 | 2 | 1 | 
| 
|
| 9 | 16 | 1 | 
| 
| 
|
| 10 | 4 | 4 | 2 | 
| 
|
Контрольная работа № 12 для ЗРФ
Тема: «Элементы теории функций комплексного переменного»
Краткие теоретические сведения.
1. Комплексное число 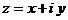 . i – мнимая единица,
. i – мнимая единица,  , т.е.
, т.е.  . х, у – любые действительные числа; х – действительная часть, а у – мнимая часть комплексного числа.
. х, у – любые действительные числа; х – действительная часть, а у – мнимая часть комплексного числа.
Запись:  .
.
1.1. Комплексное число 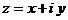 представляется точкой
представляется точкой  плоскости хоу (комплексной плоскости z).
плоскости хоу (комплексной плоскости z).
1.2. Тригонометрическая форма комплексного числа  , где
, где 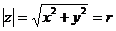 – модуль,
– модуль,  .
.  – аргумент комплексного числа z.
– аргумент комплексного числа z.  .
.  .
.
1.3. Показательная форма комплексного числа  .
.
1.4.  и т.д.
и т.д.  .
.
1.5. Пусть  .
.
1.5.1  .
.
1.5.2  .
.
1.5.3  .
.
1.5.4  .
.
2. Функция комплексного переменного.
Пусть 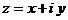 , функция
, функция 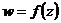 может быть представлена в виде двух действительных функций u и v от действительных переменных х и у.
может быть представлена в виде двух действительных функций u и v от действительных переменных х и у.  ,
,  .
.
Примеры: 1)  , тогда
, тогда  ;
;
2) 

 .
.
3. Элементарные функции комплексного переменного.
3.1. Степенная функция  , n – целое, положительное число.
, n – целое, положительное число.
Пусть 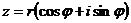 , тогда
, тогда 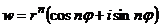 .
.
3.2.  – корень целой положительной степени, если
– корень целой положительной степени, если 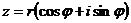 , то
, то  – n-значная функция при
– n-значная функция при  .
.
|
|
|
3.3. Показательная функция.
Пусть 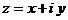 ,
,  .
.
3.4. Логарифмическая функция.

 .
. 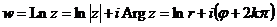 – бесконечнозначная функция.
– бесконечнозначная функция.
3.5. Тригонометрические функции.
Пусть 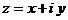 .
.  .
.
4. Производная функция комплексного переменного.
4.1. Пусть 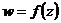 определена и однозначна в некоторой окрестности точки
определена и однозначна в некоторой окрестности точки 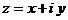 .
.
 , где
, где  – приращения.
– приращения.
4.2. Если 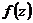 имеет производную во всех точках области D, то
имеет производную во всех точках области D, то 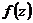 называется аналитической в области D. Точки плоскости z, в которых
называется аналитической в области D. Точки плоскости z, в которых 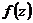 не определена или не является аналитической, называются особыми.
не определена или не является аналитической, называются особыми.
4.3. Необходимые и достаточные условия аналитичности функции 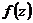 (условие Коши-Римана или Эйлера-Даламбера). Однозначная функция
(условие Коши-Римана или Эйлера-Даламбера). Однозначная функция  , где
, где 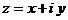 аналитична в точке z и её окрестностях, тогда и только тогда, когда
аналитична в точке z и её окрестностях, тогда и только тогда, когда 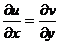 и
и 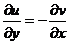 .
.
4.4. Для нахождения производной  применяются обычные правила дифференцирования.
применяются обычные правила дифференцирования.
5. Ряд Лорана для функции 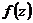 с центром в точке
с центром в точке  имеет вид.
имеет вид.
5.1. 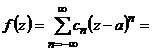
или 
5.2. Приёмы разложения функции в ряд Лорана в окрестности точки  .
.
5.2.1. Используют разложение в ряд Маклорена основных элементарных функций, беря 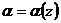
5.2.2. Если надо получить разложение функции  в окрестности
в окрестности 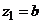 , то надо представить функцию
, то надо представить функцию 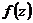 в двух областях аналитичности:
в двух областях аналитичности:
1) внутри круга с центром в точке b, радиуса  .
.
|
|
|
 , можно воспользоваться табличным рядом Маклорена (6) для
, можно воспользоваться табличным рядом Маклорена (6) для  при
при  .
.
2) вне круга с центром в точке b, радиуса  .
.
 , можно воспользоваться табличным рядом Маклорена (6) для
, можно воспользоваться табличным рядом Маклорена (6) для  при
при  , т.е.
, т.е. 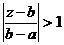 .
.
5.2.3. Разложения для  можно получить продифференцировав ряд для
можно получить продифференцировав ряд для  , т.к.
, т.к. 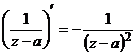 .
.
5.2.4. Часто надо предварительно преобразовать разлагаемую в ряд функцию, применив формулы:  ;
;  ;
;  . Например, если надо разложить
. Например, если надо разложить  в окрестности
в окрестности  .
.

5.2.5. Рациональную дробь надо представить в виде суммы простейших дробей
 . А1 и А2 получим, приведя правую часть тождества к общему знаменателю и приравняв числители дробей слева и справа.
. А1 и А2 получим, приведя правую часть тождества к общему знаменателю и приравняв числители дробей слева и справа.
 . Получим систему уравнений относительно А1 и А2
. Получим систему уравнений относительно А1 и А2  .
.
Примеры выполнения заданий
Дата добавления: 2018-05-09; просмотров: 225; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
