Затраты энергии на ведение процесса измельчения. Шаровая мельница. Расчет частоты вращения барабана.
Эта формула была рекомендована для определения расхода энергии, затрачиваемой на измельчение материала:
Барабанно-шаровая мельница — устройство для измельчения твёрдых материалов. Применяется в основном горнорудной промышленности, для создания порошка для использования в красках, пиротехнических средствах, и в керамике.
Расчет критической 
и рабочей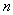 
частоты вращения барабана. Величина определяется из условия отрыва шара от поверхности барабана: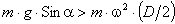 
. Учитывая, что 
и в верхней точке подъема (т.А) 
, получим: 
. Рабочую частоту вращения барабана 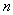рекомендуют принимать равной (0.75-0.8)* .
Тепловые процессы, классификация, движущая сила, основное кинетическое уравнение. Способы интенсификации процессов
Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. К тепловым процессам относят процессы, связанные с переносом энергии в виде тепла от более нагретого тела к менее нагретому. Энергия переносится от более высокого энергетического потенциала к более низкому. Движущей силой тепловых процессов явл. разность температур. Тепловые процессы делят на 4 группы: 1) процесс нагрева; 2)процесс конденсации; 3)выпаривание; 4)охлаждение. ∆Н=с1t1-c2t2; ∆t=t1-t2.
Эти процессы описываются общим кинетическим уравнением.
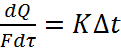, где Q - количество передаваемого тепла, Дж
– удельный тепловой поток, Вт/м2; К – коэффициент теплопередачи;
|
|
|
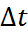- разность температур.
В процессе теплообмена тепло может переноситься следующими основными способами: теплопроводностью, конвекцией, тепловым излучением. Цель интенсификации тепловых процессов заключается в повышении эффективности работы аппаратов и снижении расхода ими тепловой энергии. В качестве самых важных направлений интенсификации можно выделить следующие: интенсификация теплообменных процессов, утилизация теплоты, т.е. ее регенерация. Эффективность теплообмена обусловлена величиной коэффициентов теплоотдачи и термического сопротивления стен.
Перенос тепла за счет теплопроводности. Закон Фурье. Дифференциальное уравнение теплопроводности и решение его для случая плоской стенки
Основным законом передачи тепла теплопроводностью является закон Фурье, согласно которому количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный тепловому потоку, за время dτ прямо пропорционально температурному градиенту ∂t/∂n, поверхности dF и времени dτ: dQ= -λ·∂t/∂n·dF·dτ, или количество тепла, передаваемое через единицу поверхности в единицу времени q=Q/Fτ= -λ ∂t/∂n. Величина q называется плотностью теплового потока. Знак минус, стоящий перед правой частью уравнений, указывает на то, что тепло перемещается в сторону падения температуры. Коэффициент пропорциональности λ называется коэффициентом теплопроводности, Вт/м·град, его значение зависит от физических св-в среды.
|
|
|
Дифференциальное ур-е теплопроводности (ур-е Фурье) определяет температуру в любой точке тела, через которое тепло передается теплопроводностью и записывается в виде:
, где а=λ/сρ – коэффициент температуропроводности, м2/сек
- оператор Лапласа.
Уравнение теплопроводности для плоской стенки при установившемся процессе теплообмена: Q = λ/δ(tст1-tст2)F, λ-коэф. теплопроводности материала стенки; δ-толщина стенки; tст1-tст2 – разность температур поверхности стенки; F- поверхность стенки.
Дата добавления: 2018-05-02; просмотров: 630; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!