Назначение, способы ведения процесса фильтрования. Движущая сила процесса фильтрования и способы ее создания.
Проц-м фильтрования наз. проц. разделения жидких и газовых неоднородных сист. с помощью пористых перегородок, которые наз. фильтр-ые перегородки. В последнее время проц-ы фильтр-я дополнены специф-ми проц-ми, кот-е находят применение в пищ. пром-ти (ультрафильтрация, обратный осмос). Т.о. проц-ы фильтр-я составляют сами проц-ы фильтр-я, проц-ы ультраф-и и обратного осмоса. Движущей силой этих проц-в явл. разность давлений до и после фильтров перегор.
В зависимости от способов создания и поддержания движ. силы проц-ы фильтр-я протекают с:
1) Постоянной скор-ю проц.
2) падающей скор-ю проц.
Объяснение этому заключ-ся в кинетич. уравнении проц. фильтр-я
В левой части V- получаемого фильтрата, F- площадь фильтр-ой перегородки ; 
- длительность проц.
– скорость проц фильтр-я ( 
)
Скорость пропорциональна R- сопротивлению протекания пр-са, 
p- движущая сила.
Если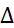 
p – const, 
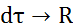, то ↓. Если 
Различают пр-с фил-я по способу задержания распределит-й фазы, на фильтр-е с образов. осадка и фильтр-е с постеп-ым закупор-ем пор.
| Первый случай пр-са фил-я осуществляется тогда, когда размер пор в фильтр-ой перегородке меньше диаметра частиц (dп<dч) | Второй случай: частицы задерживаются внутри пор(dч<dп). Перегородка назыв. глубинной. |
| 
|
Раздел-е неоднор. систем характериз-ся полидисперсностью частиц, т.е. в распределяемой фазе наход. частицы разл-х размеров. Эти частицы задержив-ся как на поверхн-ти, так и внутри в порах. Тогда фильтр-я перегородка назыв. поверхностно-глубинной.
|
|
|
С точки зрения эксплуатации аппарата желат-но чтобы перегородки работали с образов-ем осадка на поверхн-ти. В этом случае появл. возможность восстановить фильтр-ю поверхн-ть после снятия осадка с неё. Глубинные перегородки регенерации не подверг-ся.
Создание движущей силы пр-са фильтрования
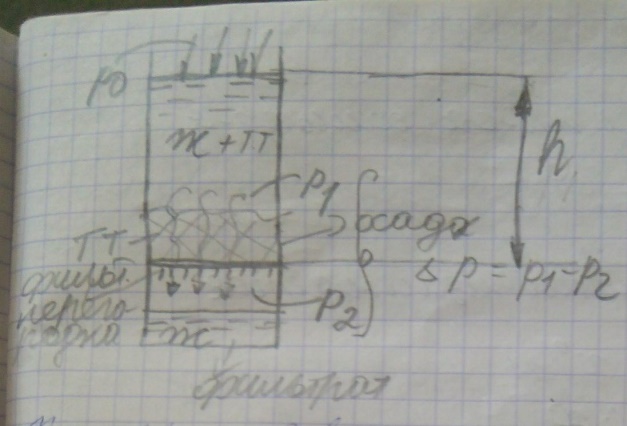
| Пусть давление под перегородкой p2 = рaтм
p1 = ратм+ 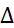р = ризб
Способы создания давления
1)  =  +  gh – осн уравнение гидрос-ки
–давл-е на свободный пов-ти
gh - давление гидростатич. столба жидкости.
|
= gh, h – высота столба жидкости.
2) 
, = 
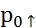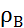*g*НВ
3) НВ – напор, создав-й вентилятором
4) В пром-ти жидкую неоднор. систему подают с помощью насоса
= 
*g*НН
Hн – напор развиваемый насосом
- суспензии
Если 
< ратм – вакуумное фильтр-е, при нём для увеличения движущей силы (над перегородкой) может создав-ся любым ранее рассмотренным способом. Максим-я глубина = - 1 атм.
Закон Дарси. Вывод основного уравнения процесса фильтрования и его решение для случая фильтрования с образованием осадка.
Закон Дарси — закон фильтрации жидкостей и газов в пористой среде.
|
|
|
Определяет расход однородной жидкости через пористую среду при ламинарном ре- жиме потока следующей формулой:
Q = (k * F * (P1 - P2))/μ * L
где:- Q - расход жидкости, м3/с, k - коэффициент проницаемости, м2, F - площадь фильтрации пористой среды, м2, (P1 - Р2) -разность давлений, созданных на концах испытуемого образца, Па, L - длина испытуемого образца породы, м, µ -абсолютная вязкость жидкости, мПа·с.
На основании закона Дарси определяют коэффициент проницаемости k - существенную величину дляхарактеристики физических свойств нефтеносных пород.
Единицей проницаемости в СИ является квадратный метр. В практических приложениях в качестве единицы часто используется дарси (1 Д ≈ 10-12 м²).
Основной характеристикой процесса является скорость фильтрования - объем фильтрата, получаемый за единицу времени с единицы поверхности фильтра.
Согласно закону Дарси, основное кинетическое уравнение фильтрования имеет вид:
,
где 
– перепад давления на фильтровальном слое (движущая сила процесса), Па;
– коэффициент динамической вязкости фильтрата, Па·с;
– гидравлическое сопростивление потоку фильтрата (сопротивление фильтровального слоя), м-1.
Сопротивление фильтровального слоя 
складывается из сопротивлений фильтровальной перегородки и слоя осадка на ней.
|
|
|
. (4.31)
Поэтому
, (4.32)
где, 
и 
– гидравлическое сопротивление слоя осадка и фильтровальной перегородки, м-1.
Величину в процессе фильтрования в первом приближении можно принимать постоянной, пренебрегая некоторым возможным ее увеличением вследствие проникания в поры перегородки твердых частиц. Сопротивление слоя осадка с увеличением его количества изменяется от нуля в начале фильтрования до максимального значения в конце процесса.
Если осадок несжимаемый, то
, (4.33)
где 
– высота слоя осадка, м;
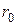– удельное объемное сопротивление осадка, м-2. Это сопротивление, оказываемое потоку фильтрата равномерным слоем осадка высотой 1 м.
Выразим высоту осадка через его объем 
и площадь 
:
. (4.34)
С течением времени высота слоя осадка увеличивается, т.е. объем полученного осадка пропорционален объему фильтрата 
:
, откуда объемная доля осадка по отношению к фильтрату 
равна:
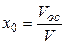. (4.35)
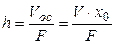. (4.36)
Подставим выражения (4.36), (4.33), (4.29) в (4.32) получим:
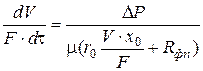, (4.37)
Уравнение (4.37) – основное дифференциальное уравнение фильтрования с образованием несжимаемого осадка на несжимаемой перегородке. Величины ,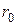 
и в уравнении (4.37) постоянны и не зависят от . Уравнение (4.37) применимо только к ламинарному течению жидкости в порах осадка. Это допущение основано на том, что при малых размерах пор и скоростях течения числа Рейнольдса невелики.
|
|
|
При интегрировании уравнения (4.37) необходимо принимать во внимание условия (режим) процесса фильтрования.
Дата добавления: 2018-05-02; просмотров: 1424; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!