Уравнения материальных балансов и механизм разделения неоднородных систем в поле действия сил тяжести. Свободное и стесненное отстаивание. Режимы отстаивания
Материальный баланс процесса отстаивания:
Пусть разделению подлежит система, сост. из вещества а (сплошной фазы) и взвешенных частиц веществ b (дисперсной фазы). Введем обозначения:
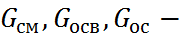 масса исходной смеси, осветленной жидкости и получаемого осадка, кг;
масса исходной смеси, осветленной жидкости и получаемого осадка, кг;
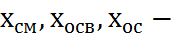 содержание вещества b в исходной смеси, осветленной жидкости и осадке, массовые доли.
содержание вещества b в исходной смеси, осветленной жидкости и осадке, массовые доли.
При отсутствии потерь вещества в процессе разделения уравнения материального баланса имеют вид:
По общему количеству веществ
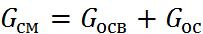
По дисперсной фазе (веществу b):
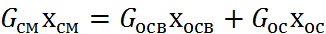
Совмесное решение уравнений позволяет определить массу осветленной жидкости и массу осадка, получаемых при заданном содержании вещества b в осадке и осветленной жидкости:
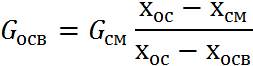
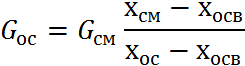
Содержание взвешенных частиц в осветленной жидкости и в осадке выбирается в зависимости от конкретных технологических условий процесса разделения. При этом содержание вещества в осветленной жидкости обычно ограничивается некоторым нижним пределом.
Осаждение частиц под действием сил тяжести. Если частица массой m начинает падать под действием силы собственного веса, то скорость ее движения первоначально возрастает со временем. При полном отсутствии сопротивления среды скорость w менялась бы во времени по известному закону w=g 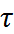 . Однако с увеличением скорости будет расти сопротивление движению частицы и соответственно уменьшится ее ускорение. В результате через короткий промежуток времени наступит равновесие: сила тяжести, под действием которой частица движется, станет равна силе сопротивления среды. Начиная с этого момента, ускорение движения будет равно нулю и частица станет двигаться равномерно – с постоянной скоростью. Скорость такого равномерного движения частицы в среде называют скоростью осаждения и обозначают
. Однако с увеличением скорости будет расти сопротивление движению частицы и соответственно уменьшится ее ускорение. В результате через короткий промежуток времени наступит равновесие: сила тяжести, под действием которой частица движется, станет равна силе сопротивления среды. Начиная с этого момента, ускорение движения будет равно нулю и частица станет двигаться равномерно – с постоянной скоростью. Скорость такого равномерного движения частицы в среде называют скоростью осаждения и обозначают 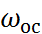 .
.
Скорость осаждения можно найти из условия равенсва силы, движущей частицу, и силы сопротивления среды:
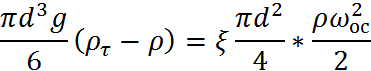
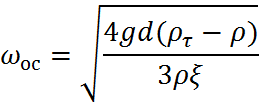
При значительной концентрации твердых частиц в среде происходит стесненное осаждение, скорость которого меньше, чем свободного, в следствии трения и соударения между частицами.
Расчёт скорости процесса отстаивания. Уравнение Стокса.
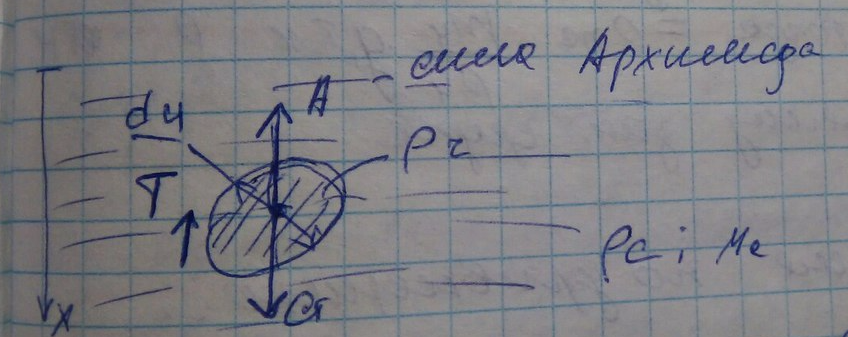
Fβ=G-A-T – внешняя сила (G-сила тяжести, A-сила Архимед, T-сила трения(частица движется)). G,A,T-движущие силы системы.
При ее определении рассмотрим частицу,кот. находится в сплошной среде с ρс и μс-вязкость среды. Отстаивание идёт свободное, влияние др. частиц отсутствует. Частица обладает ρч, частица имеет форму сферы и dч-диаметр.
Выделение происходит под действием силы тяжести. Возникают силы сопротивления T жидкости.
Применим принцип динамики: перемещение частицы вызвано действием внешней силы, величина которой равна равнодействующей от всех сил, действующих на частицу.
Внешняя сила Fβ будет установл. на основе 2-го з-на Ньютона: всякая сила = есть произведение массы Fβ = mч*dv/dτ.
Сила тяжести: G=mчg (из 3-го закона Ньютона)
Архимедова или выталкивающая сила = весу жидкости вытесненную телом:
Gж= A=mж*g=ρж*Vж*g= ρж*mч/ ρч*g т.к. ρ- отношение массы к объёму среды
Vж=Vч, тогда
Сила трения может быть определена через давление по ур-ю Дарси: Т= f*▲р= ξfρ 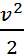
f – площадь сечения частицы; ξ- коэф. сопротивления частиц
Подставляем знак физической величины
mч 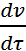 = mч*g- ρж* mч/ ρч*g-ξfρ*
= mч*g- ρж* mч/ ρч*g-ξfρ* 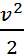
Делим на mч и получаем;
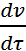 =g-
=g- 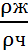 *g-ξf
*g-ξf 
При выделении жидких частиц из среды
0=g*(1- ρж / ρч) - ξf 
ξf 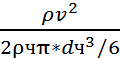 = g(ρч-ρс/ ρч)
= g(ρч-ρс/ ρч)
Определим скорость процесса отстаивания
v2=(4/3*g*dч*( ρч-ρс))/ ξ* ρс - зависимость определения скорости отстаивания ( для разных режимов)
Скорость отстаивания для ламинарного режима
v = g*(dч2*( ρч-ρс))/18μс
Из получ.выражения: v пр-а отстаивания пропорционально размеру выделенной частицы, движущей силе пр-са и обратно пропорционально вязкости системы.
Из анализа этой зависимости – методы интенсификации:
Для увеличения скорости процесса необходимо:
- увеличить размер выделяемой частицы (коагуляцию частиц): газ-электр.коагулят.
- увеличить движущую силу процесса – в жидк. неоднородн. сист. при увелич. температуры, плотность системы снизиться за счёт термич. расширения среды. Плотность частицы останется неизменной.
Дата добавления: 2018-05-02; просмотров: 775; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
