Производная функции и ее применение к исследованию функции
Непрерывные функции
Определение 1. Функция 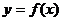 называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и некоторой ее окрестности, существует
, если она определена в этой точке и некоторой ее окрестности, существует  и этот предел равен значению функции в этой точке
и этот предел равен значению функции в этой точке  , т.е.
, т.е.
 .
.
Пример. Проверим непрерывность функции  в произвольной точке
в произвольной точке  :
:
 .
.
Приращением переменной величины будем называть разность между двумя ее различными значениями. Пусть в начальный момент времени переменная величина имела значение  , а затем в процессе своего изменения приняла какое-то значение
, а затем в процессе своего изменения приняла какое-то значение  , разность
, разность  называется приращением этой переменной величины и обозначается
называется приращением этой переменной величины и обозначается  .
.
Приращение функции  соответствует взятому приращению аргумента.
соответствует взятому приращению аргумента.
Определение 2. Функция 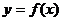 называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента
, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  .
.
Теорема 1. Если функции  и
и  непрерывны в точке
непрерывны в точке  , то их сумма
, то их сумма  , разность
, разность  , произведение
, произведение  и частное
и частное  также непрерывны в этой точке.
также непрерывны в этой точке.
Теорема 2. Если промежуточный аргумент  непрерывен в точке
непрерывен в точке  , а заданная функция
, а заданная функция 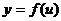 непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке  .
.
Теорема 3. Всякая элементарная функция непрерывна в любой точке своей области определения.
Если в точке  нарушены условия непрерывности функции
нарушены условия непрерывности функции  , то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
, то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
|
|
|
Определение. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной этой функции
 .
.
Геометрический смысл производной
Производная  в некоторой точке
в некоторой точке  равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной в точке касания
равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной в точке касания  к графику функции
к графику функции 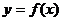 .
.
Уравнение касательной имеет вид:
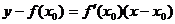
Физические интерпретации производной
Производная пути по времени = скорость движения  .
.
Производная скорости по времени – ускорение движения  .
.
Основные свойства производной
1. Постоянный множитель можно выносить за знак производной

2. Производная суммы нескольких функций равна сумме соответствующих производных слагаемых

Следствие. Производная разности есть разность производных

3. Производная произведения равна произведению производной первого множителя на второй плюс произведение производной второго множителя на первый

4. Дифференцирование частного:

5. Дифференцирование сложной функции
Производная сложной функции по независимой переменной равна производной заданной функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной
|
|
|

Таблица производных
1.  9.
9. 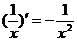
2.  10.
10. 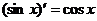
3.  11.
11. 
4. 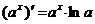 12.
12. 
5.  13.
13. 
6.  14.
14. 
7.  15.
15. 
8.  16.
16. 
17. 
Пример 1. 

 .
.
Пример 2. 
 .
.
Дифференциал функции
Дифференциалом функции 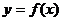 в точке
в точке  называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента
называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента 
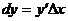 или
или 
Приложения производной к исследованию функции
1. Признак возрастания и убывания функции
Теорема. Если функция 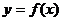 дифференцируема во всех точках какого-то интервала и ее производная
дифференцируема во всех точках какого-то интервала и ее производная  положительна в каждой точке, то функция возрастает на этом интервале. Если производная
положительна в каждой точке, то функция возрастает на этом интервале. Если производная  отрицательна, то функция убывает.
отрицательна, то функция убывает.
Пример. Исследовать функцию 


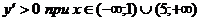 , следовательно, функция
, следовательно, функция  возрастает при
возрастает при  .
.
 , следовательно, функция
, следовательно, функция  убывает при
убывает при  .
.
2. Признаки максимума и минимума.
Теорема (необходимый признак экстремума, признак Ферма). Если в точке экстремума  имеет производную, то производная равна нулю.
имеет производную, то производная равна нулю.
|
|
|
Теорема (достаточный признак экстремума). Если при переходе  через стационарную точку
через стационарную точку  (движение слева направо) производная меняет знак с «+» на «–», то в
(движение слева направо) производная меняет знак с «+» на «–», то в  - максимум, если же с «–» на «+», то
- максимум, если же с «–» на «+», то  - минимум.
- минимум.
В предыдущем примере, точка  - точка максимума, точка
- точка максимума, точка  - точка минимума.
- точка минимума.
3. Наибольшее и наименьшее значения функции на замкнутом интервале
Правило отыскания наибольших и наименьших значений:
1) находим производную исследуемой функции  ;
;
2) определяем критические точки (решаем уравнение 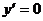 );
);
3) вычисляем значения функции в критических точках и концах интервала;
4) отбираем среди вычисленных значений самое большое и самое малое.
Пример. Найти наибольшее и наименьшее значение функции 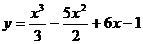 на отрезке [0,10].
на отрезке [0,10].
1) 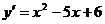 ;
;
2)  . Получили две критические точки (эти точки стационарные, разрывов у
. Получили две критические точки (эти точки стационарные, разрывов у  нет);
нет);
3) составим таблицу значений  в критических точках и в концах интервала:
в критических точках и в концах интервала:

| 0 | 2 | 3 | 10 |

| -1 | 
| 
| 
|
4) наибольшее значение  достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
4. Выпуклость, вогнутость и точки перегиба кривой
|
|
|
Теорема. Если функция 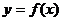 дважды дифференцируема во всех точках какого-то интервала и ее вторая производная
дважды дифференцируема во всех точках какого-то интервала и ее вторая производная  положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная
положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная  отрицательна, то кривая вогнута.
отрицательна, то кривая вогнута.
Теорема (необходимый признак точки перегиба). Если  - точка перегиба, то либо
- точка перегиба, то либо  , либо
, либо  не существует.
не существует.
Теорема (достаточный признак точки перегиба). Если при переходе через точку  вторая производная функции
вторая производная функции  меняет знак, то
меняет знак, то  - точка перегиба.
- точка перегиба.
Пример. 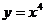
 ;
;
Критическая точка: 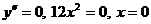
 для всех
для всех  , следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
, следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
5. Асимптоты
Прямая L называется асимптотой кривой, если расстояние от текущей точки М на кривой до прямой L становится бесконечно малой величиной, когда точка М неограниченно удаляется от начала координат (т.е. когда расстояние от М до начала координат  ).
).
Вертикальные асимптоты могут образовываться только в точках бесконечного разрыва функции 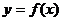 .
.
Пример. Определить вертикальные асимптоты функции  .
.
Данная функция имеет точку разрыва х=2,  ,
,  . Таким образом, прямая х=2 – вертикальная асимптота.
. Таким образом, прямая х=2 – вертикальная асимптота.
Наклонные асимптоты
Пусть прямая L есть наклонная асимптота графика функции 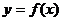 . Теперь точка
. Теперь точка  может уходить на неограниченное расстояние от начала координат, лишь когда
может уходить на неограниченное расстояние от начала координат, лишь когда  (надо, как правило, отдельно разбирать случаи
(надо, как правило, отдельно разбирать случаи  и
и  ). Уравнение наклонной асимптоты к кривой
). Уравнение наклонной асимптоты к кривой 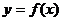 имеет вид:
имеет вид:
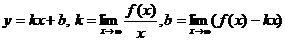 .
.
Пример. Найти асимптоты линии 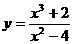
Знаменатель дроби обращается в нуль в точках  . Проверим, будут ли вертикальные прямые
. Проверим, будут ли вертикальные прямые  асимптотами:
асимптотами:
 .
.
Таким образом, прямые  являются вертикальными асимптотами.
являются вертикальными асимптотами.
Найдем наклонные асимптоты:

 =
=
 .
.
Таким образом, наклонная асимптота  .
.
Правило Лопиталя
Теорема (правило Лопиталя). Отыскивается  при
при  или
или  , когда одновременно
, когда одновременно  или
или  (
( 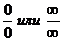 ). Если существует предел (конечный или бесконечный) отношения производных
). Если существует предел (конечный или бесконечный) отношения производных  , то существует и предел отношения функций и эти пределы равны:
, то существует и предел отношения функций и эти пределы равны:
 .
.
Пример.

Общая схема исследования функции. Построение графика
1. Элементарное исследование: область определения; точки разрыва и интервалы непрерывности; точки пересечения графика с осями координат; симметрия графика: четность, нечетность; вертикальные и наклонные асимптоты.
2. Исследование на возрастание, убывание и точки экстремума с помощью производной функции.
3. Выпуклость, вогнутость и точки перегиба – с помощью второй производной.
4. Построение графика.
Неопределенный интеграл
Функия  называется первообразной для функции
называется первообразной для функции  на промежутке Х, если в каждой точке х этого промежутка справедливо равенство
на промежутке Х, если в каждой точке х этого промежутка справедливо равенство  .
.
Совокупность всех первообразных для функции  на промежутке Х называется неопределенным интегралом от функции
на промежутке Х называется неопределенным интегралом от функции  и обозначается
и обозначается  , где С – произвольная постоянная. В записи
, где С – произвольная постоянная. В записи 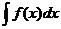 функция
функция  называется подинтегральной функцией, а
называется подинтегральной функцией, а  - подинтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрирования и дифференцирования взаимно обратны.
- подинтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрирования и дифференцирования взаимно обратны.
Основные свойства неопределенного интеграла
1. 
2. 
3. 
4.  , где
, где 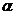 - некоторое число
- некоторое число
5. 
Табличные интегралы
1. 
2.  , где
, где 
3. 
4.  , где
, где 
5. 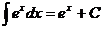
6. 
7. 
8.  , где
, где 
9. 
10. 
11. 
12. 
13. 
Методы интегрирования
Основное содержание различных методов нахождения интегралов состоит в сведении искомого интеграла к табличному или сумме интегралов. В простейших случаях это удается сделать, используя лишь эквивалентные преобразования подынтегральной функции и, если необходимо, свойства интегралов.
1. Метод замены переменной
Пусть  - функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда
- функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда
 .
.
Эта формула называется формулой замены переменной в неопределенном интеграле.
Пример 1. Найти интеграл  .
.
Решение. Сделаем замену  , тогда
, тогда 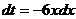 , следовательно
, следовательно  .
.
Тогда  .
.
2. Метод интегрирования по частям
Пусть  и
и  - непрерывно дифференцируемые функции. Тогда справедлива формула:
- непрерывно дифференцируемые функции. Тогда справедлива формула:
 .
.
Эта формула называется формулой интегрирования по частям.
Пример 2. Найти интеграл  .
.
Решение. Пусть  ,
,  . Тогда
. Тогда  ,
, 
Применяя формулу интегрирования по частям, получаем
 .
.
Для нахождения последнего интеграла вновь применим формулу интегрирования по частям, сделаем замену  ,
,  . Тогда
. Тогда  ,
,  .
.
Тогда  .
.
Следовательно, искомый интеграл равен
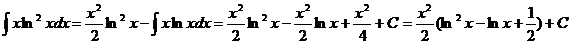 .
.
3. Интегрирование рациональных выражений
Рассмотрим способы нахождения интегралов вида  , где
, где  и
и 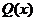 - некоторые многочлены от переменной х.
- некоторые многочлены от переменной х.
Пусть знаменатель 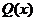 допускает разложение на линейные множители:
допускает разложение на линейные множители:
 ,
,
где  при
при  и
и  - положительные целые числа. В этом случае дробь
- положительные целые числа. В этом случае дробь  допускает представление в виде суммы простейших дробей:
допускает представление в виде суммы простейших дробей:
 ,
,
где  - некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.
- некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.
В случае, когда многочлен 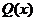 не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида
не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида  , тогда разложение дроби
, тогда разложение дроби  дополнительно содержит слагаемые вида
дополнительно содержит слагаемые вида
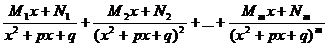
Пример 3. Найти интеграл  .
.
Решение. Разложим подинтегралную функцию на простейшие дроби:

 .
.
Таким образом,  , т.е.,
, т.е.,

Разложение подынтегральной функции имеет вид:
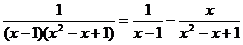 .
.
 .
.
Для первого интеграла преобразуем функцию под знаком дифференцила:  , для второго – выделим полный квадрат в знаменателе
, для второго – выделим полный квадрат в знаменателе  и воспользуемся заменой переменной
и воспользуемся заменой переменной  , тогда
, тогда  .
.
Тогда,


 .
.
Определенный интеграл
Пусть функция 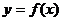 задана на отрезке
задана на отрезке  . Разобьем отрезок
. Разобьем отрезок  на
на  элементарных отрезков точками
элементарных отрезков точками  .
.
В каждом из отрезков разбиения  выберем произвольно точку
выберем произвольно точку 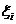 и положим
и положим  . Тогда сумма вида
. Тогда сумма вида
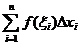
называется интегральной суммой для функции 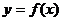 на отрезке
на отрезке  .
.
Пусть существует и конечен предел S интегральной суммы при стремлении к нулю длины максимального элементарного отрезка  , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка  на части и способа выбора точек
на части и способа выбора точек 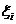 на отрезках разбиения. Тогда функция
на отрезках разбиения. Тогда функция 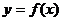 называется интегрируемой на
называется интегрируемой на  , а число S – определенным интегралом от
, а число S – определенным интегралом от  на
на  и обозначается
и обозначается  .
.
Свойства определенного интеграла
1) 
2) 
3) 
4) 
5) 
6)  , если функция
, если функция 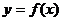 четная
четная
 , если функция
, если функция 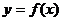 нечетная
нечетная
7) Формула Ньютона-Лейбница

Геометрические приложения определенного интеграла
1. Если функция 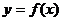 неотрицательна на отрезке
неотрицательна на отрезке  , то площадь S под кривой
, то площадь S под кривой 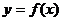 на
на  (площадь криволинейной трапеции, ограниченной кривой
(площадь криволинейной трапеции, ограниченной кривой 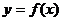 и прямыми
и прямыми  ) численно равна определенному интегралу от
) численно равна определенному интегралу от  на данном отрезке:
на данном отрезке:

(геометрический смысл определенного интеграла)
2. Если функция 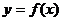 неположительна на отрезке
неположительна на отрезке  , то площадь S над кривой
, то площадь S над кривой 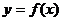 на
на  численно равна определенному интегралу от
численно равна определенному интегралу от  на данном отрезке, взятому со знаком «минус»:
на данном отрезке, взятому со знаком «минус»:

3. Если  на отрезке
на отрезке  , то площадь S фигуры, заключенной между кривыми
, то площадь S фигуры, заключенной между кривыми  и
и  на этом отрезке определяется формулой
на этом отрезке определяется формулой
 .
.
Дата добавления: 2018-05-02; просмотров: 346; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
