Предел последовательности, предел функции
В математике под множеством называется совокупность, набор каких-либо предметов (объектов). Это не есть точное математическое определение. Также как и понятия точки, прямой, числа и т.д., понятие множества является одним из тех первоначальных, наиболее общих понятий, которые принимаются без определения.
Предметы, составляющие множество, называются элементами множества. То, что элемент  входит во множество А, записывается так:
входит во множество А, записывается так:  (читается так: элемент
(читается так: элемент  принадлежит множеству А). Запись
принадлежит множеству А). Запись  означает, что элемент
означает, что элемент  не принадлежит множеству А. Множество, не содержащее ни одного элемента, называется пустым.
не принадлежит множеству А. Множество, не содержащее ни одного элемента, называется пустым. 

Множество можно задать
1) перечислением его элементов (например, множество учеников в классе задается перечислением фамилий в классном журнале);
2) указанием некоторого свойства, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества (например, множество {2,4} может быть задано таким свойством: множество четных чисел, удовлетворяющих неравенству 1<x<5).
Если А и В два множества, то запись А=В означает, что они состоят из одних и тех же элементов. Если каждый элемент множества А является в то же время элементом множества В, то говорят, что А – подмножество В, и пишут:  . Например, множество учеников 10-го класса данной школы есть подмножество множества всех учеников этой школы.
. Например, множество учеников 10-го класса данной школы есть подмножество множества всех учеников этой школы.
|
|
|
Определение. Если одновременно с отношением  имеет место отношение
имеет место отношение  , то множества А и В называются равными, т.е. А=В.
, то множества А и В называются равными, т.е. А=В.
Отношения над множествами иллюстрируются с помощью диаграмм Венна. Диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству.
Пусть дано какое-либо множество Е. мы будем рассматривать всевозможные подмножества данного множества Е. Исходное множество в таком случае называют универсальным множеством.
Пусть множество А есть некоторое подмножество универсального множества Е, тогда множество  , состоящее из всех элементов множества Е, не принадлежащих множеству А, называется дополнением множества А. например, если А – множество всех девочек в классе, то
, состоящее из всех элементов множества Е, не принадлежащих множеству А, называется дополнением множества А. например, если А – множество всех девочек в классе, то  - множество всех мальчиков того же класса.
- множество всех мальчиков того же класса.
Операции над множествами
1. Объединение двух множеств А и В – это множество С, состоящее из всех элементов, принадлежащих или множеству А, или множеству В.
Обозначается  .
.
2. Пересечение двух множеств А и В – это множество С, состоящее из элементов, принадлежащих множеству А и В одновременно.
Обозначается  .
.
3. Разность двух множеств А и В – это множество С, состоящее из всех элементов А, не входящих в В.
|
|
|
Обозначается  .
.
Функции. График функции. Элементарные функции
Определение. Функцией (числовой функцией) называется отображение числового множества D в числовое множество Е.
Функцию записывают так: 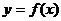 . Множество D называется областью определения функции, а его элемент
. Множество D называется областью определения функции, а его элемент  - аргументом. Множество Е называется областью значений функции, а его элемент
- аргументом. Множество Е называется областью значений функции, а его элемент  - функцией (значением функции, зависимой переменной).
- функцией (значением функции, зависимой переменной).
Для того, чтобы функция была определена, надо знать: а) область определения D; б) закон, по которому каждому числу  ставится в соответствие число
ставится в соответствие число  . Как следует из определения функции, каждому
. Как следует из определения функции, каждому  соответствует только одно
соответствует только одно  , но это вовсе не исключает того, что разным значениям
, но это вовсе не исключает того, что разным значениям  могут соответствовать одинаковые значения
могут соответствовать одинаковые значения  . Закон, по которому задается функция, можно задать разными способами: формулой (аналитический способ), графиком (графический способ), таблицей (табличный способ), словесной формулировкой.
. Закон, по которому задается функция, можно задать разными способами: формулой (аналитический способ), графиком (графический способ), таблицей (табличный способ), словесной формулировкой.
Графиком функции 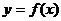 называют множество точек на плоскости, у которых абсциссы являются допустимыми значениями аргумента
называют множество точек на плоскости, у которых абсциссы являются допустимыми значениями аргумента  , а ординаты – соответствующими значениями функции
, а ординаты – соответствующими значениями функции  .
.
График функции представляет собой некоторую кривую на плоскости.
|
|
|
К основным элементарным функциям относятся следующие:
1. Степенная функция  (
(  - постоянное действительное число). При
- постоянное действительное число). При  =0 степенная функция есть постоянная величина
=0 степенная функция есть постоянная величина  ; при
; при  =1 получается функция
=1 получается функция  (прямая пропорциональная зависимость); если
(прямая пропорциональная зависимость); если  =2, то степенная функция
=2, то степенная функция  является квадратичной; если
является квадратичной; если  =-1, то получается обратно пропорциональная зависимость
=-1, то получается обратно пропорциональная зависимость  .
.
2. Показательная функция  (
(  - положительное число,
- положительное число, 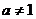 ). Особую роль в математике играет показательная функция с основанием
). Особую роль в математике играет показательная функция с основанием  , то есть функция
, то есть функция  . Число
. Число  - иррациональное число,
- иррациональное число,  =2,718281828459… Функцию
=2,718281828459… Функцию  называют экспоненциальной функцией.
называют экспоненциальной функцией.
3. Логарифмическая функция  (
(  - положительное число,
- положительное число, 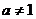 ). На практике часто используют логарифмы по основанию
). На практике часто используют логарифмы по основанию  =10 – десятичные логарифмы. Для десятичного логарифма принята запись
=10 – десятичные логарифмы. Для десятичного логарифма принята запись  . Основание
. Основание  также играет особую роль, логарифм по основанию
также играет особую роль, логарифм по основанию  обозначают следующим образом:
обозначают следующим образом:  и называют натуральным логарифмом числа
и называют натуральным логарифмом числа  .
.
4. Тригонометрические функции 
 .
.
5. Обратные тригонометрические функции 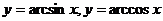 ,
,
 .
.
Функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (сложения, вычитания, умножения и деления) и операций «взятие функции от функции», называются элементарными функциями. Операцию «взятие функции от функции» также называют композицией функций. Функция, в которой вместо переменной записана другая элементарная функция называется сложной функцией и также относится к множеству элементарных функций.
|
|
|
Понятие числовой последовательности и ее предела
Если каждому натуральному числу  по некоторому закону поставлено в соответствие определенное действительное число, то говорят, что задана числовая последовательность
по некоторому закону поставлено в соответствие определенное действительное число, то говорят, что задана числовая последовательность 
Числа  называются членами последовательности;
называются членами последовательности;  называют общим членом последовательности.
называют общим членом последовательности.
Пример последовательности:

Введем понятие предела числовой последовательности. Число А называется пределом числовой последовательности  , если для любого как угодно малого положительного числа
, если для любого как угодно малого положительного числа  существует номер N такой, что все члены последовательности
существует номер N такой, что все члены последовательности  с номерами n>N удовлетворяют следующему неравенству:
с номерами n>N удовлетворяют следующему неравенству:
 .
.
Обозначения:  или
или 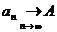 .
.
Определение. Последовательность  называется сходящейся, если она имеет (конечный) предел, и расходящейся, если она предела не имеет.
называется сходящейся, если она имеет (конечный) предел, и расходящейся, если она предела не имеет.
Теорема (критерий Коши, необходимое и достаточное условие сходимости последовательности). Для сходимости последовательности  необходимо и достаточно, чтобы для любого числа
необходимо и достаточно, чтобы для любого числа  существовал номер N такой, что для всех m, n>N выполнялось неравенство
существовал номер N такой, что для всех m, n>N выполнялось неравенство  .
.
Последовательность  , удовлетворяющая условию Коши, называется фундаментальной.
, удовлетворяющая условию Коши, называется фундаментальной.
Теорема (единственной предела последовательности). Последовательность не может иметь двух различных пределов.
Арифметические операции над сходящимися последовательностями
Теорема 1. Если последовательности  и
и  сходятся, то сходится и последовательности
сходятся, то сходится и последовательности  , причем
, причем

Теорема 2. Если последовательности  и
и  сходятся, то сходится и последовательности
сходятся, то сходится и последовательности  , причем
, причем

Теорема 3. Если последовательности  и
и  сходятся, то сходится и последовательности
сходятся, то сходится и последовательности 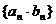 , причем
, причем

Теорема 4. Если последовательности  и
и  сходятся, причем
сходятся, причем  для любого
для любого  и
и  , то последовательность
, то последовательность  также сходится и
также сходится и
 .
.
Предел функции
Определение. Переменная величина стремится к пределу  (
(  - постоянное число), если абсолютная величина
- постоянное число), если абсолютная величина  становится в процессе изменения переменной величины сколь угодно малой.
становится в процессе изменения переменной величины сколь угодно малой.
Предел функции при 
Пусть функция 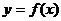 задана на некотором интервале
задана на некотором интервале  .
.
Определение. Число  называется пределом
называется пределом  при
при  , если для любого
, если для любого  существует число
существует число  такое, что для любого
такое, что для любого  выполняется неравенство
выполняется неравенство  .
.
Предел функции при 
Пусть функция  определена во всех точках некоторого интервала
определена во всех точках некоторого интервала  , содержащего точку
, содержащего точку  , кроме, может быть, самой точки
, кроме, может быть, самой точки  .
.
Определение. Число называется пределом функции  в точке
в точке  (при
(при  ), если для любого (сколь угодно малого) положительного числа
), если для любого (сколь угодно малого) положительного числа  существует такое положительное число
существует такое положительное число 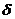 , зависящее от
, зависящее от  , что для всех
, что для всех  из
из 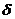 - окрестности точки
- окрестности точки  , исключая, быть может, саму точку
, исключая, быть может, саму точку  (т.е. для всех
(т.е. для всех  , для которых выполняется неравенство
, для которых выполняется неравенство  ), будет выполняться неравенство
), будет выполняться неравенство  .
.
Замечательные пределы
В математике важную роль играют два специальных предела, которые ввиду их важности названы «замечательными»:
 - первый замечательный предел
- первый замечательный предел
 - второй замечательный предел
- второй замечательный предел
Пример 1.
 (здесь введена новая переменная
(здесь введена новая переменная  ).
).
Пример 2. 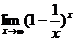 . Положим
. Положим  .
.
Получаем
 .
.
Раскрытие неопределенностей
Иногда правила предельного перехода непосредственно неприменимы. Например, при отыскании  , когда
, когда  и
и  или одновременно
или одновременно  и
и  . В этом случае надо проделать над дробью некоторые преобразования. Чтобы обозначить такие ситуации, говорят, что имеем дело с неопределенностью
. В этом случае надо проделать над дробью некоторые преобразования. Чтобы обозначить такие ситуации, говорят, что имеем дело с неопределенностью 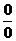 или
или  , а вычисление предела называют «раскрытием неопределенности».
, а вычисление предела называют «раскрытием неопределенности».
Пример 1.  .
.
Пример 2. 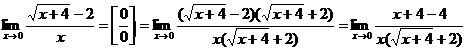 =
=
 . (Чтобы убрать корни, умножили числитель и знаменатель на величину
. (Чтобы убрать корни, умножили числитель и знаменатель на величину  , сопряженную числителю).
, сопряженную числителю).
Пример 3.  . (Поделили числитель и знаменатель дроби на старшую степень
. (Поделили числитель и знаменатель дроби на старшую степень 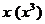 ).
).
«Неопределенности» могут возникнуть и при вычислении предела произведения  . Условно это записывается
. Условно это записывается  . Такую неопределенность легко преобразовать к
. Такую неопределенность легко преобразовать к 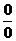 или
или  . Могут возникнуть также неопределенности вида
. Могут возникнуть также неопределенности вида  .
.
Пример 4. 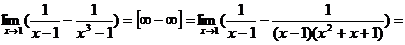
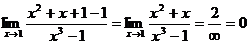 .
.
Сравнение бесконечно малых
Пусть 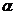 и
и  бесконечно малые (последовательности или функции).
бесконечно малые (последовательности или функции).
1) Если конечный и отличный от нуля предел существует
 ,
,
то говорят, что 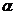 и
и  являются бесконечно малыми (б.м.) одного и того же порядка.
являются бесконечно малыми (б.м.) одного и того же порядка.
2) Если  , то
, то 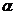 имеет высший порядок малости по отношению к
имеет высший порядок малости по отношению к  (или
(или 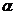 - б.м. более высокого порядка, чем
- б.м. более высокого порядка, чем  ).
).
3) Если  , то
, то  имеет высший порядок малости по отношению к
имеет высший порядок малости по отношению к 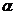 (или -
(или -  б.м. более высокого порядка, чем
б.м. более высокого порядка, чем 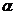 ).
).
4) Если  , то две бесконечно малые
, то две бесконечно малые 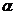 и
и  называются эквивалентными.
называются эквивалентными.
Таблица эквивалентных бесконечно малых при 
1.  6.
6. 
2.  7.
7. 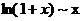
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Пример. 
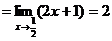 .
.
Дата добавления: 2018-05-02; просмотров: 378; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
