Аналитическая геометрия в пространстве
Плоскость в пространстве и ее уравнения
Пусть в пространстве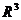 
введена прямоугольная система координат OXYZ. Рассмотрим в пространстве некоторую плоскость Q. Поверхности Q соответствует некоторое уравнение 
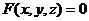. Поверхность, определяемая этим уравнением есть геометрическое место точек в пространстве 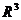, координаты которых x, y, z удовлетворяют этому уравнению. Это означает, что данному уравнению удовлетворяют координаты x, y, z каждой точки, лежащей на поверхности Q, и не удовлетворяют координаты никакой точки, не лежащей на ней. Уравнение 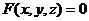называется уравнением данной поверхности Q.
1. Общее уравнение плоскости
,
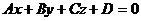где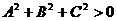 
.
Уравнение плоскости, в котором хотя бы один из коэффициентов А, В, С или D равен нулю, называется неполным уравнением плоскости.
2. Уравнение плоскости, проходящей через точку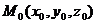 
с данным вектором нормали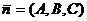 
Вектором нормали к плоскости 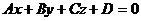называется ненулевой вектор 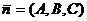, перпендикулярный к данной плоскости имеет вид:
.
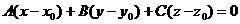3. Уравнение плоскости в отрезках
,
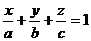где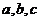 
- это координаты точек 
, 
, 
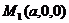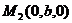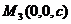, лежащих на координатных осях.
4. Уравнение плоскости, проходящей через три точки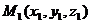 
, 
, 
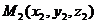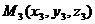
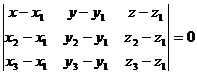
Пример 1. Составить уравнение плоскости, проходящей через три точки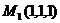 
, 
, 
.
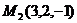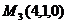Решение.
; 
;
;
;
;
.
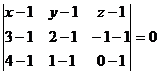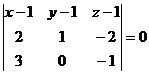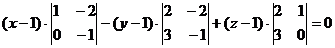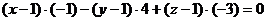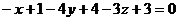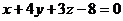Пример 2. Составить уравнение плоскости с нормальным вектором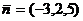 
, проходящей через точку 
.
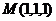Решение. ;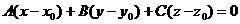
; 
;
.
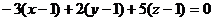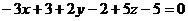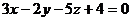Прямая и ее уравнения в пространстве
1. Параметрические уравнения прямой в пространстве
|
|
|
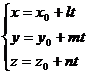
2. Каноническое уравнение прямой в пространстве
.
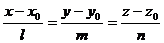Вектор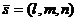 
- направляющий вектор прямой (вектор, параллельный данной прямой).
3. ,Общее уравнение прямой (прямая как пересечение двух плоскостей)
Рассмотрим две плоскости
;
.
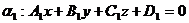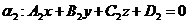Тогда уравнение прямой как линии пересечения двух плоскостей имеет вид:
.
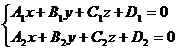Расстояние от точки до прямой
Пусть дана плоскость 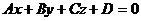и точка 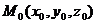. Расстояние 
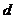от точки 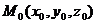до плоскости вычисляется по формуле:
.
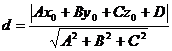Угол между плоскостями
Углом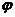 
между двумя плоскостями
;
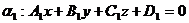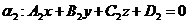
Считается угол между их нормалями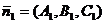 
и 
:
= 
.
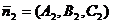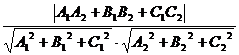Отсюда получим условие перпендикулярности двух плоскостей:
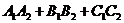=0.
Условие параллельности двух плоскостей:
.
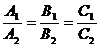Угол между двумя прямыми в пространстве
Пусть заданы канонические уравнения двух прямых:
;
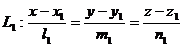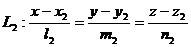
Тогда острый угол 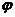между прямыми определяется как угол между их направляющими векторами и вычисляется следующим образом:
= 
.
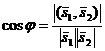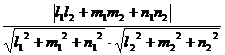Условие перпендикулярности прямых:
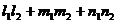=0.
Условие параллельности двух прямых:
.
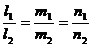Угол между прямой и плоскостью
Острый угол 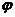между прямой и плоскостью определяется по формуле:
= 
.
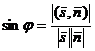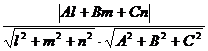Условие параллельности прямой и плоскости:
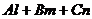=0.
Условие перпендикулярности прямой и плоскости:
|
|
|
.
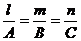Раздел 3. Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной
Дата добавления: 2018-05-02; просмотров: 220; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!