Векторы на плоскости и в пространстве
Существует две категории величин: скалярные и векторные величины. Скалярные величины – это величины, которые определяются только числовым значением (например, масса, температура, объем); векторные величины – это величины, для определения которых необходимо знать не только числовое значение, но и направление (например, сила, ускорение, скорость).
Векторную величину можно задать в виде направленного отрезка – вектора. Вектор может быть обозначен прописной латинской буквой 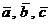 и т.д., или двумя заглавными латинскими буквами
и т.д., или двумя заглавными латинскими буквами 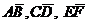 и т.д.
и т.д.
Нулевой вектор – это вектор, начало и конец которого совпадают.
Нулевой вектор не имеет определенного направления.
Длина вектора – это длина отрезка его содержащая.
Векторы, лежащие на параллельных прямых (или на одной и той же прямой), называются коллинеарными.
Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы), или противоположенное направление (противоположено направленные векторы).
Два вектора 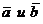 равны, если они сонапрвлены и имеют одну и ту же длину.
равны, если они сонапрвлены и имеют одну и ту же длину.
Линейные операции над векторами
1. Сумма векторов
Определение. Суммой векторов 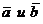 называется такой вектор
называется такой вектор 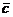 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 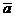 , а конец – с концом вектора
, а конец – с концом вектора 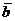 (правило треугольника).
(правило треугольника).
Из определения следует, что сумма двух противоположных векторов равна нулевому вектору: 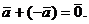
Сложение векторов подчиняется следующим законам:
|
|
|
а) переместительному закону
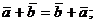
б) сочетательному закону
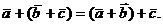
Операция сложения может быть распространена на любое число слагаемых векторов.
Для того чтобы сложить n векторов, надо к концу первого вектора приложить начало второго, затем к концу второго вектора приложить начало третьего и т.д. и, наконец, приложить к концу предпоследнего вектора начало последнего; тогда замыкающий вектор, соединяющий начало первого вектора с концом последнего, и будет являться вектором-суммой данных векторов.
При сложении векторов можно любым образом переставлять и группировать слагаемые.
2. Вычитание векторов
Определение. Разностью векторов 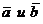 называется такой вектор
называется такой вектор 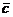 , для которого
, для которого 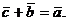
3. Умножение вектора на число (скаляр)
Определение. Произведением вектора 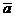 на число (скаляр)
на число (скаляр) 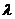 называется вектор, длина которого равна
называется вектор, длина которого равна 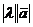 , сонаправленный с вектором
, сонаправленный с вектором 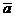 , если
, если 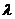 >0, и противоположено направленный, если
>0, и противоположено направленный, если 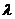 <0.
<0.
Умножение вектора на число подчиняется законам:
а) сочетательному закону
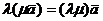 ;
;
б) распределительному закону
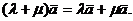
4. Скалярное произведение векторов
Определение. Скалярным произведением вектора 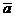 на вектор
на вектор 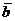 называется число, равное произведению их длин (модулей) на косинус угла между ними:
называется число, равное произведению их длин (модулей) на косинус угла между ними:
|
|
|
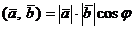 .
.
Скалярное произведение можно записать в виде
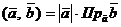 .
.
Утверждение. Скалярное произведение ненулевых векторов 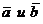 равно нулю, если векторы перпендикулярны (ортогональны), и наоборот.
равно нулю, если векторы перпендикулярны (ортогональны), и наоборот.
Скалярное произведение обладает следующими свойствами:
1) 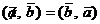 - переместительный закон
- переместительный закон
2) 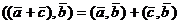 - распределительный закон
- распределительный закон
3) 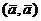 называется скалярным квадратом вектора
называется скалярным квадратом вектора 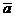 , обозначается
, обозначается 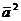
4) 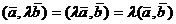 - числовой множитель можно вынести за знак скалярного произведения
- числовой множитель можно вынести за знак скалярного произведения
5. Векторное произведение векторов.
Определение. Векторным произведением векторов 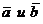 называется вектор
называется вектор 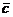 , удовлетворяющий следующим условием:
, удовлетворяющий следующим условием:
1) 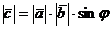 , где
, где 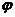 - угол между векторами
- угол между векторами 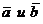 ;
;
2) 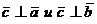 , то есть вектор
, то есть вектор 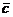 перпендикуляр плоскости, «натянутой» на векторы
перпендикуляр плоскости, «натянутой» на векторы 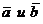
3) векторы 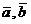 и
и 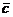 (после их приведения к общему началу) ориентированы по отношению друг к другу, соответственно, как орты
(после их приведения к общему началу) ориентированы по отношению друг к другу, соответственно, как орты 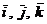 , т.е. образуют так называемую «правую» тройку векторов.
, т.е. образуют так называемую «правую» тройку векторов.
Векторное произведение 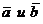 обозначается так:
обозначается так: 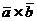 или
или 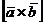 .
.
Свойства векторного произведения
1) 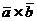 =-
=- 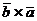 , т.е. векторное произведение не обладает переместительным свойством, то есть при перестановке сомножителей векторное произведение меняет направление;
, т.е. векторное произведение не обладает переместительным свойством, то есть при перестановке сомножителей векторное произведение меняет направление;
2) 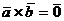 , если
, если 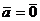 или
или 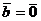 , либо
, либо 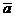 ǁ
ǁ 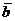 ;
;
3) 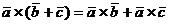 - распределительный закон;
- распределительный закон;
4) 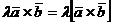 - сочетательный закон по отношению к скалярному множителю;
- сочетательный закон по отношению к скалярному множителю;
|
|
|
5) 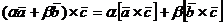 - линейность по первой компоненте. Аналогично, справедлива линейность и по второй компоненте.
- линейность по первой компоненте. Аналогично, справедлива линейность и по второй компоненте.
Модуль векторного произведения (длина вектора 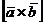 численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 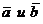 ).
).
6. Смешанное произведение
Определение. Смешанным произведением трех векторов 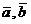 и
и 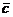 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 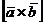 на вектор
на вектор 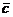 , т.е.
, т.е. 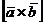 ·
· 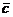 .
.
Свойства смешанного произведения:
1) смешанное произведение трех векторов равно нулю, если:
а) хотя бы один из перемноженных векторов равен нулю;
б) два из перемноженных векторов коллинеарны;
в) все три вектора параллельны одной и той же плоскости (компланарны).
2) смешанное произведение не изменится, если в нем поменять местами знаки векторного (×) и скалярного (·) умножения, т.е.
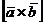 ·
· 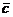 =
= 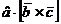 .
.
Объем V треугольной пирамиды, построенной на векторах 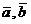 и
и 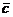 , вычисляется по формуле
, вычисляется по формуле
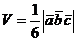 .
.
Прямоугольная система координат на плоскости и в пространстве
Две взаимно перпендикулярные оси ОХ, ОY, проходящие через некоторую точку О, образуют прямоугольную систему координат на плоскости. Три взаимно перпендикулярные оси ОХ, ОY, OZ, проходящие через некоторую точку О, образуют систему координат в пространстве.
|
|
|
При этом точка О называется началом координат, прямые ОХ, ОY (ОХ, ОY, OZ в пространственном случае) – осями координат (ось Ох – ось абсцисс, ось ОY – ось ординат, OZ – ось аппликат). Плоскости ХОY, YOZ, ZOX – координатными плоскостями.
Положение любой точки М в пространстве можно определить тремя числами (координатами) следующим образом: из точки М опустим перпендикуляр MD на плоскость XOY, затем из точки D опустим перпендикуляр DN на ось ОХ, DL – на ось OY. Из точки М опустим перпендикуляр КМ на ось OZ. числа х, у, z «измеряющие» соответственно отрезки ON, OL, OK в выбранном масштабе, называются прямоугольными координатами точки М.
Если точка М имеет координаты х, у, z, то это записывается так: М(х, у, z). Вектор 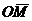 , идущий от начала О к некоторой точке М, называется радиус-вектором точки М. Координаты х, у, z точки М соответственно равны координатам вектора.
, идущий от начала О к некоторой точке М, называется радиус-вектором точки М. Координаты х, у, z точки М соответственно равны координатам вектора.
Каждый вектор равен сумме его вектор-проекций по трем осям координат:
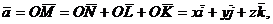
где 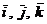 - вектора-орты (единичные векторы, лежащие на осях в прямоугольной системе координат).
- вектора-орты (единичные векторы, лежащие на осях в прямоугольной системе координат).
Тройка векторов 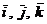 , по которым осуществлено разложение вектора, называется базисом. Представление вектора в виде суммы компонент называется разложением этого вектора по базису
, по которым осуществлено разложение вектора, называется базисом. Представление вектора в виде суммы компонент называется разложением этого вектора по базису 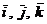 .
.
Длина вектора 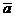 определяется следующим образом:
определяется следующим образом:
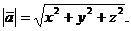
Операции над векторами, заданными в координатной форме
1. Два вектора равны, если их координаты равны.
2. При сложении векторов, заданных в координатной форме, их координаты складываются.
3. При вычитании векторов, заданных в координатной форме, их координаты вычитаются.
4. При умножении вектора на число надо все его координаты умножить на это число.
5. Скалярное произведение векторов 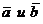 , заданных в координатной форме, определяется числом вида
, заданных в координатной форме, определяется числом вида
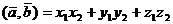 .
.
6. Векторное произведение векторов 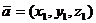 и
и 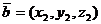 в координатной форме вычисляется следующим образом:
в координатной форме вычисляется следующим образом:
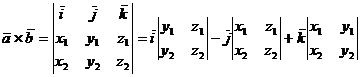 .
.
7. Смешанное произведение в координатной форме вычисляется следующим образом:
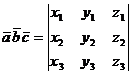 .
.
Пример 1. Даны два вектора 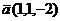 и
и 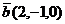 . Найти косинус угла между векторами
. Найти косинус угла между векторами 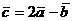 и
и 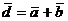 .
.
Решение. Найдем координаты векторов 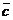 и
и 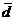 :
:
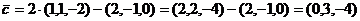 ;
;
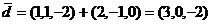 .
.
Вычислим длины векторов 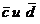 :
:
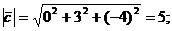
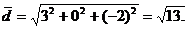
Вычислим косинус угла 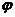 между этими векторами:
между этими векторами:
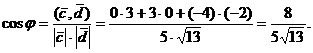
Пример 2. При каком значении 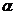 векторы
векторы 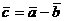 и
и 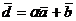 перпендикулярны (ортогональны)? (Координаты векторов
перпендикулярны (ортогональны)? (Координаты векторов 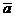 и
и 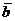 заданы в примере 1).
заданы в примере 1).
Решение. Найдем координаты векторов 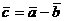 и
и 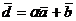 :
:
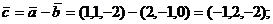
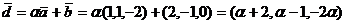 .
.
Запишем условие ортогональности полученных векторов:
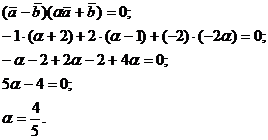
Пример 3. Найти площадь треугольника, построенного на векторах 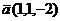 и
и 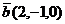 .
.
Решение. Вычислим векторное произведение векторов 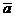 и
и 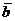 :
:
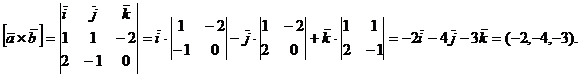 Вычислим модуль векторного произведения по формуле:
Вычислим модуль векторного произведения по формуле: 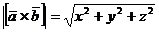 .
.
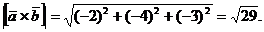
Площадь треугольника равна половине площади параллелограмма
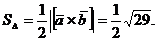
Дата добавления: 2018-05-02; просмотров: 784; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
