Раздел 2. Элементы аналитической геометрии
Nbsp; Жолудева В.В.
МАТЕМАТИКА
(для студентов заочной формы обучения)
Учебное пособие
Содержание
Раздел 1. Линейная алгебра………………………………………………………4
1.1 Матрицы и определители………………………………………4
1.2 Системы линейных уравнений…………………………..........11
Раздел 2. Элементы аналитической геометрии…………………………..........23
2.1 Векторы на плоскости и в пространстве…………………….23
2.2 Аналитическая геометрия на плоскости……………………..27
2.3 Аналитическая геометрия в пространстве…………………...34
Раздел 3. Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной………………………..42
3.1 Предел последовательности, предел функции………………42
3.2 Производная функции и ее применение к исследованию функций………………………………………………………..48
3.3 Неопределенный интеграл……………………………………54
3.4 Определенный интеграл. Несобственный интеграл………...56
Раздел 1. Линейная алгебра
Матрицы и определители
Прямоугольной матрицей порядка m×n называется таблица чисел, состоящая из m строк и n столбцов.

Сокращенно обозначается  .
.
Числа  называются элементами матрицы А.
называются элементами матрицы А.
Если m=n, то матрица называется квадратной, а число n называют порядком матрицы.
Совокупность элементов 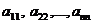 образует главную диагональ квадратной матрицы, а элементы
образует главную диагональ квадратной матрицы, а элементы  - побочную диагональ.
- побочную диагональ.
|
|
|
Так, для матрицы
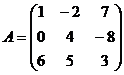
главная диагональ – это числа 1, 4, 3, побочная диагональ – 7, 4, 6.
Нулевой матрицей называют матрицу, все элементы которой равны нулю:

Единичная матрица – это матрица, на главной диагонали которой стоят единицы, все остальные элементы равны нулю:

Квадратная матрица, под главной диагональю которой стоят нули, называется верхнетреугольной; соответственно определяется нижнетреугольная матрица:
 - верхнетреугольная матрица,
- верхнетреугольная матрица,
 - нижнетреугольная матрица.
- нижнетреугольная матрица.
Симметричной называется квадратная матрица, у которой все элементы симметричны относительно главной диагонали.
Действия над матрицами
1. Суммой двух матриц  и
и  одного порядка называется матрица
одного порядка называется матрица  , каждый элемент которой равен сумме соответствующих элементов матриц А и В.
, каждый элемент которой равен сумме соответствующих элементов матриц А и В.
Из определения следует, что выполняются операции коммутативности сложения А+В=В+А и ассоциативности сложения А+(В+С)=(А+В)+С.
2. При умножении матрицы  на число k каждый ее элемент умножается на это число.
на число k каждый ее элемент умножается на это число.
Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.
Операция умножения матрицы на число обладает свойствами:
(α+β)А=αА+β;
|
|
|
α (А+В)= αА+ αВ,
где α и β – числа.
3. Умножение матриц. Пусть заданы матрицы  и
и  .
.
Произведением А×В называется матрица С порядка m×k:
А·В=  ·
·  =С=
=С= 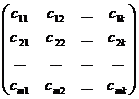
элементы которой вычисляются по формулам:
 ;
;
 и т.д.
и т.д.
Операция перемножения матриц не коммутативна, то есть АВ≠ВА.
4. Транспонирование матрицы - это операция, при которой строки матрицы становятся столбцами, и наоборот.
Пример. Найти матрицу С=В(3А-2В), где А=  и В=
и В=  .
.
Решение. 1) Найдем матрицу (3А-2В)= 3  - 2
- 2  =
=  -
-  =
=  .
.
2) С=В(3А-2В) = 
 =
=  .
.
Элементарные преобразования. Приведение матрицы к ступенчатому виду
1) можно менять строки (столбцы) местами;
2) можно умножать элементы строки на одно и то же число, отличное от нуля;
3) можно складывать (вычитать) строки друг с другом.
Верхнетреугольная матрица, у которой под главной диагональю все элементы равны нулю, называется приведенной к ступенчатому виду. При этом элементы, стоящие на главной диагонали называются угловыми элементами.
Ранг матрицы А – это максимальное число линейно независимых строк этой матрицы.
Утверждение. В ступенчатой матрице строки, содержащие ненулевые угловые элементы, линейно независимы. Отсюда следует, что ранг ступенчатой матрицы равен числу ее угловых элементов.
|
|
|
Приведение матрицы к ступенчатому виду с помощью метода Гаусса
Рассмотрим этот метод на примере матрицы А= 
Поменяем вторую и первую строки местами (для ручного счета удобно, чтобы элемент 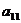 был равен 1 или -1 (если это возможно)).
был равен 1 или -1 (если это возможно)).
Получим матрицу

В дальнейшем первую строку менять не будем. Теперь с помощью элемента 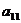 =-1 образуем нули в первом столбце, во второй, третьей и четвертой строках. Для этого ко второй строке прибавим первую, умноженную на число 2, из третьей строки вычтем первую, к четвертой прибавим первую строку:
=-1 образуем нули в первом столбце, во второй, третьей и четвертой строках. Для этого ко второй строке прибавим первую, умноженную на число 2, из третьей строки вычтем первую, к четвертой прибавим первую строку:

Поменяем местами в этой матрице вторую и третью строки, и в дальнейшем первая и вторая строки меняться не будут. И с помощью элемента 1 получим нули во втором столбце в третьей и четвертой строках:

Здесь из третьей строки вычли вторую, умноженную на 5, а из четвертой – вторую, умноженную на 6.
Из четвертой строки вычтем третью, получим матрицу:

Угловые элементы -1, 1, 1, их число равно 3. следовательно, ранг матрицы равен 3.
Справедливы следующие теоремы.
Теорема 1. Элементарные преобразования не меняют ранга матрицы.
Теорема 2. Любую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
|
|
|
Определители
Важной характеристикой квадратной матрицы А порядка n является ее определитель
1. Рассмотрим это понятие для матриц второго порядка.
Пусть задана матрица
 .
.
Определитель матрицы А – число которое ставится в соответствие матрице А и вычисляется по правилу det A=  .
.
Обозначение: det A=  =
=  .
.
Например, det A= 
2. Рассмотрим квадратную матрицу третьего порядка.
Определитель третьего порядка это число
 =
=  .
.
Например,  =
=
= 
3. Определители n-го порядка.
Минор  элемента
элемента  матрицы
матрицы  - это определитель порядка n-1, полученный из матрицы А вычеркиванием i-той строки и j-ого столбца, на пересечении которых стоит этот элемент.
- это определитель порядка n-1, полученный из матрицы А вычеркиванием i-той строки и j-ого столбца, на пересечении которых стоит этот элемент.
Алгебраическое дополнение  отличается от минора лишь знаком:
отличается от минора лишь знаком:
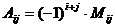 .
.
Определителем матрицы А n-го порядка называется число, полученное разложением по i-й строке:
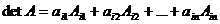 .
.
Пример. Вычислить определитель матрицы 
Вычислим определитель матрицы разложением его по элементам третьей строки (так как эта строка содержит нулевой элемент):
det A=0·А31+(-3)·А32+2·А33+1·А34=-3·А32+2·А33+А34



Тогда, det A=-3·20+2·(-28)-12=-60-56-12=-128.
Основные свойства определителей
1. При умножении всех элементов некоторой строки на число определитель исходной матрицы умножается на это число.
2. Определитель матрицы с нулевой строкой равен нулю
3. При перестановке двух строк определитель меняет знак.
4. Если две строки матрицы равны, то ее определитель равен нулю.
5. Определитель не меняется, если к какой-нибудь строке матрицы прибавить другую ее строку, умноженную на число.
6. Определитель произведения двух матриц равен произведению определителей: 
7. Определитель не меняется при транспонировании матрицы.
Замечание 1. При элементарных преобразования Гаусса определитель матрицы может только изменить знак (при перестановке строк). Поэтому удобно считать определитель матрицы, предварительно приведя ее к ступенчатому виду.
Замечание 2. Преобразование Гаусса сводит квадратичную матрицу к верхнетреугольному виду, определитель которой равен произведению диагональных элементов.
Замечание 3. Если ранг матрицы равен ее порядку, то строки матрицы линейно независимы. Таким образом, равенство нулю определителя есть признак линейной зависимости строк матрицы.
Обратная матрица
Матрица А-1 называется обратной к матрице А, если выполняется условие А· А-1= А-1·А=Е.
Теорема. Матрица А имеет обратную А-1 тогда и только тогда, когда А – невырожденная, det A≠0.
Способы вычисления обратной матрицы
1. Способ вычисления обратной матрицы с помощью алгебраических дополнений.
Алгоритм вычисления:
1) вычисляют определитель матрицы det A;
2) для каждого элемента  вычисляют алгебраические дополнения
вычисляют алгебраические дополнения  ;
;
3) составляют матрицу  из алгебраических дополнений:
из алгебраических дополнений:
 ;
;
4) транспонируют матрицу  :
:

Матрица 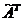 называется присоединенной к матрице А;
называется присоединенной к матрице А;
5) определяют обратную матрицу по формуле:
 .
.
Пример. Найти матрицу, обратную к матрице 
1) det A=0+20-6-0+20+8=42
2) 

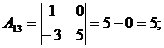
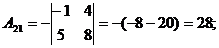
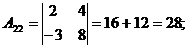




3) 
4)  ;
;
5) 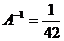
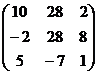 .
.
Сделаем проверку, убедимся, что полученная матрица искомая:
А· А-1= 

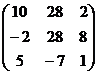 =
=  .
.
2. Метод Гаусса вычисления обратной матрицы.
1) припишем к матрице А единичную матрицу того же порядка:
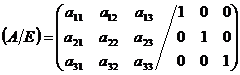 .
.
С помощью элементарных преобразований приведем матрицу  сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица
сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица  .
.
Пример. 

 Итак,
Итак, 
Системы линейных уравнений
Рассмотрим систему m уравнений с n неизвестными
 (1)
(1)
Матрица А, составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1):
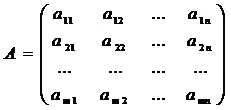
Матрица  называется расширенной матрицей.
называется расширенной матрицей.
Вектор  называется вектором неизвестных, вектор
называется вектором неизвестных, вектор 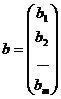 называется вектором свободных членов.
называется вектором свободных членов.
Матричная запись системы (1) имеет вид:

Если вектор b=0, то система называется однородной, если b≠0 (хотя бы один из элементов отличен от нуля), то система называется неоднородной.
Решением системы (1) называется такой вектор X= 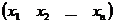 , что при подстановке чисел
, что при подстановке чисел  в систему (1) получаются верные равенства (тождества).
в систему (1) получаются верные равенства (тождества).
Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.
Две системы называются эквивалентными, если множества их решений совпадают. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей 
Однородные системы
Рассмотрим однородную систему  .
.
Заметим, что однородная система всегда совместна, поскольку нуль-вектор Х=  ее решение.
ее решение.
Для решения однородной системы уравнений применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе.
Проиллюстрируем алгоритм метода на примере:

Прямой ход метода Гаусса. Приведем матрицы системы к ступенчатому виду:
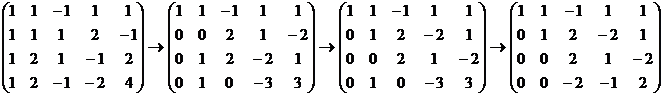
 .
.
Матрица приведена к ступенчатому виду, ее ранг равен 3.
Выпишем соответствующую систему уравнений:

Переменные  , не связанные с угловыми элементами, называются свободными, переменные
, не связанные с угловыми элементами, называются свободными, переменные  - зависимые переменные (несвободные, базисные). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно n-r (r – ранг матрицы).
- зависимые переменные (несвободные, базисные). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно n-r (r – ранг матрицы).
Обратный ход метода Гаусса заключается в том, что зависимые переменные выражаются через свободные из ступенчатой системы, начиная с последнего уравнения и «поднимаясь» вверх к первому. В результате получим
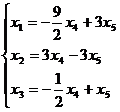
Полученное выражение называют общим решением системы в координатной форме.
Полученные выражения дают описание всего множества решений однородной системы. Давая свободным переменным произвольные значения, и вычисляя значения зависимых переменных, получаем некоторое частное решение системы.
Запишем общее решение в векторной форме. Придадим свободным переменным значения  , получим
, получим  и
и  ; затем
; затем 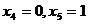 , получим
, получим  и
и  . Векторы
. Векторы  линейно независимы и образуют фундаментальную систему решений (ФСР).
линейно независимы и образуют фундаментальную систему решений (ФСР).
Общее решение системы, записанное в векторной форме, имеет вид:


Неоднородные системы
Пусть задана неоднородная система уравнений

Теорема Кронекера-Капелли (критерий совместности неоднородной системы). Система совместна тогда и только тогда, когда ранг основной матрицы А равен рангу расширенной матрицы  :
:  .
.
Методы решения систем линейных уравнений
1. Метод Гаусса
Рассмотрим на примере системы 
Прямой ход метода Гаусса. Приведем расширенную матрицу системы к ступенчатому виду:
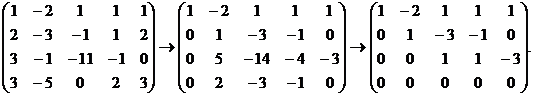
Здесь 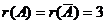 , система совместна.
, система совместна.
Запишем эквивалентную ступенчатую систему:

Переменные  являются зависимыми, а
являются зависимыми, а  - свободной переменной.
- свободной переменной.
Обратный ход метода Гаусса. Выразим зависимые переменные через свободные, получим:
 .
.
Пример 2. Решить систему уравнений методом Гаусса
 .
.
Составим расширенную матрицу и приведем ее к ступенчатому виду:

Запишем эквивалентную ступенчатую систему:

Таким образом, решением данной системы уравнений является вектор  .
.
2. Метод решения системы уравнений с помощью обратной матрицы.

Найдем решение системы уравнений из примера 2 с помощью обратной матрицы. Прежде всего, определим обратную матрицу А-1 с помощью алгебраических дополнений.
det A= 
Для каждого элемента определим алгебраические дополнения:
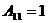 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Тогда, А-1 =  .
.
Решение системы уравнений имеет вид:
Х= 
 .
.
Таким образом, решением данной системы уравнений является вектор  .
.
3. Метод Крамера решения системы уравнений.
Рассмотрим неоднородную систему уравнений  с невырожденной матрицей А (det A≠0):
с невырожденной матрицей А (det A≠0):

Теорема Крамера. Система  , где det A≠0, имеет единственное решение, которое вычисляется по формулам:
, где det A≠0, имеет единственное решение, которое вычисляется по формулам:
 ,
,
где Δ= det A, 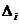 - получается из определителя Δ заменой i-го столбца на столбец свободных членов.
- получается из определителя Δ заменой i-го столбца на столбец свободных членов.
Пример. Найти решение системы уравнений методом Крамера
 .
.
Решение.



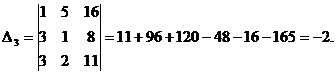
Итак, 
Раздел 2. Элементы аналитической геометрии
Дата добавления: 2018-05-02; просмотров: 279; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
