Задание 4. Действия над векторами
Даны длины двух векторов 
и известен угол между ними 
.
Требуется найти:
1) длину соответствующего вектора в задачах: 1, 4, 7, 10, 13, 16, 19;
2) скалярное произведение в задачах: 2, 5, 8, 11, 14, 17, 20;
3) скалярный квадрат в задачах: 3, 6, 9, 12, 15, 18.
Таблица 3 – Данные задания 4 «Действия над векторами»
| 
| 
| Найти |
|
|
|
| Найти | ||
| 1 | 2 | 3 | 
| 
| 11 | 6 | 4 | 
| 
| |
| 2 | 4 | 2 | 
| 
| 12 | 5 | 2 |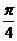 
| 
| |
| 3 | 3 | 4 | 
| 
| 13 | 6 | 2 | 
| 
| |
| 4 | 2 | 4 | 
| 
| 14 | 3 | 6 | 
| 
| |
| 5 | 3 | 2 | 
| 
| 15 | 6 | 5 | 
| 
| |
| 6 | 2 | 5 |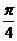
| 
| 16 | 1 | 6 |
| 
| |
| 7 | 5 | 3 |
| 
| 17 | 6 | 3 |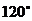 
| 
| |
| 8 | 4 | 3 |
| 
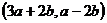
| 18 | 2 | 6 |
| 
| |
| 9 | 4 | 5 |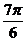 
| 
| 19 | 4 | 6 |
|
| |
| 10 | 5 | 4 |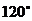
| 
| 20 | 5 | 1 |
| 
|
Пример 4
Найти длину вектора 
, если известно, что 
Решение:
Задание 5. Координаты вектора в новом базисе
Показать, что система векторов 
, , 
образует базис, разложить вектор 
по этому базису. Решить систему уравнений, используя формулы Крамера. Координаты векторов даны в таблице 6.
Таблица 6 – Данные задания 5 «Координаты вектора в новом базисе»
| № | 
| 
| 
| 
|
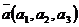
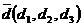
| 1 | (3,1,4) | (-1,-3,1) | (-2,1,-5) | (3,-1,4) |
| 2 | (5,3,3) | (3,-2,2) | (2,4,1) | (9,-5,6) |
| 3 | (1,3,2) | (1,5,2) | (-2,-1,3) | (-1,0,5) |
| 4 | (2,3,3) | (4,1,-4) | (1,2,5) | (3,1,5) |
| 5 | (4,2,1) | (-1,-2,1) | (2,1,2) | (9,3,5) |
| 6 | (1,3,4) | (-3,1,1) | (1,-2,-1) | (-2,-1,3) |
| 7 | (3,1,1) | (1,2,4) | (-2,-1,-5) | (5,3,1) |
| 8 | (1,2,2) | (3,5,-1) | (-2,2,3) | (-1,3,-2) |
| 9 | (2,4,1) | (-1,-2,-3) | (-1,-3,3) | (-1,-3,-2) |
| 10 | (2,3,4) | (2,-2,3) | (-1,2,1) | (-3,1,2) |
| 11 | (2,2,1) | (-3,4,-2) | (2,-5,-3) | (3,-4,-7) |
| 12 | (3,2,1) | (2,1,-4) | (5,3,3) | (6,3,0) |
| 13 | (2,3,1) | (-1,2,-3) | (-1,2,-5) | (3,1,2) |
| 14 | (1,5,2) | (2,3,3) | (4,-4,1) | (3,5,1) |
| 15 | (4,1,2) | (2,2,1) | (-1,1,-2) | (-1,3,1) |
| 16 | (3,1,1) | (-1,4,3) | (-1,-1,-2) | (2,3,-1) |
| 17 | (1,4,2) | (-2,-5,-1) | (3,1,1) | (0,-5,1) |
| 18 | (3,1,5) | (-1,-3,2) | (1,-2,2) | (-2,1,3) |
| 19 | (1,2,3) | (-2,-4,-1) | (1,3,-3) | (1,4,1) |
| 20 | (2,2,3) | (2,3,4) | (-3,2,1) | (-6,5,3) |
|
|
|
Пример 5
Показать, что система векторов 
, 
, 
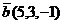образует базис, найти разложение 
в этом базисе.
Решение: Покажем, что векторы 
, , 
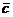образуют базис. Найдём определитель, составленный из координат этих векторов.
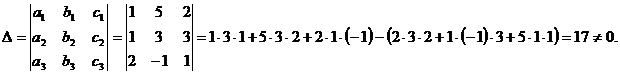
Т.к. определитель не равен нулю, следовательно, векторы линейно независимы и образуют базис.
Разложим вектор 
по векторам данного базиса: 
, здесь 
, 
, 
− искомые координаты вектора 
в базисе 
, 
, 
. В координатной форме это уравнение (1, 1, 2) + 
(5, 3, -1) + 
(2, 3, 1) = (5, 2, 2) принимает вид:
Решим приведённую систему по формулам Крамера 
; для этого вычислим дополнительные определители 
полученные из основного определителя Δ заменой 
–го столбца столбцом свободных членов:
; 
.
Таким образом, находим коэффициенты разложения вектора 
:
Задание 6. Решение задач линейного программирования симплексным методом
Затраты трёх видов сырья А, В, С на производство единицы каждого из трёх типов продукции заданы векторами –
, 
, 
. Запасы каждого вида сырья заданы вектором 
, прибыль от реализации единицы продукции каждого типа − вектором 
. Определить оптимальный план выпуска продукции, при котором прибыль от реализации выпущенной продукции будет максимальной. Составить математическую модель задачи, решить задачу симплексным методом. Составить двойственную задачу к данной и найти её решение.
|
|
|
Таблица 7– Данные задания 6 «Симплексный метод решения задач»
| № |
|
|
|
|
|
| 1 | (3, 2, 4) | (5, 4, 3) | (6, 2, 2) | (270, 90, 190) | (2, 1,1) |
| 2 | (3, 2, 4) | (1, 2, 3) | (5, 4, 1) | (230, 210, 130) | (1, 2, 3) |
| 3 | (3, 2, 4) | (4, 7, 6) | (2, 1, 1) | (230, 270, 190) | (1, 1, 2) |
| 4 | (7, 1, 3) | (1, 2, 1) | (3, 1, 6) | (200, 90, 150) | (3, 1, 2) |
| 5 | (4, 5, 3) | (4, 7, 6) | (2, 1, 1) | (230, 270, 190) | (2, 1, 3) |
| 6 | (2, 5, 4) | (3, 2, 7) | (6, 1, 2) | (190, 140, 100) | (2, 1, 3) |
| 7 | (2, 6, 1) | (8, 4, 3) | (1, 5, 4) | (325, 325, 215) | (1, 3, 2) |
| 8 | (5, 3, 1) | (3, 5, 4) | (2, 1, 3) | (270, 240, 145) | (3, 1, 2) |
| 9 | (4, 1, 3) | (1, 3, 3) | (2, 4, 5) | (200, 120, 260) | (1, 2, 3) |
| 10 | (6, 1, 2) | (9, 1, 1) | (3, 2, 4) | (480, 90, 140) | (2, 5, 4) |
| 11 | (2, 2, 4) | (1, 1, 5) | (3, 5, 1) | (150, 190, 230) | (2, 3, 4) |
| 12 | (4, 2, 5) | (2, 6, 1) | (5, 1, 2) | (200, 150, 160) | (2, 3, 1) |
| 13 | (3, 2, 1) | (5, 3, 4) | (4, 4, 5) | (160, 120, 180) | (2, 1, 3) |
| 14 | (2, 3, 5) | (4, 1, 3) | (3, 8, 1) | (100, 150, 130) | (1, 2, 1) |
| 15 | (3, 7, 2) | (5, 1, 2) | (1, 1, 6) | (125, 165, 150) | (3, 2, 1) |
| 16 | (9, 3, 1) | (4, 3, 5) | (1, 4, 1) | (290, 175, 155) | (1, 2, 1) |
| 17 | (2, 6, 4) | (4, 2, 1) | (1, 3, 5) | (130, 200, 150) | (2, 1, 1) |
| 18 | (1, 4, 2) | (1, 5, 3) | (7, 1, 6) | (175, 170, 210) | (1, 2, 1) |
| 19 | (2, 3, 2) | (2, 3, 4) | (7, 4, 1) | (150, 160, 280) | (1, 1, 2) |
| 20 | (3, 1, 2) | (1, 2, 4) | (5, 3, 1) | (170, 115, 105) | (2, 2, 3) |
Пример 6. Составим математическую модель.
|
|
|
Пусть предприятие выпустит x1 единиц продукции I, х2 единиц продукции II, х3 единиц продукции III.
Расход сырья А на все виды продукции – 
. По условию задачи расход сырья А не должен превышать запаса 
, т.е. 
≤ Аналогично составляем ограничения расхода сырья В и С. Получим систему неравенств:
Прибыль от реализации выпущенной продукции будет равна
.
Запишем модель задачи:
(12)
. (13)
(13) называют целевой функцией.
Пусть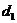 
(7,2,5), d2(0,3,1), d3(5,2,1), Q(220,140,100), Р(2,1,1)
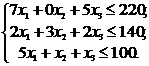(14)
. (15)
|
|
|
Введем балансовые переменные 
, 
, 
в каждое неравенство для приведения модели к каноническому виду
(16)
, (j=1,2,…6)
. (17)
Алгоритм симплексного метода
1. Записываем данную задачу в исходную симплексную таблицу.
2. Если все элементы оценочной строки симплексной таблицы неотрицательны, то соответствующий план является оптимальным.
3. Если в оценочной строке содержится отрицательный элемент, а в столбце над ним нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов и задача не имеет решения.
4. Если в каждом столбце соответствующем отрицательной оценке содержится хотя бы один положительный элемент, то можно перейти к “лучшему ” плану следующим образом:
а) выбираем разрешающий столбец по наименьшей отрицательной оценке;
б) выбираем разрешающую строку по минимальному значению 
;
равно отношению свободных членов к соответствующим положительным элементам разрешающего столбца;
в) на пересечении разрешающего столбца и разрешающей строки лежит разрешающий элемент;
г) элементы разрешающей строки делим на разрешающий элемент и записываем в новой таблице, сохраняя порядок строки, оставшиеся элементы разрешающего столбца заполняем нулями;
д) элементы остальных строк, в том числе и оценочной строки, вычисляем по формулам прямоугольников (см. метод Жордана – Гаусса).
Составим симплексную таблицу.
Таблица заполняется следующим образом:
В столбце “ai0” записываются свободные члены уравнений (16), в столбцах “ x1”, “x2”, …, “x6” − коэффициенты при соответствующих неизвестных этой системы.
В столбце “базис” выписываются базисные переменные, содержащиеся в соответствующих уравнениях системы (16).
Верхняя строчка и крайний левый столбец содержат коэффициенты при соответствующих неизвестных целевой функции Z выражения (17).
Последняя строка таблицы называется оценочной строкой, а её элементы a0j оценками. Первый элемент a00 оценочной строки равен значению целевой функции Z для начального опорного плана
.
Это значение может быть получено как результат скалярного умножения вектора – столбца “сj “ на вектор – столбец свободных членов “ai0” :
Z( 
0) = a00 = 0∙220 + 0∙140 + 0∙100 = 0.
Остальные значения a0к оценочной строки получаются в результате скалярного умножения вектора – столбца “сj “ на вектор – столбец коэффициентов при переменной хк с последующим вычитанием соответствующего элемента ск верхней строки:
a01 = 0∙7 + 0∙2 +0∙5 – 2 = -2;
a02 = 0∙0 + 0∙3 +0∙1 – 1 = -1;
a03 = 0∙5 + 0∙2 +0∙1 – 1 = -1.
Оценки для базисных переменных всегда равны 0.
| cj | Базис xj | ai0 | 2 | 1 | 1 | 0 | 0 | 0 |
|
| x1 | x2 | x3 | x4 | x5 | x6 | ||||
| 0 0 0 | x4 x5 x6 | 220 140 100 | 7
 2
5
| 0 3 1 | 5 2 1 | 1 0 0 | 0 1 0 | 0 0 1 | 220/7 140/2 100/5 min |
| Z | 0 | -2 | -1 | -1 | 0 | 0 | 0 | ||
| 0 0 2 | x4 x5 x1 | 80 100 20 | 0 0 1 | -7/5
13/5
1/5
| 18/5 8/5 1/5 | 1 0 0 | 0 1 0 | -7/5 -2/5 1/5 |
 min
|
| Z | 40 | 0 | -3/5 | -3/5 | 0 | 0 | 2/5 | ||
| 0 1 2 | x4 x2 x1 | 1740/13 500/13 160/13 | 0 0 1 | 0 1 0 | 
58/13
8/13
1/13
| 1 0 0 | 7/13 5/13 -1/13 | -21/13 -2/13 3/13 |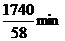 
500/8
160
|
| Z | 820/13 | 0 | 0 | -3/13 | 0 | 3/13 | 4/13 | ||
| 1 1 2 | x3 x2 x1 | 30 20 10 | 0 0 1 | 0 1 0 | 1 0 0 | 13/58 -8/58 -1/58 | 7/58 18/58 -5/58 | -21/58 4/58 15/58 | |
| Z | 70 | 0 | 0 | 0 | 3/58 | 15/58 | 13/58 |
y1 y2 y3
Исходное опорное решение 
, 
не является оптимальным, в оценочной строке три отрицательные оценки (-2), (-1), (-1), ситуация соответствует пункту 4 алгоритма симплексного метода. Перейдём к новому опорному плану:
а) разрешающий столбец соответствует переменной 
, т.к. оценка (-2) ─ наименьшая отрицательная оценка оценочной строки;
б) третья строка является разрешающей, т.к. для неё 
;
в) на пересечении разрешающих столбца и строки лежит разрешающий элемент 5, при этом в базис войдёт переменная , а переменная выйдет из базиса.
Далее заполнение новой таблицы осуществляется по методу Жордана – Гаусса.
В результате первой итерации получим новое опорное решение 
, 
.
Вторая итерация приводит к решению:
, 
.
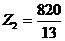После третьей итерации получаем оптимальное решение: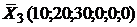 
, 
. Дальнейшее увеличение Z невозможно, т.к. все оценки оценочной строки стали неотрицательными.
Оптимальное решение исходной задачи получаем отбрасыванием из 
компонент, связанных с балансовыми переменными , , , т.е. 
, при этом значение не изменится.
Дата добавления: 2018-04-15; просмотров: 256; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!