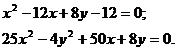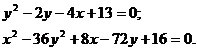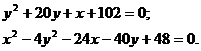Задание 1. Прямая линия на плоскости
Даны вершины треугольника ABC.
Найти:
1) длину стороны ВС;
2) уравнения сторон АВ и ВС;
3) угол В в радианах с точностью до двух знаков;
4) уравнение высоты из вершины CD и её длину;
5) уравнение медианы, проведённой из вершины А;
6) записать уравнение прямой, проходящей через вершину А параллельно стороне ВС.
Таблица 2 – Данные задания 1 « Прямая линия на плоскости»
| № | 
| 
| 
|
| 1 | (-8;-3) | (4; -12) | (8; 10) |
| 2 | (-5; 7) | (2; 2) | (11; 20) |
| 3 | (12; -1) | (0;-10) | (4; 12) |
| 4 | (-10; 9) | (2; 0) | (6; 22) |
| 5 | (0;2) | (12; -7) | (16; 15) |
| 6 | (-9; 6) | (3; -3) | (7; 19) |
| 7 | (1; 0) | (13; -9) | (17;13) |
| 8 | (-4; 10) | (8; 1) | (12; 23) |
| 9 | (2;5) | (14;-4) | (-2;16) |
| 10 | (19;3) | (11;-5) | (15; 17) |
| 11 | (-2;7) | (10;-2) | (8; 12) |
| 12 | (-6;8) | (6; -1) | (4; 13) |
| 13 | (3; 6) | (15; -3) | (13; 11) |
| 14 | (-10; 5) | (2; -4) | ( 0; 10) |
| 15 | (-4 ;12) | (8; 3) | (6; 17) |
| 16 | (-3; 10) | (9;1) | (7; 15) |
| 17 | (4; 1) | (16;-8) | (14;6) |
| 18 | (-7; 4) | (5; -5) | (3; 9) |
| 19 | (0; 3) | (12; -6) | (10; 8) |
| 20 | (-5; 9) | (7; 0) | (5; 14) |
Пример 1 Даны вершины треугольника ABC (рисунок 1):
А(-4,8), В(5,-4), С(10, 6).
Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и ВС
3) угол В в радианах с точностью до двух знаков
4) уравнение высоты СD и её длину;
5) уравнение медианы, проведённой из вершины А;
6) записать уравнение прямой, проходящей через точку С параллельно стороне АВ.
Решение:
Рисунок 1 – Треугольник АВС
1) Расстояние d между точками 
и 
определяется по формуле
(1)
Подставим в формулу (1) координаты точек А и В, получим
|
|
|
.
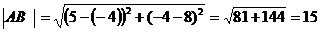2) Уравнение прямой, проходящей через две точки 
и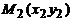 
, имеет вид
. (2)
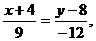
Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:
(АВ).
Для нахождения углового коэффициента 
прямой АВ разрешим полученное уравнение относительно у: 
. Отсюда 
.
Аналогично найдём уравнение прямой ВС. 
─ уравнение ВС в общем виде, или 
─ уравнение ВС с угловым коэффициентом. Угловой коэффициент прямой ВС 
.
3) Известно, что тангенс угла 
между двумя прямыми, угловые коэффициенты которых соответственно равны 
и 
, вычисляется по формуле
. (3)
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты найдены: 
; . Применяя формулу (3), получим
;
, или 
рад.
4) Найдём уравнение высоты СD и её длину.
Высота СD перпендикулярна АВ, чтобы найти угловой коэффициент высоты СD, воспользуемся условием перпендикулярности прямых. Угловой коэффициент 
будет равен 
, 
.
|
|
|
Искомая высота проходит через точку С(10,6). Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом:
. (4)
, 
(СD).
Найдём длину высоты 
.
Воспользуемся формулой расстояния от точки D 
до прямой 
:
. (5)
Длина высоты CD равна расстоянию от точки 
до прямой 
5) Обозначим основание искомой медианы через М.
По определению медианы, М делит сторону ВС пополам. Координаты точки М найдём по формуле
(6)
.
Чтобы записать уравнение медианы AM, воспользуемся формулой (2).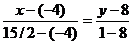 
, 
, 
, 
(АМ).
6) Найдём уравнение прямой, проходящей через точку С параллельно стороне АВ.
Обозначим искомую прямую СР. Прямые АВ и СР параллельны, по условию параллельности прямых 
. Угловой коэффициент 
, 
, т.к. искомая прямая проходит через точку С(10,6), воспользуемся уравнением (4)
, 
, 
(СP).
Задание 2. Линии второго порядка
Уравнение кривой привести к каноническому виду и построить линию.
|
|
|
Таблица 3 – Данные задания 2 «Линии второго порядка»
| Задача № | Уравнения кривых |
| Задача № | Уравнения кривых | ||
| 1 | а |
| 11 | а |
| |
| б | б | |||||
| 2 | а |
| 12 | а |
| |
| б | б | |||||
| 3 | а |
| 13 | а |
| |
| б | б | |||||
| 4 | а |
| 14 | а |
| |
| б | б | |||||
| 5 | а |
| 15 | а |
| |
| б | б | |||||
| 6 | а |
| 16 | а |
| |
| б | б | |||||
| 7 | а |
| 17 | а |
| |
| б | б | |||||
| 8 | а |
| 18 | а |
| |
| б | б | |||||
| 9 | а |
| 19 | а |
| |
| б | б | |||||
| 10 | а |
| 20 | а |
| |
| б | б |
Пример 2. Уравнение кривой привести к каноническому виду и построить линию.
1) х2 + 4у2 - 4х + 16у - 16 = 0;
2) 9x2-4y2-54x-8y+41 = 0.
Решение:
1) х2 + 4у2 - 4х + 16у - 16 = 0. Приведём данную кривую к каноническому виду и построим.
Выделим полные квадраты при х и у:
(х2-4х+4)-4+4(у2+4у+4)-16-16=0 , (х-2)2+4(у+2)2-36=0, (х-2)2+4(у+2)2=36, 
.
Получили каноническое уравнение эллипса вида
. (7)
Центр эллипса лежит в точке O/(α,β), оси параллельны осям координат ОХ и OY. Точка O/(2,-2) – центр данного эллипса. Отложим от точки O/ отрезки 
в направлениях, параллельных ОХ и OY, CС/=2 
=12 ВВ/=2 
=6 (рисунок 2).
Рисунок 2 ─ Эллипс
|
|
|
2) 9x2-4y2-54x-8y+41 = 0. Приведём данную кривую к каноническому виду и построим.
Выделим полные квадраты при х и у:
9(х2-6х+9)-81-4(у2+2у+1)+4+41 = 0 , 9(х-3)2-4(у+1)2-36 = 0,
9(х-3)2─ 4(у+1)2 = 36 , 
Получили каноническое уравнение гиперболы вида
. (8)
Центр гиперболы лежит в точке А(α,β), оси параллельны осям координат. Центр данной гиперболы лежит в точке А(3,-1), =2, =3. Построим основной прямоугольник гиперболы, откладывая от точки А отрезки =2, =3 в направлениях, параллельных основным осям координат. BB/=2∙ =4, СС/=2∙ =6. Диагонали прямоугольника будут являться асимптотами. Вершины гиперболы – точки B и B/ (рисунок 3).
Рисунок 3 ─ Гипербола
Дата добавления: 2018-04-15; просмотров: 332; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!