Знакочередующиеся ряды. Знакопеременные ряды.
Определение: Под знакочередующимсярядом понимается ряд, в котором члены попеременно то положительны, то отрицательны: u1-u2+u3-…(-1)n-1un+…, где un>0
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине u1>u2>u3>…>un>…, и предел его общего члена приn→∞ равен нулю, 
, то ряд сходится, а его сумма не превосходит первого члена: S<u1
Пример. Исследовать сходимость ряда 
Решение. Так как члены знакочередующегося ряда убывают по абсолютной величине 1> 
, и предел общего члена 
, то по признаку Лейбница ряд сходится
Пусть u1+u2+u3+…+un+…знакопеременный ряд, в котором любой его член un, может быть как положительным, так и отрицательным.
Теорема (достаточный признак сходимости знакопеременного ряда).Если ряд, составленный из абсолютных величин членов данного ряда u1+u2+u3+…+un+…, т.е. 
, сходится, то сходится и данный ряд.
Определение: Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример:Ряд 
согласно теореме абсолютно сходящийся, так как сходится ряд, составленный из абсолютных величин членов данного ряда: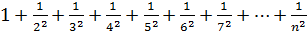 
Пример:Ряд 
условно сходящийся, так как по признаку Лейбница он сходится, т. е. удовлетворяет условиям 1> 
и 
|
|
|
А ряд 
, составленный из абсолютных величин его членов, расходится (гармонический ряд).
Дата добавления: 2018-05-01; просмотров: 291; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!