Векторное произведение векторов
Обозначение: 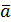 х
х 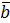 или [
или [ 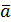 ,
, 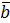 ]
]
Выражение векторного произведения через координаты
Для определения векторного произведения через координаты будем использовать таблицу векторного произведения векторов 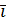 ,
, 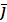 и
и 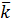 :
:
| * | 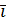
| 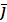
| 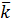
|
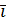
| 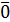
| 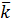
| - 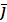
|
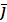
| - 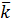
| 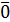
| 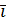
|
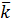
| 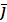
| - 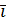
| 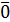
|
Теорема: Если векторы 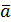 и
и 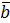 заданы своими координатами:
заданы своими координатами: 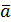 = {x1, y1, z1},
= {x1, y1, z1}, 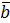 ={x2, y2, z2}, то векторное произведение вектора
={x2, y2, z2}, то векторное произведение вектора 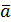 на вектор
на вектор 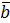 определяется формулой:
определяется формулой:
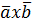 =
= 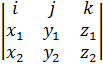 =
= 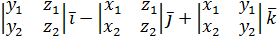 – разложение определителя третьего порядка по элементам первой строки.
– разложение определителя третьего порядка по элементам первой строки.
5. Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 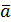 ,
, 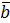 ,
, 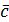 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 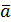 на векторное произведение векторов
на векторное произведение векторов 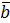 х
х 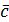 , т.е.
, т.е. 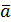 (
( 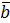 х
х 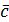 ).
).
ТЕМА 3. Элементы аналитической геометрии на плоскости и в пространстве
Лекция № 4.
Тема:Прямая линия на плоскости
1. Виды уравнений прямой на плоскости.
Общее уравнение прямой
Имеет вид Ax+By+C=0, где А и В – одновременно не равны 0
Определение.Уравнением линии называется такое уравнение, которому удовлетворяют координаты всех точек, лежащих на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на линии
Обозначение: В общем виде F(x, y)=0 или y=f(x) (если возможно),
где F(x, y), f(x) – некоторые функции
1. Уравнение прямой с угловым коэффициентом
имеет вид y=kx+b,где k-угловой коэффициент прямой, равный k=tgα
Тема:Плоскость и прямая в пространстве
|
|
|
1. Виды уравнений плоскости в пространстве.
Пусть точка Mo(x0,y0,z0) лежит на плоскости и вектор 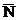 (A,B,C) перпендикулярен к плоскости (рис.1)
(A,B,C) перпендикулярен к плоскости (рис.1)
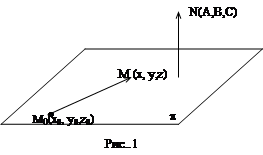 |
Возьмём на плоскости p любую точку M(x,y,z), образуем вектор 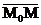 и используем условие перпендикулярности двух векторов
и используем условие перпендикулярности двух векторов 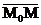 и
и 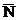 .
.
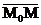 ^
^ 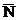 Þ (
Þ ( 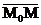 ,
, 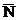 ) = 0
) = 0
Запишем уравнение данное уравнение в координатной форме.
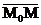 (x0-x, y0-y, z-z0),
(x0-x, y0-y, z-z0), 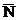 (A, B, C)
(A, B, C)
( 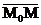 ,
, 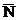 ) = A(x-x0) + B(y0-y) + C(z-z0)
) = A(x-x0) + B(y0-y) + C(z-z0)
Преобразуя последнее выражение, получим Ax+By+Cz+D=0, где
D=-Ax0-By0-Cz0
Уравнение Ax+By+Cz+D=0 называется общим уравнением плоскости в пространстве.
ТЕМА 4. Введение в математический анализ.
Тема 1:Теория пределов
Лекция № 5.Функции и их свойства. Предел последовательности и функции.
План:
1. Функции и их свойства.
2. Числовая последовательность.
3. Предел функции в точке.
4. Предел функции на бесконечности.
5. Основные теоремы о пределах.
6. Замечательные пределы.
Функции и их свойства.
Определение: Пусть заданы некоторые числовые множества X, Y.
Если каждому элементу x множества X ставиться в соответствие определенный элемент y множества Y, то говорят, что на множестве X задана функция y=f(x).
|
|
|
Переменная x называется независимой переменной или аргументом, y – зависимой или функцией
Множество X – область допустимых значений независимой переменной x, множество Y- множество значений функции.
Определение: Графиком функции y=f(x) называется множество всех точек плоскости Oxy, для каждой из которых x является значением аргумента, а y соответствующим значением функции.
Способы задания функции:
1. Аналитический способ. При этом способе указывается формула, связывающая зависимую переменную величину с независимой переменной величиной.
2. Табличный способ. При этом способе выписываются в определенном порядке значения аргумента x1, x2, x3…xn и соответствующие значения функции y1, y2, y3…yn
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
3. Графический способ. Этот способ удобен, когда задать функцию аналитически довольно трудно. Этот способ состоит в изображении графика функции – т. е. множества точек (x, y) плоскости, абсциссы которых есть значения аргумента x, ординаты – соответствующие им значения функции y=f(x).
4. Словесный способ. Функция описывается правилом составления.
Основные свойства функции:
1. Четность и нечетность функции.
|
|
|
Определение: Функция y=f(x) называется четной, если при всех значениях x из области определения этой функции выполняется условие f(-x)=f(x).
Определение: Функция y=f(x) называется нечетной, если при всех значениях x из области определения этой функции выполняется условие f(-x)=-f(x).
Замечание: Если функция не является не четной и не нечетной, то функция является функцией общего вида.
2. Монотонность функции.
Определение: Функция y=f(x) называется монотонно возрастающей (возрастающей) на множестве X, если большему значению аргумента из этого промежутка соответствует большее значение функции, т. е. для x1, x2ϵX и x2>x1, следовательно, f(x2)>f(x1)
Определение: Функция y=f(x) называется монотонно убывающей (убывающей) на множестве X, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т. е. для x1, x2ϵX и x2>x1, следовательно, f(x2)<f(x1)
Функции возрастающие и убывающие называются монотонными функциями.
3. Ограниченность функции.
Определение: Функция y=f(x) называется ограниченной на промежутке X, если существует такое положительное число М>0, что |f(x)|≤M для любого xϵM. В противном случае, функция называется неограниченной.
4. Периодичностьфункции.
|
|
|
Определение: Функция y=f(x) называется периодической, если существует число Т≠0, такое, что при любых x из области определения функции выполняется условие f(x+T)=f(x). Число Т называется периодом функции.
Числовая последовательность.
Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность
x1, х2, …, хn= {xn}
Общий элемент последовательности является функцией от n, т.е.xn = f(n)
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Пример. {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …
Определение. Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство: 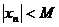
т.е. все члены последовательности принадлежат промежутку (-М; M).
Определение. Последовательность {xn}называется ограниченной сверху, если для любого n существует такое число М, что xn£M.
Определение. Последовательность {xn}называется ограниченной снизу, если для любого n существует такое число М, что xn³M
Определение.Числоа называется пределом последовательности {xn}, если для любого положительного e>0 существует такой номер N, что для всех n>N выполняется условие: 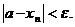
Обозначение:limxn = a.
В этом случае говорят, что последовательность {xn}сходится к а при n®¥.
Теорема. Последовательность не может иметь более одного предела.
Определение.
1) Если xn+1>xn для всех n, то последовательность возрастающая
2) Если xn+1³xn для всех n, то последовательность неубывающая.
3) Если xn+1<xn для всех n, то последовательность убывающая.
4)Если xn+1£xn для всех n, то последовательность невозрастающая
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример. {xn} = 1/n – убывающая и ограниченная, {xn} = n – возрастающая и неограниченная.
Предел функции в точке.
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
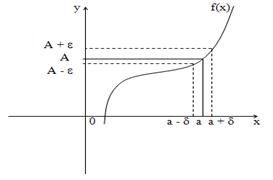
Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число d>0, что для всех х таких, что
0 <ïx - aï<d верно неравенствоïf(x) - Aï<e.
Обозначение: 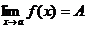
Определение.Если f(x) ®A1 при х ® а только при x<a, то 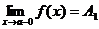 - называется пределом функции f(x) в точке х = а слева, а если f(x) ®A2 при х ® а только при x>a, то
- называется пределом функции f(x) в точке х = а слева, а если f(x) ®A2 при х ® а только при x>a, то 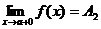 называется пределом функции f(x) в точке х = а справа.
называется пределом функции f(x) в точке х = а справа.
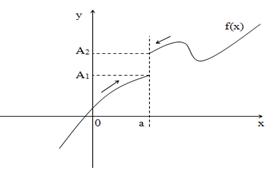
Данное определение справедливо для функции f(x), которая не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А1 и А2 называются односторонними пределами функции f(x) в точке х = а.
Дата добавления: 2018-05-01; просмотров: 267; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
