Линейный регрессионный анализ

⇐ ПредыдущаяСтр 9 из 14Следующая ⇒

В экологических исследованиях, и особенно в экспериментальных данных, обычно используется регрессионный анализ, который тесно связан с корреляционным анализом и является его логическим продолжением, углубляя представления о корреляционной связи в следующих важных направлениях. Во-первых, приемы регрессионного анализа позволяют выявить и графически отобразить зависимость изменения одного признака от изменения другого (регрессию у по х обозначают у/х, и регрессию х по у соответственно х/у). Во-вторых, на основе составления и решения уравнений регрессии становится возможным выравнивание эмпирических линий регрессий, т.е. моделирование наблюдений зависимости путем подбора соответствующей функции, график которой и представляет собой теоретическую линию регрессии. В-третьих, если подобранная функция не только формально описывает связь в интервале интерполяции эмпирических данных, но отражает биологическую сущность явления, то открывается перспектива прогнозирования значений признака в зоне экстраполяции, т.е. за пределами ряда фактически сделанных наблюдений. Итак, под регрессией подразумевается зависимость изменений одного признака от изменений другого или нескольких признаков (множественная регрессия). В соответствии с этим регрессия, подобно корреляции, может быть парной (простой) или множественной, а в зависимости от формы связи – линейной или нелинейной. В отличие от корреляционного анализа, требующего достаточно большого объема выборки, анализ регрессии возможен и при наличии всего нескольких пар сопряженных наблюдений, однако его имеет смысл проводить лишь при обнаружении достоверных и достаточно сильных (порядка r≥0,7) связей между признаками. Начинать регрессионный анализ целесообразно с построения эмпирических линий регрессии, по которым можно визуально определить характер связи (линейная, нелинейная, асимптотическая и т.п.).

Прежде чем переходить к множественному регрессионному анализу, уясним основные статистики и формулы расчета параметров для простой линии регрессии (у/х). Точки эмпирических линий регрессии вычисляются либо как взвешенные средние арифметические по строкам и столбцам корреляционной решетки:

, j = 1÷k (4.16)

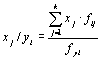, i = 1÷m (4.17)

либо по прямым наблюдениям соответствующих у, х признаков для заранее определенных равномерных интервалов по х как среднеарифметические 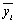, где i= 1,2,…, n_i – номер интервала по х, а по у как – среднеарифметические для интервала по у.

Эмпирическая линия регрессии

Для примера построения эмпирической линии регрессии рассмотрим зависимость между длиной и шириной листа у Melampyrum polonicum (Beauv.) Soo. Корреляционная решетка и рассчитанные точки эмпирических линий регрессии у/х и х/у даны в табл. 4.3, а сами эмпирические линии регрессии нанесены на график (рис. 4.1).

Таблица 4.3.– Корреляция между длиной (у) и шириной (х) листа(в мм)уMelampyrum polonicum (Beauv.) Soo и точки эмпирических линий регрессии у/х и х/у

х у	1	4	7	10	13	16	f_y	x/y
19,5 29,5 39,5 49,5 59,5 69,5	1	2 9 3	4 10 7 1	1 6 3	6 1	1 1	3 13 14 19 5 2	3,0 4,9 6,6 9,8 10,6 14,5
f_x y/x	1 19,5	14 30,2	22 41,8	10 51,5	7 52,4	2 64,5	п=56

Графическое изображение эмпирических линий регрессии надо считать обязательным, т.к. по их внешнему виду можно сделать некоторое предварительное заключение о характере связи. При полном отсутствии связи эмпирические линии регрессии, пересекаясь под прямым углом, располагаются параллельно осям графика. Чем сильнее связь, тем меньше угол между линиями: при полной связи они параллельны друг другу.

Рисунок 4.1 – Эмпирические линии регрессии длины (у) и ширины (х) листа
Melampyrum polonicum 1 – регрессия у/х, 2 – регрессия х/у

Направление эмпирических линий регрессии говорит о знаке связи, а их конфигурация ориентировочно указывает на степень линейной связи (при этом надо оценивать основную тенденцию хода кривых на графике, мысленно сглаживая их изломы). Обладая определенными навыками, исследователь по форме эмпирической линии регрессии может достаточно уверенно судить о том, какая теоретическая функция окажется пригодной для ее выравнивания.

Из рассмотренного примера (рис. 4.1) видно, что связь между длиной и шириной листа Melampyrum polonicum положительна (с увеличением значений одного признака возрастают и значения другого) и достаточно сильна (угол между линиями невелик). Форма кривых наводит на мысль о некоторой нелинейности связи, однако для начала целесообразно попытаться описать наблюдаемую регрессию более простыми линейными методами.

Линейная регрессия

В общем виде суть простого регрессионного анализа можно представить в следующем виде.

Рассмотрим ситуацию, когда две переменные связаны линейным соотношением. Пусть Y – зависимая, X – независимая переменные.

Предположим, что имеется выборка парных наблюдений (х₁, у₁), (х₂, у₂),…, (х_п, у_п)из некоторой популяции W. Первый способ состоит в том, что значения X фиксируются, т.е. X=х₁,…, X=х_п, так, что дляX=х_iмы имеем подпопуляцию W_i из W, содержащую все индивидуумы, для которых X=х_i_,i=1,…, п. Из Wi случайным образом выбирается индивидуум, у которого измеряется Y=у_i_,i=1,…,п. При таком подходе толькоYявляется случайной величиной.

При втором методе получения выборки мы случайным образом отбираем п индивидов из W и у каждого из них измеряем как переменные X, так и Y. Здесь случайными являются обе величины X и Y. Преимущество этого метода получения выборки заключается в том, что мы можем сделать статистические выводы относительно коэффициента корреляции между X и Y, в то время как при первом методе этого сделать нельзя.

Независимо от способа получения выборки имеются два предварительных шага для определения существования и степени линейной зависимости между X и Y. Первый шаг заключается в графическом отображении точек (х₁,у₁),…,(х_п,у_п)на плоскость XY. Такой график называется диаграммой рассеяния. Анализируя ее, мы можем эмпирически решить, допустимо ли предположение о линейной зависимости между X иY.

Вторым шагом является вычисление выборочного коэффициента корреляции

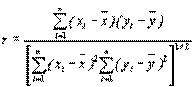(4.18)

Если абсолютная величина коэффициента корреляции велика, это обоснованно указывает на сильную линейную зависимость между переменными.

В современных статистических программах для ПЭВМ одновременно с вычислением коэффициента корреляции можно построить и диаграммы рассеяния.

Если предполагается линейная зависимость между X и Y, то теоретическая модель задается уравнениями

Y_i=b₀+ b₁x_i+e_i i=1,…,n (4.19)

и называется моделью простой линейной регрессииYпоX.Величиныb₀иb₁являются неизвестными параметрами, а е₁,е₂,…,е_псуть некоррелированные ошибки случайной переменной со средним 0 и неизвестной дисперсиейs², т.е.Е(е_i)=0 иV(е_i)= s², i=1,…,n.

Наилучшие оценки значений b₀ и b₁ для b₀ и b₁ получаются минимизацией соответственно по b₀ и b₁ суммы квадратов отклонений

. (4.20)

Эти оценки называются оценками наименьших квадратов и даются формулами:

(4.21)

. (4.22)

Отметим, что S – естьмера ошибки, возникающей при аппроксимации выборки прямой. Оценки b₀ и b₁ минимизируют ошибку.

Оценкой уравнения регрессии (прямой наименьших квадратов) будет

, (4.23)

так что оценка значения Y при X=x_i есть . Разница между наблюдаемым и отклоненным значением Y при X=x_i называется отклонением или остатком . Прямая наименьших квадратов доставляет минимум сумме квадратов отклонений.

Во многих пакетах статистических программ вычисляются оценки b₀ и b₁ наименьших квадратов. Они на выходе обычно называются коэффициентом регрессии b₁ и свободным членом b₀. Соотношение между теоретической регрессионной прямой, прямой наименьших квадратов и точками выборки изображены на рис. 4.2.

Чтобы сделать статистические выводы о и , сначала необходимо оценить дисперсию ϭ², а затем описать распределение ошибки случайной переменной eⁱ, i=1,…,n. Согласно теории общей линейной модели обычная несмещенная оценка для ϭ² определяется через дисперсию оценки

(4.24)

Рисунок 4.2–Теоретическая регрессионная прямая наименьших квадратов с указанным i-м отклонением . Прямая наименьших квадратов доставляет минимум S. Пунктирная линия – прямая наименьших квадратов , сплошная линия – неизвестная теоретическая прямая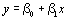

Положительный квадратный корень из этой величины называют стандартной ошибкой оценки. Дисперсию оценки можно также найти из таблицы дисперсионного анализа (табл. 4.4).

Величина s² идентична MS_R – среднему квадрату отклонения (остатка) от регрессии. Остаточная сумма квадратов SS_R и остаточное число степеней свободы n_R являются соответственно числителем и знаменателем в формуле (4.24).

Таблица 4.4.– Таблица дисперсионного анализа для простой линейной регрессии

Источник дисперсии	Сумма квадратов	Степени свободы	Средний квадрат	F-отношение
Регрессия Отклонение от регрессии Полная			MS_D=SS_D

Обусловленная регрессией сумма квадратов SS_D получила такое название потому, что ее можно записать как функцию оцененного коэффициента регрессии b₁, именно

. (4.25)

Итак, чем больше коэффициент регрессии, тем больше сумма квадратов, «обусловленная регрессией».

F-отношение может быть использовано для проверки гипотез, если ошибки е₁, е₂,…,е_п предполагаются нормально распределенными. В этом случае моделью простой линейной регрессии будет

, (4.26)

где е₁, е₂,…, е_п – независимые случайные ошибки, распределенные по нормальному закону.

Для проверки гипотезы о том, что простая линейная регрессия Y по X отсутствует, т.е. гипотезы H₀: b₁=0 против альтернативы H₁: b₁¹0, мы используем F-отношение из таблицы дисперсионного анализа

. (4.27)

Если верна гипотеза H₀, то F₀ имеет F-распределение с n_D=1 и n_R=п-2 степенями свободы на уровне значимости a=0,05 – общепринятого для биологии, причем F₀ < F_st.

В качестве примера приведем расчет линейной регрессии для вида M. polonicum, который можно провести с помощью микрокалькулятора. Определение линейной регрессии совпадает с определением линейной корреляции: равномерным изменениям одного признака соответствуют равномерные в среднем изменения другого признака. Указанием на линейность служит возможность проведения на графике от руки прямой линии таким образом, чтобы точки эмпирической линии регрессии располагались по обе стороны от прямой и по возможности ближе к ней.

Уравнением линейной регрессии служит уравнение прямой линии: y=a+bx, где у – значение зависимой переменной (признака); х – значение независимой переменной (признака или фактора, влияющего на первый признак); а – начальное значение у при х=0; b – угловой коэффициент (тангенс угла наклона линии регрессии к оси абсцисс, отражающий пропорциональную зависимость у от х).

Задача состоит в нахождении неизвестных параметров а и b. Для этого составляется и решается система стольких, так называемых нормальных уравнений, сколько неизвестных требуется определить.

В случае линейной регрессии у/х система состоит из двух уравнений и выглядит следующим образом:

(4.28)

где у – точки эмпирической линии регрессии у/х; п – число пар сопряженных наблюдений; х – значение признака, а и b – коэффициенты.

Необходимые для подстановки в нормальные уравнения суммы ) удобно рассчитывать в табличной форме. Применительно к нашему примеру регрессии длины листа M.polonicumна его ширину (табл. 4.3) соответствующие расчеты выполнены в левой части табл. 4.5, причем требуемые суммы указаны в нижней ее строке. Подставляем эти суммы в систему нормальных уравнений:

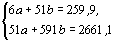
и решаем ее обычным алгебраическим путем. Для этого, разделив первое уравнение на 6, а второе на 51, освободимся от коэффициентов при неизвестном а:

и после вычитания первого уравнения из второго получим 3,09b=8,86, откуда следует, что b=2,87. Подставив значение b=2,87 в любое из ранее полученных уравнений, находим, что а=18,92. Теперь можно записать искомое уравнение регрессии: у=18,92+2,87х.

Таблица 4.5.– Выравнивание эмпирической линии регрессии длины листа (у) на его ширину (х) у Melampyrum polonicum (Beauv.) уравнением прямой линии (y’)

Расчеты для определения параметров уравнения				Построение теоретической линии регрессии		Расчет критерия χ²
х	у	х²	ху	bx	a+bx=y’	y-y’	(y-y’)²
1 4 7 10 13 16	19,5 30,2 41,8 51,5 52,4 64,5	1 16 49 100 169 256	19,5 120,8 292,6 515,0 681,2 1032	2,87 11,48 20,09 28,7 37,31 45,92	21,79 30,4 39,01 47,62 56,23 64,84	-2,29 -0,2 2,79 3,88 -3,83 -0,34	5,2441 0,04 7,7841 15,0544 14,6689 0,1156	0,2407 0,0013 0,1995 0,3161 0,2609 0,0018
51	259,9	591	2661,1	–	259,89	0,01	42,9071	1,0203

Посредством обратного вычисления, последовательно подставляя в найденное уравнение значения х=1, х=4,х=7 и т.д. (табл. 4.4.), рассчитываем точки (y’) теоретической линии регрессии. Теоретическую линию регрессии для ее визуального сравнения с эмпирической полезно нанести на график (рис. 4.3а), а степень их совпадения можно проверить посредством расчета критерия χ². Полученное значение χ²=1,0203 далеко не достигает стандартных значений этого критерия, составляющих при ν=п-1=5 χ²₀₅= 11,1 и χ²₀₁= 15,1, указывая на достаточно хорошее соответствие теоретической линии регрессии эмпирическому ряду.

Ошибка уравнения регрессии рассчитывается по формуле

(4.29)

где n – число точек линии регрессии, k – число коэффициентов в уравнении регрессии, включая свободный член.

В нашем примере ∑(y-y’)²=42,9071; n=6 и k=2, поэтому

Это средний показатель точности, с которым «работает» выведенное нами уравнение регрессии.

Рисунок 4.3 – Выравнивание эмпирической линии регрессии у/х (1) уравнением
прямой линии (2) по данным табл. 4.5 (а), уравнением параболы второй
степени (2) по данным табл. 4.9 (б) и уравнением параболы третьей
степени (2) по данным табл. 4.10 (в)

По аналогии с вышеизложенным рассчитывается и вторая теоретическая линия регрессии (х/у), для чего в системе нормальных уравнений признаки х и у следует поменять местами:

(4.30)

Исходя из данных табл. 4.5, можно выполнить необходимые расчеты. Мы приводим лишь итоговое уравнение теоретической линии регрессии х/у: х=-1,56+0,22у.

Удовлетворительно интерполируя эмпирические данные, уравнение прямой линии в нашем примере не в состоянии, однако, обеспечить экстраполяцию за пределы эмпирического ряда наблюдений. В этом легко убедиться, если, например, в уравнении у=18,92+2,87х придать ширине листа (х) нулевое значение: длина листа (у) при этом окажется равной 18,92 мм, что лишено биологического смысла. Таким образом, линейная функция не отражает полностью биологическую сущность связи между длиной и шириной листа. Если нас не удовлетворяет формальная интерполяция, мы должны продолжить поиск и найти такую функцию, которая наряду с интерполяцией позволяла бы проводить экстраполяцию (и обеспечить нулевое значение длины листа при нулевой его ширине).

Угловой коэффициент (b) в уравнении линейной регрессии, отражающий пропорциональную зависимость между признаками, называется коэффициентом регрессии (R). Для признаков длины и ширины листа у M.polonicum мы получили в предыдущем разделе два уравнения регрессии (у/х и х/у), из которых следует, что R_y_/_x=2,87, а R_x_/_y= 0,22.

Биологический смысл коэффициентов регрессии состоит в том, что они представляют собой меру изменения одного признака от определенного изменения другого. В нашем примере R_y_/_x=2,87 говорит о том, что с увеличением ширины листа (х) на 1мм (принятая точность измерения) его длина (у) увеличивается в среднем на 2,87 мм. Второй коэффициент (R_x_/_y= 0,22) свидетельствует о том, что при увеличении длины листа (у) на 1 мм его ширина (х) возрастает в среднем на 0,22 мм.

Коэффициенты регрессии могут быть вычислены и без составления уравнения регрессии. Один из способов основан на предварительном вычислении тех сумм, которые применительно к регрессии у/х указаны в нижней строке табл. 4.5 (для определения величины R_x_/_y нужно составить аналогичную таблицу, поменяв местами х и у). Соответствующие формулы дают следующие результаты:

(4.31)

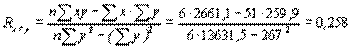(4.32)

Значение первого коэффициента полностью совпадает с ранее рассчитанным, а небольшое отклонение второго (против величины 0,22, полученной ранее) объясняется потерей десятичных знаков при промежуточных вычислениях. Мы привели основные уравнения для расчета коэффициентов регрессии на микрокалькуляторах для того, чтобы была понятна суть этого метода анализа данных. Естественно, что в настоящее время имеются статистические пакеты, используя которые, можно рассчитать все параметры с оценкой достоверности. Но мы считаем, что для понятия смысла регрессионного анализа полезно знать формулы расчетов.

Другой способ определения коэффициентов регрессии может быть использован тогда, когда предварительно проводился корреляционный анализ и известно значение коэффициента корреляции (r) между признаками, а также их средние квадратичные отклонения:

, (4.33)

где σ_у и σ_х – «полные» сигмы, взятые с учетом классового интервала.

Эти формулы наглядно показывают тесную связь регрессионного анализа с корреляционным: перемножение их левых и правых частей приводит к выражению:

, (4.34)

из которого следует вывод, что коэффициент корреляции есть среднее геометрическое из двух коэффициентов регрессии. Сказанное соответствует биологическому смыслу показателей: коэффициент корреляции является относительной величиной, показывающей обоюдную степень связи между признаками, а коэффициенты регрессии – величины, конкретизирующие зависимость каждого из признаков от другого.

В примере с M.polonicum коэффициент корреляцииr=0,799, а средние квадратичные отклонения признаков σ_у=11,8 мм, σ_х=3,3 мм. Отсюда

и, как видим, результат практически тождествен тому, который ранее был получен другими способами.

Как всякая выборочная величина, коэффициент регрессии имеет свою ошибку репрезентативности и с ее помощью может быть оценена его достоверность. Покажем это применительно к коэффициенту регрессии R_y_/_x в нашем примере. Ошибка показателя вычисляется следующим образом:

== 0,29 (4.35)

Далее можно использовать критерий t:

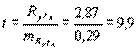(4.36)

и при ν=п-2=56-2=54 (здесь п – объем выборки по табл. 4.3.) полученное значение t высоко достоверно, т.к. значительно превышает табличное t₀₁=2,68. Это свидетельствует о достоверности рассчитанного коэффициента регрессии.

Дата добавления: 2018-04-15; просмотров: 1243; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!