Словесные и математические модели
Специалисты по системному анализу считают построение «словесной» модели важным этапом, на котором объединяется все, что связано с решаемой проблемой, с целью выделения той части системы, которую, с их точки зрения, необходимо исследовать. Часто ученые, занимающихся одной и той же проблемой, не соглашаются с описанием своих коллег, предложенным для данной экологической системы. Поэтому есть все основания потратить определенное время на то, чтобы найти описание, удовлетворяющее всех заинтересованных исследователей, даже если в нем будут некоторые пробелы, отражающие те моменты, по которым не удалось прийти к общему мнению. Такое описание может во многом помочь на стадиях постановки задачи и ограничения ее степени сложности и установления иерархии целей и задач исследования. В такой роли «словесная» модель может принести неоценимую пользу.
Сила математики заключается в ее способности выражать идеи и особенно сложные связи с помощью символьной логики, сохраняя в то же время простоту и рациональность выражения. Знание математической системы обозначений покоится на выражении связей через символьную логику, и это выражение является «формальным» в том смысле, что из него можно формальными способами получить некоторые предсказания. Не будь этой способности предсказывать результаты изменений одного или более элементов связей, мы бы не моглисчитать эти выражения научной, а не просто литературной записью. Поэтому использование математических обозначений в моделировании сложных систем является попыткой дать содержательную символику, которая упрощает, но не слишком искажает основные взаимосвязи.
|
|
|
Различные математические правила манипулирования со связями системы позволяют нам делать предсказания относительно тех изменений, которые могут произойти в экологических системах, когда изменяются их составляющие. Такие предсказания в свою очередь позволяют сравнивать модельные системы с теми реальными объектами, которые они должны представлять, и проверять тем самым адекватность модели наблюдениям и экспериментальным данным. Манипуляции с самой модельной системой могут подсказать, какие реальные эксперименты необходимо поставить для проверки адекватности модели.
Существуют различия между понятиями «модель» и «имитация». «Имитацией» считают максимально подробное математическое описание с какой-то практической целью, а под термином «модель» понимают описание общих идей, содержащее как можно меньше деталей. Мы будем считать моделью любое формальное описание связей между определенными символами, эти модели мы будем применять для того, чтобы имитировать реакцию экологической системы в ответ на различные воздействия. Таким образом, в прикладном системном анализе мы будем стремиться к слиянию понятий «модель» и «имитация».
|
|
|
В общем случае математические модели классифицируют на детерминистские и стохастические, хотя в последнее время в связи с бурным развитием вычислительной техники и различных приложений практически все модели являются смешанными и еще с элементами имитации.
Если предыдущее состояние системы однозначно определяет последующее состояние, то система или модель называется детерминистской. В качестве примера можно привести модели, описанные с помощью дифференциальных уравнений. Если, зная состояние системы в данный момент времени, можно лишь указать вероятности наступления того или иного состояния в следующий момент времени, то система называется вероятностной или стохастической. Для описания и исследования таких систем применяется математический аппарат теории случайных процессов.
Существует деление математических моделей и по способу описания динамики моделируемого объекта. Если и время, и состояние моделируемого объекта описываются на бесконечных непрерывных множествах (например время и численность популяции), то называют такую модель непрерывно-непрерывной (системы дифференциальных уравнений). Если время принимает только целые положительные значения, а состояние – на непрерывных множествах, то такая модель называется дискретно-непрерывной (уравнения в конечных разностях). Если и время, и состояние моделируемой системы описываются на дискретных множествах, то такую модель называют дискретно-дискретной. Примером может служить оценка численности популяции в баллах (мало, немного, много особей и т.д.). В этом случае применяется математический аппарат теории конечных автоматов, сюда можно отнести матричные модели и т.п.
|
|
|
Детерминистские модели
Одной из простейших моделей роста популяции организмов является модель, заданная дифференциальным уравнением:
, (3.1)
где y – плотность популяции в момент t, r – константа. Один из примеров биологического процесса, который может быть представлен подобной моделью, – это рост бактериальной культуры до того, как начнет истощаться среда. Здесь скорость роста в любой момент времени равна постоянной доле от плотности популяции в этот момент. Выражая эту связь в такой форме, мы можем, решая уравнение (3.1), получить выражение для плотности популяции в любой момент времени:
|
|
|
, (3.2)
где y– плотность популяции в момент t, y0 – плотность в момент t=0, r – константа, а e – основание натурального логарифма.
Эта простая экспоненциальная модель имеет довольно ограниченное применение, поскольку плотность популяции организмов будет по мере исчерпания питательных веществ достигать некоторого стационарного значения. Альтернативной моделью, обладающей данным свойством, является дифференциальное уравнение:
, (3.3)
где y – вновь плотность популяции в момент времени t, a и b – константы. Аналогично, решая дифференциальное уравнение, получим:
. (3.4)
Эта логистическая модель достаточно хорошо описывает рост бактериальных популяций в условиях, когда запасы питательных веществ ограничены. Сначала рост популяции носит экспоненциальный характер, а затем, по мере исчерпания ресурсов, постепенно замедляется, пока плотность популяции не достигнет постоянного уровня или асимптоты. Более того, предсказать, что этот постоянный уровень равенa/b, мы можем при помощи простых алгебраических манипуляций с исходной моделью, т.е. посредством логической дедукции в рамках символьной логики математического выражения нашей модели. Иными словами, выражая модель в абстрактных математических терминах, мы сразу же приобретаем возможность получения из модели дальнейшей информации. Обе модели являются детерминистскими в том смысле, что при заданных значениях констант плотность популяции в данный момент времени t всегда одна и та же: величина Y однозначно определяется значением t.
Стохастические модели
Модели, задаваемые дифференциальными уравнениями, были разработаны вначале в приложениях математики к физике и, естественно, что в поисках моделей для экологии прежде всего стоит посмотреть, нельзя ли использовать то, что было развито в других областях.
Можно строить наши модели совершенно иным способом, положив в их основу изменчивость живых организмов, тогда это будут вероятностные или стохастические модели. В подобных моделях используется совсем иная область математики, развившаяся позже, чем дифференциальное исчисление и дифференциальные уравнения. Один простой пример такой модели, соответствующий детерминистской модели экспоненциального роста, задается уравнением:
, (3.5)
где y– плотность популяции в момент времени t, a – константа, b(t) –случайная переменная с нулевым средним. Это значит, что величина b(t) меняется, принимая значения из некоторого случайного распределения так, что между флуктуациями в последовательные моменты нет никакой корреляции. Легко видеть, что если основой для имитации служит стохастическая модель, то результаты имитации будут различаться, даже если константы и начальные условия одинаковы. Эту вариабельность обеспечивают вероятностные элементы модели; назначение таких моделей именно в том и состоит, чтобы отразить изменчивость, характерную для живых организмов и экологических систем. Что же касается постановки реального эксперимента, то обычно бывает необходимо провести целую серию имитаций, с тем чтобы определить, как система реагирует на различные воздействия.
Мы коротко рассмотрели два типа моделей:
1) детерминистские модели, в которых предсказываемые значения могут быть точно вычислены;
2) стохастические модели, в которых предсказываемые значения зависят от распределения вероятностей.
Это различие важно иметь в виду, и далее мы рассмотрим, как с помощью распределения вероятностей осуществляется подгонка моделей, т.е выбор таких значений параметров, при которых предсказанные величины достаточно близки к результатам наблюдений. Оценка таких параметров требует применения статистических методов, которые опираются на теорию вероятностей. И здесь следует различать популяцию и выборку. Под популяцией понимается такое множество индивидов, свойства которых мы хотим исследовать. Эти индивиды могут быть организмами, экосистемами или даже любой характеристикой организмов или экосистем.
Выборка – это любое конечное множество индивидов, извлеченное из популяции, при этом считается, что выборка делается таким образом, что вычисленные по ней величины являются показательными (репрезентативными) для всей популяции и могут поэтому рассматриваться как оценки соответствующих величин для этой популяции. Методы, которыми проводятся выборки, мы рассматривать не будем.
Величины, характеризующие популяцию в целом, определим как параметры либо как константы или коэффициенты в уравнениях модели. Необходимо все время помнить о разнице между параметрами и выборочными оценками.
Уравнения, задающие модель, будут содержать два типа переменных. По крайней мере, одна из переменных будет зависимой в том смысле, что она меняется при изменении других переменных. В рассмотренных выше примерах такой величиной является плотность популяции y. Другие переменные считаются независимыми, например t.
Определим подгонку моделей как выбор таких значений параметров, при которых предсказанные значения величин достаточно близки к наблюдаемым. В действительности, вероятность того, что параметры отвечают данным наблюдений, мы будем рассматривать как математическую функцию этих параметров и определим ее как функцию правдоподобия. Эта функция является мерой соответствия между моделью и данными, а те значения параметров, для которых правдоподобие максимально, называются оценками максимального правдоподобия.
Кроме того, модели подразделяются еще на две категории, а именно аналитические и имитационные.
Аналитические модели– это те, в которых для определения значений предсказываемых величин получаются выражения в явном виде, сюда относятся регрессионные и многомерные модели, модели планирования эксперимента и стандартные теоретические статистические распределения.
Имитационные модели – это те, которые могут быть описаны с помощью набора определенных математических операций, таких как решение дифференциальных уравнений, повторное применение переходной матрицы или использование случайных чисел, различные регрессии. Преимущество имитационных моделей состоит в том, что их легче построить не математику, но подогнать их под данные наблюдений обычно труднее, чем аналитические модели.
Динамические модели
К динамическим моделям можно отнести все модели, где рассматриваются различные параметры биосистем в динамике от времени или другой независимой величины.
Всякое практическое использование динамических моделей зависит от способности современных ЭВМ решать большое число (сотни) уравнений за короткие промежутки времени. Эти уравнения являются более или менее сложными математическими описаниями того, как функционирует имитируемая система, и даются они в форме выражений для уровней различных типов, темп изменения которых регулируется управляющими функциями. Уравнения для уровней описывают накопления в системе таких величин, как масса, численность организмов или количество энергии, а уравнения для темпов управляют изменением этих уровней во времени. Управляющие функции отражают правила, явные или неявные, которые регулируют функционирование системы. Математические модели системы могут отображать ее лишь с той степенью точности, с какой уравнения, описывающие свойства компонентов модели, отображают свойства компонентов реальной системы. Популярность динамических моделей обусловлена большой гибкостью методов, применяемых для описания динамики систем, которая включает нелинейные реакции компонентов на регулирующие переменные, а также положительные или отрицательные обратные связи. Такая гибкость имеет и свои недостатки. Например, невозможно учесть уравнения для всех компонентов системы, так как даже при наличии современных ЭВМ имитация быстро становится слишком сложной. Поэтому необходимо иметь некоторую абстракцию, основанную на здравом смысле и допущениях о функционировании экосистемы.
При использовании системной динамики в моделировании выделяют три главных этапа:
· Во-первых, нужно установить, какое именно динамическое свойство системы представляет интерес и сформулировать гипотезы о взаимодействиях, порождающих данное свойство.
· Во-вторых, компьютерная имитационная модель должна быть построена таким образом, чтобы она дублировала элементы поведения и взаимодействий, определенные как существенные для системы.
· В-третьих, когда мы убедимся в том, что поведение модели достаточно близко к поведению реальной системы, мы используем модель, чтобы понять последовательность изменений, наблюдаемых в реальной системе, и предложить эксперименты, которые нужно поставить на стадии оценки потенциальных стратегий, т.е на следующем этапе системного анализа.
Основные характеристики динамических моделей состоят в том, что экологическая система рассматривается в динамике во времени, т.е. происходит изменение количественных характеристик (численности, биомассы) в динамике, описываемой непрерывными функциями.
Трудности динамических моделей заключаются в том, что не всегдалегко предсказать поведение даже самых простых моделей. Достаточно лишь одной нелинейности и двух петель обратной связи, чтобы поведение модели противоречило нашим интуитивным представлениям о системе. С другой стороны, ничего не стоит построить модель, не совпадающую с действительностью или неустойчивую. Еще одна трудность связана с тем, что для выяснения механизма функционирования модельной системы обычно необходимо провести много специальных экспериментов с моделью. Например, всегда приходится проверять поведение модели в ответ на одновременное изменение двух или более входных переменных и только в редких случаях достаточно проверить реакцию на изменение лишь одной переменной.
Трудности, связанные с предсказанием поведения динамических моделей, заметно снижают их роль в дальнейшем развитии теории. Естественно, что наибольшие трудности в построении математических моделей связаны с проверкой основных допущений, необходимых для применения модели, но часто эта проверка бывает более легкой и математически строгой, нежели поиск сложных типов поведения и разрывностей в динамических моделях. Еще один недостаток в том, что они не всегда дают оценки значений основных параметров, особенно когда их число достаточно велико, а использование метода итераций довольно.
Динамические модели по своей природе и математической структуре нацелены в основном на получение детерминистских решений. Правда, в них могут включаться стохастические элементы.
Динамические модели могут быть особенно полезны на ранних стадиях системного анализа сложных экологических систем, поскольку они направлены на выявление основных связей в системе и тех переменных и подсистем, которые являются ключевыми. На более поздних этапах целесообразнее сосредоточить усилия на использовании какого-либо другого семейства моделей, именно поэтому в системном анализе выделена стадия получения альтернативных решений проблемы.
Матричные модели
Использование матричного исчисления для описания роста сложных популяций началось в основном после работ Лесли (Уильямсон, 1975). Они представляют собой одну из удобных форм описания популяционных систем для практических вычислений.
Матрица есть прямоугольная таблица, размером i×j, где i – число строк, j – число столбцов, (например 3×4). Каждое из i×j чисел называется элементом. Если в целом матрица обозначается А, то aij – это элемент i-той строки, j-того столбца А.
(3.6)
Матрицы бывают нескольких типов: квадратные, единичные, нулевые, симметричные. Кроме того, существуют матрицы вектор-столбец и вектор-строка, а также состоящая из одного элемента – скаляр, напримерА=3.
Записывать массивы чисел в виде матриц удобно потому, что это позволяет оперировать с ними так же, как и с обычными числами, т.е. скалярами. Например, сложение и вычитание двух матриц состоит в сложении или вычитании всех соответствующих элементов этих матриц. Умножение и деление матриц не столь просты, но тоже представляют вполне определенные математические операции. Матричная алгебра является одной из важнейших областей современной математики и экологам, использующим системный анализ необходимо ее знать.
Квадратные матрицы обладают одним важным свойством: для любой такой матрицы существуют собственные числа (l) и собственные векторы (n), которые удовлетворяют уравнению A×v=l×v, где А – квадратная матрица, v – вектор столбец, l – скаляр, главное собственное число. В общем случае, если матрица имеет размер n×n, существует n собственных чисел и векторов. Они играют важную роль при выяснении специфических свойств исходной матрицы. Существует много методов их определения и, как правило, без ЭВМ это невозможно.
Один из ранних вариантов матричной модели был разработан Льюисом и Лесли в начале сороковых годов прошлого века. Как детерминистская модель она предсказывает будущую возрастную структуру популяции самок по известной структуре в настоящий момент времени и гипотетическим коэффициентам выживания и плодовитости. Популяцию разбивают на n+1 возрастных групп (т.е. 0,1,2,…,n), причем каждая группа состоит из особей одного возраста, так что самая старшая группа или группа, в которой все доживающие до данного возраста животные вымирают, имеет возраст n. Модель представляется матричным уравнением:
(3.7)
Согласно этому уравнению численности животных возрастных классов в момент времени t+1 можно получить, умножив численности возрастных классов в момент времени t на матрицу, элементами которой являются коэффициенты плодовитости и выживания для каждого возрастного класса. Величины fi (i=0,1,2….,n) представляют число самок, производимых одной самкой i-того возрастного класса, а pi(i=0,1,2….,n-1) – вероятность того, что самка i-того возрастного класса доживет до возраста i+1.
Менее очевидно то, что поведение этой модели можно предсказать, анализируя некоторые формальные свойства матрицы в уравнении
А×аt=аt+1, (3.8)
где at – вектор-столбец, представляющий возрастную структуру популяции в момент t, а аt+1 – вектор-столбец, представляющий возрастную структуру в момент t+1.
Во-первых, последовательно умножив уравнение на матрицу А, легко получить более общее уравнение для численности возрастных классов к моменту времени t+k:
at+k=Ak×at. (3.9)
Во-вторых, поскольку матрица А квадратная с n+1 строками и столбцами, она имеет n+1 собственных чисел и собственных векторов. Элементы А суть положительные числа или нули, т.к. ни fi,, ни pi не могут принимать отрицательных значений, в этом случае наибольшее собственное число и все координаты соответствующего ему собственного вектора также положительны и имеют определенный экологический смысл.
Пример. Простейшая модель Уильямсона (1981):
(3.10)
Исходная популяция состоит из одной самки старшего возраста, что отражено в векторе-столбце в левой части уравнения. По прошествии одного временного интервала в популяции будет уже 12 самок младшего возраста, поскольку
(3.11)
Повторное применение модели, когда вектор для предшествующей популяции умножается на коэффициенты плодовитости и выживания, дает такие результаты:
, 
,
(3.12)
и т.д.
Рисунок 3.2–Предсказание численности самок младшего, среднегои старшего возраста
Каждое животное старшего возраста, прежде чем умереть, успевает произвести в среднем 12 потомков, каждое животное среднего возраста – прежде чем умереть или перейти в следующий класс (вероятности этих событий одинаковы), производит в среднем 9 потомков. Молодые особи не производят потомства и с вероятностью 1/3 попадают в среднюю возрастную группу. На рис. 3.2 в логарифмическом масштабе показаны изменения численности каждой возрастной группы для первых 20 временных интервалов. С момента времени, до которого наблюдаются колебания численностей, предсказанные численностиэкспоненциально возрастают, причем соотношение между численностями животных разных возрастов остается постоянным.
Главное собственное число и собственный вектор можно найти простым методом последовательных приближений. Главное собственное число дает скорость, с которой возрастает размер популяции, в нашем случае это 2, т.е. за каждый временной интервал размер популяции удваивается. В общем случае, если l – главное собственное число,
A×v=l×v, (3.13)
где l – устойчивая возрастная структура популяции, причем численность возрастных классов представлена в виде относительных величин. Если построить график зависимости логарифма размера популяции (численности) от времени, то наклон этого графика после достижения устойчивой структуры будет равен Lnl – внутренней скорости естественного прироста. Зная главное собственное число, можно по уравнению оценить также число особей, которых необходимо изъять из популяции, чтобы размер ее стал равен исходному (здесь H – доля особей в %, изымаемых из популяции).
, (3.14)
В свою очередь, соответствующий главному собственному числу собственный вектор отражает устойчивую возрастную структуру популяции.
. (3.15)
В нашем примере этот вектор указывает на то, что между численностью животных младшего, среднего и старшего возрастных классов в популяции, достигшей устойчивой возрастной структуры, имеется определенное соотношение.
Марковские модели
Марковские модели – один из типов стохастических моделей. Они состоят в близком родстве с матричными моделями, т.к. их основная конструкция – матрицы, но элементами которых являются не детерминированные, а вероятностные переходы из одного состояния в другое. Суммы вероятностей по всем строкам равны 1.
Марковская модель первого порядка – это модель, в которой будущее развитие системы определяется ее текущим состоянием и не зависит от того, каким путем система пришла в это состояние. Последовательность результатов, получаемых из такой модели, часто называют марковской цепью. Применение такой модели к практическим ситуациям требует выполнения трех основных условий:
1. Система должна допускать классификацию на конечное число состояний.
2. Переходы должны происходить в дискретные моменты времени, правда, они должны быть достаточно близкими, чтобы для моделируемой системы время можно было бы считать непрерывным.
3. Вероятности не должны меняться во времени.
Возможны и модификации этих условий, однако математическая сложность модели при этом будет возрастать. Иногда используют вероятности, зависящие от времени, и непостоянные промежутки времени между переходами.
Особенно велико потенциальное значение марковских моделей в экологии, в тех случаях, когда изучаемые системы проявляют марковские свойства и из анализа модели можно получить такие, например важные выводы:
1. Алгебраический анализ матрицы перехода выявляет существование переходных множеств состояний, замкнутых множеств состояний и поглощающих состояний. Дальнейший анализ позволяет разбить переходную матрицу на блоки, которые исследуются по отдельности, что упрощает изучение экологической системы.
2. Анализ переходной матрицы позволяет вычислить среднее время перехода из одного состояния в другое и среднюю длительность пребывания в конкретном состоянии, если оно достигается.
Когда существуют замкнутые или поглощающие состояния, можно вычислить вероятность пребывания в замкнутом множестве или среднее время поглощения.
Экологический смысл этих понятий схематически иллюстрирует рис. 3.3., где показана типичная сукцессия (Джефферс, 1981).
Рисунок 3.3– Схематическое изображение переходных, замкнутых
и поглощающих состояний
Переходным множеством состоянийявляется множество, каждое состояние которого может в конце концов быть достигнуто из любого другого состояния этого множества, но которое покидается навсегда, если система переходит взамкнутое множество состоянийили впоглощающее состояние.
Замкнутое множество состоянийотличается от переходного тем, что оно не может быть покинуто, если система перешла в одно из состояний замкнутого множества.
Поглощающимявляется состояние, которое, будучи достигнуто, уже не покидается, т.е. в нем происходит полное самозамещение. Среднее время первого достижения соответствует тогда среднему времени, необходимому для наступления конкретной стадии сукцессии, а среднее время поглощения – среднему времени достижения устойчивой композиции.
Наиболее перспективным является применение марковских моделей для моделирования сукцессий экосистем.
Для построения моделей марковского типа необходимо следующее:
1. Некая разумная классификация состояний сукцессии по определенным категориям. Здесь будут полезны и многомерные модели.
2. Данные для определения переходных вероятностей или скоростей, с которыми состояния переходят со временем из одной категории данной классификации в другую.
3. Данные о начальных условиях, сложившихся в некоторый фиксированный момент времени, обычно после известного возмущения (катаклизмы, катастрофы и т.п.).
Выбор между марковскими и другими моделями часто зависит от целей исследований, но там, где можно применить прямой марковский подход, появляется возможность провести дальнейший алгебраический анализ, позволяющий лучше понять характер экологических процессов и вычислить средние времена достижения и поглощения, а также степени стабильности и сходимости для определенного состояния, что дает конкретную информацию, имеющую отношение к экологии и управлению.
Преимущества моделей марковского типа следующие:
1. Такие модели довольно легко строить на основе данных по сукцессиям.
2. Марковские модели не требуют глубокого понимания внутренних механизмов динамических изменений в системе, т.е. выступают как конкретный ориентир для дальнейших исследований.
3. Основная матрица переходных вероятностей отображает главные параметры динамических изменений в системе таким образом, который доступен лишь немногим моделям других типов.
4. Результаты анализа марковских моделей легко представить графически, что делает их более наглядными и понятными.
5. Вычислительные потребности при исследовании марковских моделей довольно скромны, особенно при небольшом числе состояний.
К недостаткам таких моделей можно отнести следующее:
1. Отсутствие зависимости от функциональных механизмов, что снижает привлекательность моделей для экологов.
2. Отклонение от стационарности, в предположении которой получены марковские цепи первого порядка. Хотя в случае прямых марковских моделей это в принципе и возможно, но приводит к непомерно большим трудностям в анализе и вычислениях.
3. В отдельных случаях имеющихся данных недостаточно для того, чтобы достоверно оценить вероятности или скорости перехода.
4. Как и в других моделях выяснение адекватности модели зависит от возможности предсказать поведение системы. Сделать же это для процессов, охватывающих достаточно длительные периоды времени, довольно трудно.
Главная задача при построении марковских моделей состоит в сборе данных для вычисления переходных вероятностей и создания переходных матриц, для чего требуется информация об изменениях, происходящих за определенные интервалы времени, и реакциях на различные типы возмущений. Приведем пример (табл. 3.2) применения марковской модели для анализа сукцессии экосистемы болота из работы Джефферса (1981).
Состояние 1 – соответствует наиболее влажной фации; 2 – отвечает более сухой фации с ассоциацией calluna vulgaris; 3 – соответствует более или менее укоренившемуся лесу; 4 – соответствует стадии, на которой более сухие фации спорадически выедаются крупными травоядными.
Участки, соответствующие первому состоянию (болото) через 20 лет (шаг модели) с вероятностьюР=0,65, остаются такими же, с Р=0,29 превращаются в calluna vulgaris, с Р=0,06 – в лес. Аналогичные изменения происходят и по остальным пунктам таблицы.
Таблица 3.2.– Оценка вероятностей переходов между четырьмя возможными состояниями за период в 20 лет
| Начальное | Вероятность перехода в конечное состояние | |||
| 1. Болото | 2. Callunavulgaris | 3. Лес | 4. Участок, выедаемый крупными травоядными | |
| 1. Болото 2. Callunavulgaris 3. Лес 4. Участок, выедаемый крупными травоядными | 0,65 0,3 0 0 | 0,29 0,33 0,28 0,4 | 0,06 0,3 0,69 0,2 | 0 0,07 0,03 0,4 |
Таким образом, ни одно из указанных четырех состояний не является замкнутым или поглощающим.
В целом набор этих состояний отражает переход от болота к лесу – переход, на который накладываются внешние возмущения, обусловленные выеданием растительности травоядными. Когда поглощающие состояния отсутствуют, марковский процесс является эргодической цепью и все следствия из матрицы переходных вероятностей мы можем получить, используя основные свойства марковской модели.
Приведенная матричная модель представляет собой переход из состояния в состояние за один временной шаг (20 лет).
Вероятности переходов за два временных шага можно получить, умножая одношаговую матрицу саму на себя, так что в простейшем случае двух состояний соответствующие вероятности задаются матрицей:
(3.16)
или в сжатой (матричной) форме:
Р(2) = Р×Р. (3.17)
Трехшаговые матрицы получаются умножением матрицы второго порядка на матрицу первого:
Р(3) = Р(2)×Р. (3.18)
Для общего случая из n шагов имеем
Р(n) = Р(n-1)×Р. (3.19)
Для нашей матрицы вероятности переходов за два шага равны:
. (3.20)
Если матрицу вероятностей переходов последовательно возводить в степень до тех пор, пока каждая ее строка не станет такой же, как и все остальные, образуя некоторый фиксированный вектор вероятностей, мы получим так называемую регулярную переходную матрицу. Эта матрица показывает, до какой степени вероятность перехода из одного состояния в другое не зависит от начального состояния, а фиксированный вектор вероятностей дает стационарное распределение вероятностей всех состояний. В нашем примере это вектор [0,2177 0,2539 0,3822 0,1462]. Таким образом, данная экосистема достигает в конце концов состояния равновесия, в котором ≈22 % площади занято болотами и приблизительно по 25, 38 и 15 % занимают сообщества calluna vulgaris, лес и участки, выедаемые травоядными.
При отсутствии поглощающих состояний (как в нашем случае) нас интересуют средние времена первого достижения любого состояния, например, среднее время превращения болота в calluna vulgaris, в лес, либо в выедаемый травоядными животными участок. В результате вычислений, которые здесь не приводятся, получаем матрицу средних времен первого достижения.
. (3.21)
Поскольку каждый временной шаг равен 20 годам, среднее время, необходимое для того, чтобы участок, где преобладает callunavulgaris, превратился в болото, составляет 9,566×20=191 г. Аналогично среднее время, необходимое для превращения леса в участок, на котором преобладает callunavulgaris, составляет 4,107×20=82 г. Таким же образом можно вычислить и другие времена.
Наконец, зная матрицу времен и вектор вероятностей, легко найти вектор средних времен первого достижения в равновесии:
½ 10,385 3,676 3,627 25,351½.
И вновь, поскольку шаг равен 20 годам, среднее время, необходимое для того, чтобы случайно выбранный участок превратился в болото, составляет 10,385×20=208 лет, а чтобы он превратился в участок, на котором преобладает вид calluna vulgaris, в лес или участок, выедаемый травоядными, в среднем соответственно 74 г., 73 г., 507 лет.
Здесь, как и во многих других математических моделях, основные свойства модели дают дополнительную информацию о поведении моделируемой системы и тем самым позволяют избежать длительных экспериментов для определения свойств эмпирической модели динамики.
Оптимизационные модели
Для специалиста по системной экологии очень важно представлять себе возможности моделей, когда работа находится на стадии выбора пути решения задачи. Столь необычное слово «оптимизация» обозначает отыскание максимума либо минимума какого-то математического выражения или функции, когда некоторые их переменные можно изменять в определенных пределах. Если бы мы хотели найти только максимум, мы могли бы назвать процесс максимизацией. И наоборот, отыскивая только минимум, мы могли бы использовать слово минимизация. Математически одну из этих операций всегда можно превратить в другую, так что в том, что оба процесса рассматриваются как один, есть определенная логика. Практически любые модели могут быть использованы при отыскании тех или иных максимумов или минимумов. Будет ли это использование иметь смысл, целиком зависит от конкретной задачи, но такие ситуации, когда необходимо изучить возможность увеличения продуктивности некоторой экологической системы путем изменения окружающей среды или смены методов управления, возникают в экологии довольно часто. Одна из главных причин применения моделей в том и состоит, что мы должны уметь предвидеть результаты этих изменений.
С помощью динамической модели, например роста дрожжей в смешанной культуре, описанной с помощью дифференциальных уравнений, мы можем попытаться определить соотношение между исходными количествами двух видов дрожжей, при котором продуцируется максимум дрожжевых клеток. Определив экспериментально основные параметры моделей, мы можем последующие эксперименты с целью отыскания нужных соотношений проводить уже на моделях.
В матричных моделях, экспериментируя с несколькими различными возрастными структурами популяции и интенсивностями ее эксплуатации, мы можем определить оптимальное значение некоторой целевой функции, хотя сами матричные методы при заданных начальных условиях определяют стационарные состояния и коэффициенты сбора урожая.
Интересные возможности для экспериментирования предоставляют и стохастические модели. Моделируя поведение изменения экосистем верхового болота, можно исследовать влияние изменения переходных вероятностей на продолжительность времени, в течение которого исследуемый участок остается в каком-то конкретном состоянии, применяя для этих целей матрицы переходных вероятностей.
Труднеепредусмотреть оптимизацию в многомерных моделях, но, по крайней мере, в одном смысле эти модели уже обнаруживают оптимальные условия, определяющие связи. Так, например, дискриминантные функции представляют собой линейные функции исходных переменных, которые обеспечивают наилучшую (т.е. оптимальную) дискриминацию между априорными группами. Аналогичным образом канонические корреляции определяют такие линейные функции двух наборов переменных, которые обладают наибольшими корреляциями.
Совершенно естественнымявляется желание сформулировать модель так, чтобы облегчить отыскание оптимальной комбинации ключевых переменных, и основные математические формулировки такого рода были разработаны независимо в тех ранних приложениях математических методов к практическим задачам, которые известны сейчас под названием «исследование операций». В этой модели центральное место может занимать линейная целевая функция
Y = A1×X1 + A2×X2 +........ + An×Xn =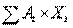 
(3.22)
и для этой модели определяется максимум или минимум функции при одном или более ограничениях, которые также выражены в виде линейных функций, хотя исходно это могут быть просто неравенства, например
b1×X1 + b2 ×X2 ≥ Z. (3.23)
Часто имеются неявные ограничения, состоящие в том, что Хiне могут быть отрицательными.
Когда переменных только две, задачи оптимизации довольно легко решаются графическими методами. Для более чем двух переменных задача сильно усложняется, и обычный подход к ее решению предполагает использование так называемого «симплекс-метода». Прежде всего, путем введения вспомогательных переменных; ограничения, выраженные в виде неравенств, заменяются линейными уравнениями. Но ограничения, состоящие в том, что все переменные должны быть больше нуля, остаются прежними. Затем ищется любое допустимое решение задачи, и, как только оно найдено, итеративным методом пытаются улучшить это решение, т.е. приблизить его к определенному оптимуму целевой функции с помощью малых изменений значений переменных. Эта итеративная процедура продолжается до тех пор, пока нельзя будет получить никакого дальнейшего улучшения.
Одно из преимуществ оптимизационных моделей состоит в том, что они всегда освещают два немаловажных аспекта проблемы. Полученное решение дает значение переменных целевой функции, при которых эта функция достигает максимума или минимума, в зависимости от того, как поставлена задача. Однако, помимо этого, метод указывает и то ограничение, которое нужно ослабить, чтобы улучшить оптимальное значение целевой функции. В результате этого экспериментатор может тщательнее проверить постановку задачи и, в частности, свои оценки коэффициентов при переменных в целевой функции и природу указанного ограничения. Если окажется, что можно улучшить оценки или ослабить ограничение, то он сможет найти еще лучшее решение.
Пример. Оптимальные стратегии хищника.Предположим, что хищник существует в гнезде в точке А и имеется два потенциальных источника пищи, расположенных на участках В и С. Время, необходимое для того, чтобы добраться до участков В и С и возвратиться с единицей добычи, полагается двум и трем минутам соответственно. С другой стороны, на участке В хищник затрачивает на поимку добычи х1 две минуты, тогда как на участке С ему требуется лишь одна минута, чтобы поймать единицу добычи х2. Энергетическая ценность одной единицы х1 оценивается в 25 Дж, а единицы х2 – в 30 Дж.
Если мы введем теперь ограничение, состоящее в том, что на путь из гнезда в любой из участков и обратно хищник может затрачивать не более 120 минут в сутки и что на поиск жертв он может тратить не более 80 мин в сутки, то мы придем к классической задаче линейного программирования. Упомянутые ограничения записываются в виде неравенств:
2х1 + 3х2 ≤ 120 – для времени в пути и
2х1 + 1х2 ≤ 80 – для времени поиска пищи.
Нужно записать также неявные ограничения х1 ≥ 0, х2 ≥ 0, так как хищник не может поймать отрицательное число жертв. При этих ограничениях мы хотим максимизировать целевую функцию
Z = (25х1 + 30х2) Дж.
Эту частную задачу легко решить графически, воспользовавшись записанными в виде неравенств ограничениями. Ограничение по времени в пути показывает, что если х1 равно нулю, то х2 может быть не более 40 единиц. Точно так же, если х2 равно нулю, то х1 может быть не более 60 единиц. Комбинации предельных значений х1 и х2 можно представить в виде прямой, соединяющей две точки – (х1 = 60; х2 = 0) и (х1 = 0; х2 = 40) (рис. 3.4).
Рисунок 3.4– Графическое решение простой задачи линейного программирования
Применив аналогичные рассуждения к ограничению по времени поиска пищи, мы получим, что еслих1равно нулю, то х2 не может превышать 80 единиц, а если х2 равно нулю, то не может быть больше 40 единиц.
Все имеющие смысл решения лежат, таким образом, в четырехугольникеOPQR(см. рис. 3.4), а максимум целевой функции достигается в точке, которая наиболее удалена от начала координат в направлении, показанном стрелкой. Эта точка имеет координаты (х1=30; х2=20), так что максимальное значение целевой функции равно
Z = 25x1 + 30x2 = 1350 Дж.
Можно самостоятельно проверить, как влияет ослабление одного или обоих ограничений на целевую функцию, имея в виду, что самым важным при оптимизации часто является нахождение того ограничения, ослабление которого позволяет найти еще лучшее решение.
Данный пример, очень прост, и графический метод решенияобычно можно применять лишь в том случае, когда целевая функция и ограничения зависят от двух переменных; правда, такие решения нередко можно найти и для случая нескольких ограничений. Однако имеются эффективные алгоритмы для решения задач линейного программирования и, особенно для тех задач, которые возникли и сформулированы как задачи о перевозках, связанные с оптимизацией транспортировки различных материалов и полезных ископаемых. Но существует множество экологических проблем, которые можно выразить через модели линейного программирования. Большинство этих проблем связано с управлением природными ресурсами в сельском хозяйстве и лесоводстве, где линейное программирование применяется в исследованиях по управлению и планированию лесных запасов, при экономическом анализе мероприятий по улучшению качества древесных лесных пород и при анализе развития сельскохозяйственных предприятий и т.п. Однако не все задачи можно представить через линейные целевые функции и линейные ограничения, особенно в экологических исследованиях. Нелинейность же этих функций или ограничений– либо и того и другого– очень сильно затрудняетотыскание решений. К таким же трудностям приводят и постановки задач, при которых накладываются определенные ограничения на размеры скоплений, в которых могут быть сосредоточены единицы каких-то конкретных ресурсов. В связи с этим была разработана теория нелинейного программирования, хотя экологических моделей, построенных исключительно на основе этой теории, довольно мало.
Иногда крупномасштабные проблемы оптимизации можно подразделить на ряд более мелких задач, образующих последовательность во времени или в пространстве, или наоборот. Подобные постановки задач часто позволяют упростить процедуру отыскания решения, при этом нужно специально проверять, дает ли последовательность оптимальных решений подзадач приближение оптимального решения полной проблемы. Такой поиск наилучшего решения на каждом этапе известен под названием «динамического программирования». Математический аппарат, использующийся в таких моделях, довольно сложен, и поэтому примеры их успешного применения в экологии весьма немногочисленны.
Модели теории игр
С моделями математического программирования тесно связаны модели, которые основаны на теории игр. Простейшая из этих моделей – так называемая игра двух лиц с нулевой суммой. При этом имеется два множества интересов, одно из которых может представлять природу или какую-то другую внешнюю силу, а сама игра «замкнута» в том смысле, что все, что проигрывает один из игроков, выигрывает другой.
В той разновидности игры, с которой мы будем иметь дело, в центре анализа стоит простая матрица, показывающая, какие стратегии могут применять оба игрока и исходы возможных комбинаций этих стратегий. Пример такой матрицы приведен в табл. 3.2, которая дает возможные исходы игры с точки зрения человека, который не может вспомнить, является ли сегодняшний день днем рождения его жены! Он может применить две стратегии, а именно: либо купить цветы, либо прийти домой без цветов. У природы здесь тоже две стратегии, т.е. день рождения жены либо сегодня, либо в другой день.
Таблица 3.3.–Матрица игры, указывающая стратегии и исходы для задачи «Не сегодня ли день рождения жены?»
| Стратегия | Природа | ||
| День рождения не сегодня | День рождения сегодня | ||
| Муж | Без цветов С цветами | 0 1 | -10 1,5 |
Числа в таблице показывают исход игры с точки зрения мужа для каждой комбинации стратегий двух игроков. В соответствии с ними, если муж приходит домой без цветов и день рождения жены не сегодня, исход игры для него нулевой – он ничего не выигрывает и ничего не проигрывает. Если же он приходит без цветов, а день рождения жены сегодня, муж проигрывает достаточно много (-10), т.к. он забыл нечто, о чем следовало бы хорошо помнить. Если муж приходит домой с цветами, но день рождения не сегодня, имеется весьма скромный выигрыш, ценность которого быть может слегка уменьшается из-за ощущения, что он сделал то, чего можно было бы и не делать. Если муж приходит домой с цветами и день рождения жены именно сегодня, то выигрыш несколько больше (1,5), т.к. муж вспомнил о том, чего в общем-то и не должен был забывать.
Можно сказать, что данная игра обладает той характерной особенностью, которая в теории игр называется «седловой точкой». Попросту говоря, когда наибольший из минимумов по строке совпадает с наименьшим из максимумов по столбцу, игра имеет седловую точку и игрокам всегда следует придерживаться той чистой стратегии, которая стоит на пересечении соответствующих строки и столбца. В данной игре мужу в любом случае следует прийти домой с цветами!
Поиск седловых точек является весьма важным моментом теории игр; вероятность того, что эти седловые точки будут существовать у случайно выбранной матрицы, велика для матриц высоких порядков. В тех же случаях, когда никакой седловой точки не существует, можно показать, что решение следует искать в смешанных стратегиях. Это означает, что должны применяться две или более стратегии и что вероятности, с какими данные стратегии применяются, могут быть вычислены по матрице игры. Каждый раз во время игры выбор стратегии должен осуществляться случайно, но с фиксированными вероятностями для существующих стратегий.
Модели, основанные на теории игр, представляют собой интересный и пока еще мало изученный подход к решению стратегических задач. Разработка теории для более сложных игр с ненулевой суммой и игр многих лиц, где между игроками могут создаваться коалиции, представляет собой область исследований, заслуживающую особого внимания, в частности в экологических проектах, связанных с планированием и оценкой воздействия на окружающую среду
Вопросы для самопроверки:
1. Методы моделирования экосистем.
2. Математические модели.
3. Детерминистские модели.
4. Стохастические модели.
5. Динамические модели.
6. Матричные модели.
7. Марковские модели.
8. Оптимизационные модели.
Рекомендуемая литература: [3, 12-15, 22-34 ]
Дата добавления: 2018-04-15; просмотров: 1725; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!