Теоремы сложения и умножения вероятностей

ТЕОРИЯ ВЕРОЯТНОСТЕЙ (практика 1)

1. СЛУЧАЙНЫЕ СОБЫТИЯ

Множество событий. Классическое определение вероятности события

       В результате многократного повторения одних и тех же опытов (испытаний) можно наблюдать появление в них некоторого события. Такое событие, которое может произойти или не произойти в результате опыта, называется случайным.

       Во многих задачах рассматривается схема равновозможных событий. Например, при бросании игральной кости имеется одна и та же возможность выпадения любого от 1 до 6 очков на верхней грани. Другим примером может служить выбор номера объекта при контрольной выборочной проверке.

       Каждый из равновозможных результатов испытаний (опытов) называется элементарнымисходом или просто исходом. Элементарный исход может быть рассмотрен либо как самостоятельное событие, либо как составляющая более сложного события. Более строго: любое подмножество множества всех элементарных исходов Ω (в том числе и пустое) представляет собой определенное событие, которое обладает заданными свойствами. Например, на множестве элементарных исходов при бросании игральной кости можно выделить подмножество таких исходов, которые соответствуют выпадению четного числа очков, выпадению 7 очков и т.д.

       Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление такого события. В частности, появлению четного числа очков при бросании игральной кости соответствуют элементарные исходы с цифрами 2, 4, 6.

       Количественной мерой возможности появления некоторого случайного события служит вероятность.

       При классическом определении за вероятность события А принимают отношение числа благоприятствующих этому событию элементарных исходов (m)  к общему числу возможных исходов (n):

                                                 p(A) = .

       Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используют формулы комбинаторики.

       Если вычисляются такие комбинации из n элементов по m,  которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из n элементов по m  определяется по формуле

                                                       = .

       Если комбинации отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится по формуле

                                                       = .

       Если комбинации берутся из всех n элементов и отличаются только порядком следования, то они называются перестановками. Их число равно

                                                        P_n = n!.

 

   Пример 1. Брошена игральная кость. Событие А = «выпадение четного числа очков». Число всех возможных элементарных событий данного опыта n = 6. Благоприятными для А являются элементарные события е₂, е₄, е₆, т.е. m = 3. Следовательно, Р(А) = = = .

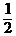  Пример 2. Одновременно бросили две кости. Выигрыш выплачивается, если сумма

           выпавших очков не меньше 10. Как велика вероятность выигрыша?

       А = «сумма очков ≥ 10». Число всех возможных элементарных событий данного опыта n = 36. Благоприятными для А являются элементарные события е₄₆, е₆₄, е₅₅, е₅₆, е₆₅, е₆₆, т.е. m = 6. Следовательно, Р(А) = = = .

   Пример 3. Игра в лото: «угадать k чисел из n», например, 6 из 49. Какова  

              вероятность получить главный выигрыш?

       А = «угадано k чисел из n». Число всех возможных элементарных событий данного опыта равно числу возможных выборок k чисел из n чисел без учета порядка и повторов, т.е сочетаний из n по k : N = . Благоприятным для получения главного выигрыша являются одно элементарное событие, т.е. m = 1. Следовательно,

 Р(А) = = . В случае лото «6 из 49» вероятность угадать все 6 чисел равна

    Р(А) = = = = .  

 

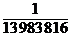1.1.1. На склад поступило 30 приборов, 5 из которых имеют заводской дефект. Случайным образом выбирается один прибор. Какова вероятность того, что он будет без дефекта? (5/6)

 

1.1.2. В коробке находится 6 одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки. Какова вероятность того, что сверла извлекутся в порядке возрастания их диаметров?  (1/720)

 

1.1.3. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и 2 известных вам магазина. Какова вероятность того, что в течение месяца они оба будут проверены? (0,0023)

 

1.1.4. На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от 1 до 10. Найти вероятность того, что среди 5 выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5.

 

Решение. Общее число возможных комбинаций для контрольного вскрытия равно числу сочетаний из  

 10 по 5, т.е. .

Число исходов, благоприятствующих данному событию, будем считать следующим  образом: исключим из рассмотрения вагоны 2 и 5. Из оставшихся 8 вагонов выбрать 3 вагона можно  способами. Вместе с вагонами 2 и 5 эти вагоны и представляют собой все пятерки вагонов, благоприятствующие рассматриваемому событию. Следовательно, искомая вероятность равна

                                                      p = = = = .

 

1.1.5. Изготовлена партия из 200 изделий, в которой оказались 3 бракованных. Произведена выборка из 5 изделий. Найти вероятности следующих событий:

      а)  в выборке не будет ни одного бракованного изделия; (0,926)

      б) в выборке будет одно бракованное изделие. (0,072)

1.1.6. Из 20 акционерных обществ (АО) четыре являются банкротами. Некто приобрел по одной акции шести АО. Какова вероятность того, что среди купленных им акций две окажутся акциями банкротов?

 

Решение. Общее число комбинаций выбора АО равно числу сочетаний из 20 по 6, т.е. .

Число благоприятствующих исходов определяется как произведение × , где первый сомножитель – это число комбинаций выбора АО-банкротов из четырех. Но каждой такой комбинации соответствуют  комбинаций АО, не являющихся банкротами. Следовательно, искомая вероятность

                                           p = = 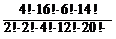≈ 0,28.

 

1.1.7. Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны 5 деталей. Какова вероятность того, что среди отобранных деталей 2 окажутся бракованными?    (0,07)

 

1.1.8. На склад привезли 50 ящиков комплектующих изделий для одного из видов аппаратуры, но среди них оказалось 4 ящика комплектующих для другого вида аппаратуры. Наудачу взяли 6 ящиков. Найти вероятность того, что в одном из этих шести ящиков окажутся некомплектные детали.    (0,345)

 

1.1.9. В партии из 15 однотипных приборов 5 приборов изготовлены на предприятии А, а 10 – на предприятии Б. Случайным образом отобрано 5 приборов. Найти вероятность того, что два из них изготовлены на предприятии А.    (≈0,4)

 

 

Геометрическая вероятность

 

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу

оставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством:

 

                                                    Р =  .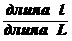

 

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру

 G наудачу брошена точка. Если предположить, что вероятность попадания точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g , то вероятность попадания точки на фигуру g определяется равенством:

Р =  .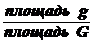

 

       Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V:

 

                                                     Р =  .

 

1.2.1. На отрезок ОА длины L числовой оси Ох наудачу брошены две точки: В(х)  

     и С(у), причем у ≥ х. Найти вероятность того, что длина отрезка ВС  

     меньше длины отрезка ОВ.

 

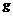
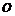
Решение.   Координаты точек В и С должны удовлетворять

неравенствам 0 ≤ х ≤ L, 0 ≤ у ≤ L, у ≥ х. Введем в рассмотрение

прямоугольную систему координат Оху (рис.7). В этой системе

указанным неравенствам удовлетворяют координаты любой точки,

принадлежащей прямоугольному треугольнику ОКМ. Т.о., этот

треугольник можно рассматривать как фигуру G, координаты 

точек которой представляют все возможные значения координат

точек В и С (прямоугольный треугольник ОКМ).                                                                     Рис.7.

Длина отрезка ВС должна быть меньше длины отрезка ОВ, т.е. должно

иметь место неравенство у – х < x, или у < 2x. Последнее неравенство выполняется для координат всех точек фигуры g, которые лежат ниже прямой у = 2x (прямая ON). Все эти точки принадлежат треугольнику ONM. Т.о., этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию

(А = «длина отрезка ВС меньше длины отрезка ОВ»). 

Искомая вероятность: площадь Р(А) =  =  = .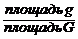 

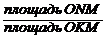1.2.2. Двое договорились встретиться на следующих условиях: в указанное 

место каждый из них приходит в любой момент времени между 13⁰⁰ и 14⁰⁰. Придя, ожидают не более получаса и уходят не позднее 14⁰⁰ . Какова вероятность того, что встреча состоится ?   

 

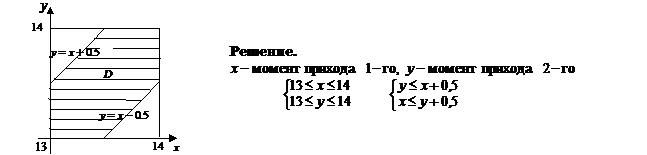
Р(А) =  =  = 0,75.

 

     1.2.3.  На окружности радиуса R зафиксирована точка А. Какова вероятность того, что случайно выбранная точка на окружности отстоит от точки А меньше, чем на R ?

 

        1.2.4. Противотанковые мины поставлены на прямой через 15м. Танк,

шириной 3м, идет перпендикулярно этой прямой. Какова вероятность того, что он подорвется ?

 

Решение. Чтобы не наскочить на мину, середина танка должна

отстоять от нее на расстоянии не менее, чем 1,5м. Т.о.,

длина допустимого интервала прохождения середины танка

через мины l_АВ = 15 – (1,5 + 1,5) = 12м. Следовательно,

вероятность не подорваться р_нп = = , а вероятность

подорваться р_п = 1 –  = . 

 

      1.2.5. В круг вписан квадрат. В круг наудачу бросается точка. Какова

вероятность того, что точка окажется вне квадрата ?

 

1.2.6.  В окружность вписан правильный треугольник. В круг наудачу бросается

точка. Какова вероятность того, что точка попадет в треугольник ?

 

        1.2.7. Наудачу взяты два положительных числа х и у, каждое из которых

не превышает 2. Найти вероятность того, что произведение ху будет не больше 1, а частное у / х не больше 2 ?   

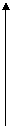
Решение.  Из неравенств 0 ≤ х ≤ 2, 0 ≤ у ≤ 2 следует, что случайный выбор

пары чисел х и у, удовлетворяющих этим неравенствам, можно интерпрети-

ровать как случайный выбор точки (х, у), принадлежащей квадрату 0 ≤ х ≤ 2,  

0 ≤ у ≤ 2, площадь которого S = 4.

Неравенства ху ≤ 1 => y ≤     и 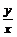≤ 2 => y ≤ 2х (вместе с неравен-

ствами 0 ≤ х ≤ 2, 0 ≤ у ≤ 2) геометрически представляют собой фигуру, ко-

ординаты точек (х, у) которой удовлетворяет условию задачи.

Площадь данной фигуры

   s =  +  = + = + ln2 – ln = + 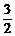ln2 ≈ 1,54.  Т.о.,

                                                   Р(А) = ≈  ≈ 0,385.

 

 

1.2.8.Какова вероятность того, что случайно выбранные два положительных

числа, не превышающих единицы, таковы, что их сумма меньше единицы, а произведение больше ?

Решение. Пусть одно из чисел х, другое – у. Имеем: 0 ≤ х ≤ 1, 0 ≤ у ≤ 1.  

Случайный выбор пары чисел х и у, удовлетворяющих этим неравенствам,

можно интерпретировать как случайный выбор точки (х, у), принадлежащей

квадрату 0 ≤ х ≤ 1, 0 ≤ у ≤ 1, площадь которого S = 1.

Неравенства х + у < 1 => y < 1 – x и x у >    => y >    

(вместе с неравенствами 0 ≤ х ≤ 1, 0 ≤ у ≤ 1) геометрически представляют

собой фигуру (заштрихованную на рисунке), координаты точек (х, у) 

которой удовлетворяет условию задачи.

Для вычисления площади данной фигуры найдем сначала точки пересечения

кривых y = 1 – x и y = :

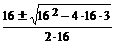1 – x =  => 16x² – 16x + 3 = 0 x_1,2 = =   => x₁ = , x₂ = .  

 s =  = ( x – – 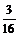ln x )|  = – – ln  – + + ln  = –  ln 3 ≈ 0,044.      

  Т.о.,          Р(А) = ≈  = 0,044.

 

 

1.2.9.На отрезок RT длины 1 наудачу бросаются две точки U(x), W(y), причем

х < y. Какова вероятность того, что из отрезков RU, UW и WR  (соответственно имеющих длины x, y – x, 1 – y) можно построить треугольник?

 

Решение.

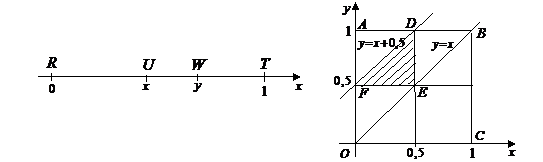
Событие А = «треугольник можно построить» произойдет, если будут выполнены условия: длина каждой из сторон меньше суммы длин двух других сторон, т.е. должны выполняться неравенства

                    x + (y – x) > 1 – y , x + (1 – y) > y – x, (y – x) + (1 – y) > x

или

y  > 0,5, y – x < 0,5, x < 0,5.

 

Эти неравенства из единичного квадрата OABC «вырезают» треугольник FDE (каждое из неравенств определяет соответствующую полуплоскость), который содержит точки(x, y), удовлетворяющие записанным выше неравенствам, т.е. из отрезков длиной x, y – x, 1 – y можно построить треугольник.

Неравенства

                                     0 ≤ х ≤ 1, 0 ≤ у ≤ 1, y > x,

 

определяют треугольник ОАВ, в который попадают все возможные точки, заданные условиями

задачи (т.е. те, у которых y > x).

Площадь треугольника FDE, очевидно, равна     S_FDE = 0,125 и    

1.2.10.Какова вероятность того, что корни уравнения x² + px + q = 0 будут

действительными, если коэффициенты p и q уравнения выбираются наудачу из отрезка [0;1]?

Решение.

1.2.11. Противник в течение часа делает один десятиминутный налет на

участок шоссе. В течение этого же часа нужно преодолеть этот участок шоссе. С

какой вероятностью можно избежать налета, если время преодоления опасного участка 5 минут?

Решение.

                     Р(А) =  = : 3600 ≈ 0,77.

Теоремы сложения и умножения вероятностей

       События называются несовместными, если они не могут появиться вместе в одном опыте. События называются совместными, если они могут появиться одновременно в одном опыте.

       Если множество событий состоит из попарно несовместных событий и одно из них в результате опыта произойдет обязательно, то такие события образуют полную группу событий. 

       Суммой событий называется событие, состоящее в появлении хотя бы одного из рассматриваемых событий.

 

       Теорема сложения вероятностей несовместных событий. Вероятность суммы

---

Дата добавления: 2018-04-15; просмотров: 3642; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!