Расчеты на сопротивление усталости

Расчеты на сопротивление усталости (или упрощенно — расчеты на усталость) имеют в технике очень большое значение. На усталость при изгибе рассчитывают валы и вращающиеся оси, на контактную усталость и изгиб рассчитывают зубья зубчатых передач, катки фрикционных пере­дач и многие другие детали. Потеря работоспособности и поломки дета­лей конструкций нередко происходят из-за усталости материала.

Расчеты на усталость нередко выполняются как проверочные.В результате получают фактические коэффициенты запаса прочности s,которые сравнивают с допускаемыми для данной конструкции коэффици­ентами запаса прочности [s] по условию:

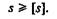
283

Обычно для деталей [s]= 1,3…3 и более в зависимости от вида и на­значения детали.

При симметричном цикле изменения напряжений коэффициент за­паса прочности определяют по следующим формулам:

для растяжения (сжатия)

для кручения

для изгиба

 

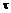где и — номинальные значения максимальных нормальных и каса­тельных напряжений; К — коэффициент снижения предела выносливости.

При работе деталей в условиях асимметричного цикла коэффициен­ты запаса прочности определяют по формулам Серенсена-Кинасошвили:

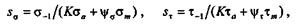
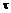где _а и _m ( _a и 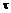_m) — амплитуда и среднее напряжение цикла; и — коэффициенты чувствительности к асимметрии цикла, вычисляемые по формулам:

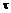где _-1 и ₀ ( _-1 и 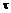₀) — пределы выносливости при симметричном и отну-левом циклах.

Ранее было установлено, что при прочих равных условиях предел выносливости при симметричном цикле ниже, чем при асимметричном, т.е. симметричный цикл является наиболее опасным. Поэтому при очень точных и ответственных расчетах применяют формулы Серенсена-Кинасошвили. При упрощенных расчетах можно полагать, что нормаль­ные и касательные напряжения изменяются по симметричному циклу. Это дает небольшое отклонение от точного расчета в сторону увеличения запаса прочности.

В случае сложного сопротивления (изгиб и кручение, кручение и растя­жение или сжатие), т. е. при упрощенном плоском напряженном состоянии, общий коэффициент запаса прочности s определяют из выражения

где s 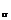 — коэффициент запаса прочности по нормальным напряжениям; s  — коэффициент запаса прочности по касательным напряжениям. Формулы для вычисления 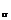s  и s   были приведены выше.

Сопротивление материалов при инерционной и ударной нагрузке

Расчеты при инерционной нагрузке.Расчеты с учетом инерцион­ных нагрузок ведутся известным из теоретической механики методом кинетостатики, основанном на принципе Даламбера. Согласно этому принципу все активные и реактивные силы, приложенные к телу, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовле­творяющую всем условиям равновесия. Таким образом, задачи динамики и сопромата решаются методами статики.

В качестве примера рассмотрим расчет тонкостенного кольца, рав­номерно вращающегося в своей плоскости с угловой скоростью 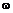(рис. 25.5, а). Полученная в результате расчета формула напряжений использу­ется при расчете ободов маховиков и напряжений в ремнях ременных передач.

При равномерном вращении нормальное ускорение любой точки

кольца а_п = v²/R = 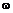²R, где v — окружная скорость, R — средний радиус кольца. Касательное ускорение а  = 0, так как 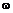 = const.

Применяя принцип Даламбера, приложим к каждому элементу коль­ца центробежную силу инерции. Эти силы распределены равномерно по окружности кольца и направлены по радиусу от центра. На единицу длины окружности кольца при­ходится сила инерции

q^ин=m_la_n,

где m₁= рА — масса единицы дуги кольца; А — площадь поперечного сечения; р — плотность материала кольца.

Подставляя значения, получаем

q^ин =pAv²/R.

Определим внутренние силы, возникаю­щие в поперечных сечениях кольца, для чего рассечем его по диаметру и рассмотрим рав­новесие оставленной части (рис. 25.5, б).

Поскольку кольцо тонкое, можно предпо-

2285

ложить, что нормальные напряжения распределены по его поперечному сече­нию равномерно, следовательно, кольцо работает на растяжение.

Определим продольные силы N , возникающие в поперечных сече­ниях. Для этого спроецируем все силы, действующие на полукольцо на ось у.На элемент кольца, соответствующий элементарному центральному углу dcp, приходится элементарная сила инерции 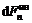, равная

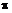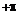Проекция этой силы на ось у равна произведению cos . По­скольку каждая из элементарных сил инерции направлена по радиусу и, следовательно, наклонена к оси у под разными углами, необходимо со­ставлять уравнения равновесия в интегральной форме (угол изменяется от - /2 до /2):

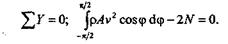
Отсюда

или

Вычислим нормальное напряжение в поперечном сечении кольца:

Отметим, что напряжения не зависят от площади поперечного сече­ния кольца и пропорциональны квадрату окружной скорости.

Запишем условие прочности:

 отсюда определим допускаемую окружную скорость:

 

Вычислим допускаемую окружную скорость, если кольцо изготовле­но из стали плотностью 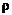= 0,8 10⁴ кг/ м³, допускаемое напряжение при растяжении [ _р] = 160 МПа. Тогда

Расчеты при ударной нагрузке.Ударом называется совокуп­ность явлений, возникающих при столкновении двух твердых тел. Удар может быть упругим и неупругим; в последнем случае ударяю-

286

щее тело не отскакивает от ударяемой упругой систе­мы, а продолжает двигаться вместе с ней. При ударе за очень малый промежуток времени (доли секунды) про­исходит резкое изменение относительной скорости со­ударяющихся тел, в результате чего возникают значи­тельные ударные или мгновенные силы.

Ударные нагрузки имеют в технике широкое при­менение, например, при ковке, штамповке и чеканке металла, забивке костылей, гвоздей и свай, в вибротех­нике. Сопротивление материалов при ударной нагрузке существенно отличается от поведения материала при статическом нагружении.

При рассмотрении примера действия ударной на­грузки будем считать, что напряжения не превышают предел пропорциональности, т.е. подчиняются закону Гука, а удар будем полагать абсолютно неупругим.

Рассмотрим напряжения и деформации при осевом ударе стержня постоянного сечения (рис. 25.6). Груз G падает с высоты h на недеформи-рующийся диск, укрепленный на конце стержня длиной l. Работа, произ­водимая грузом G при падении, равна потенциальной энергии U дефор­мации стержня:

Статическое удлинение стержня равно

тогда квадратное уравнение принимает вид

Решая это уравнение, получаем

где Е — модуль упругости материала стержня; l_д— его динамическое удлинение; А — площадь поперечного сечения стержня. Полученное выражение перепишем так:

(второй корень не определяется, так как он дает отрицательное значение для l_д).

Выражение для l_д  преобразуем к виду

287

Введем обозначение

где k_д— коэффициент динамичности. Тогда

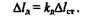
То есть наибольшее перемещение, вызываемое действием ударной на­грузки, равно произведению коэффициента динамичности на перемещение от статической нагрузки (в данном случае силы тяжести падающего груза).

На основании линейной зависимости (по закону Гука) между силами и перемещениями можно записать

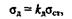
где — динамическое напряжение.

Определение перемещений и напряжений при ударе сводится, таким образом, к определению перемещений и напряжений, вызванных статиче­ски приложенной силой, равной силе тяжести падающего груза, и вычис­лению коэффициента динамичности.

Заметим, что полученные формулы верны как для случая продольного (осевого) удара по стержню, так и для случая поперечного удара по балке.

Рассмотрим случай внезапного приложения нагрузки, что равно­сильно действию груза, падающего с высоты h = 0. Тогда из формулы для определения коэффициента динамичности следует, что k_д= 2 , вследствие чего получаем l_д = 2 l_ст и _д = 2 _ст , т.е. перемещения и напряжения в результате действия внезапно приложенной силы вдвое больше, чем при статическом действии той же силы.

Из формулы для определения коэффициента динамичности видно, что с увеличением l_ст (т.е. уменьшением жесткости стержня) k_думень­шается. Поэтому в технике для смягчения ударов применяют пружины и рессоры — детали, имеющие малую жесткость (большую податливость).

Глава 26

ПРОДОЛЬНЫЙ ИЗГИБ

Общие сведения

Продольным изгибом называется изгиб первоначально прямолиней­ного стержня вследствие потери устойчивости под действием цен­трально приложенных продольных сжимающих сил. Продольный изгиб

288

возникает при достижении сжимающими силами и напряжениями критического значения.

Расчеты на прочность и жесткость, приведен­ные в предыдущих главах, делались в предположе­нии, что при деформации конструкции между внешними нагрузками и вызываемыми ими внут­ренними силами существует устойчивая форма равновесия, при которой малым возмущающим воздействиям соответствуют малые отклонения конструкции от первоначальной формы. Нагрузки, при превышении которых происходит потеря устойчивости (критическое состояние), на­зывают критическими. Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.

Рассмотрим тонкий стальной стержень, длина которого значительно больше поперечных размеров, сжимаемый силой F,немного большей критической силы F_кр(рис. 26.1).

Применяя метод сечений, убеждаемся, что в результате искривления оси в поперечных сечениях стержня возникают два внутренних силовых фактора — продольная сила N = F иизгибающий момент М_и.

Таким образом, искривленный стержень испытывает сочетание де­формаций центрального сжатия и изгиба.

При сжимающих силах, даже немного превышающих критическую силу, напряжения изгиба могут непосредственно угрожать прочности конструкции. Поэтому критическое состояние конструкции считается недопустимым.

Для обеспечения устойчивости необходимо, чтобы действующая на стержень сжимающая сила F была меньше критической F_кр.

Обозначим допускаемую сжимающую силу [F],тогда

где [s_y] — допускаемый коэффициент запаса устойчивости.

Очевидно, что устойчивость стержня обеспечена, если [s_y] > 1. Зна­чение коэффициента запаса устойчивости зависит от назначения стержня и его материала. Обычно для сталей [s_y] = 1,8...3; для чугунов [s_y]= 5...5,5; для дерева [s_y]= 2,8...3,2.

Формулы Эйлера и Ясинского

Для расчетов стержней на устойчивость необходимо знать способы определения критической силы F_кр.

289

Первые исследования устойчивости сжатых стержней были проведены ака­демиком Петербургской Академии наук Леонардом Эйлером (1707—1783). Ака­демик С. И. Вавилов писал: «Вместе с Петром I и Ломоносовым Эйлер стал доб­рым гением нашей Академии, определившим ее славу, ее крепость, ее продуктив­ность». В дальнейшем большая работа в области теоретического и эксперимен­тального исследования вопросов устойчивости была проведена русским ученым, профессором Петербургского института инженеров путей сообщения Ф. С. Ясин­ским (1856—1899)у опубликовавшим в 1893 г. большую работу «Опыт развития продольного изгиба».

Л. Эйлером была получена формула для определения величины кри­тической силы F_кр.

Приведем ф о р м у л у Эйлера без вывода:

где Е — модуль упругости первого рода; I_min — наименьший из осевых

моментов инерции сечения, поскольку искривление стержня происходит в плоскости наименьшей жесткости, в чем нетрудно убедиться, сжимая продольной силой слесарную линейку; l_п — приведенная длина стержня;

где l— длина стержня;  — коэффициент приведения длины, зависящий от способа закрепления концов стержня.

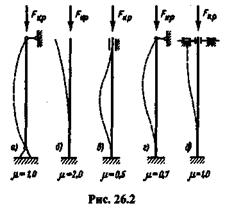
На рис. 26.2 показаны наиболее часто встречающиеся способы за­крепления концов стержня и приведены значения : 1) оба конца стержня закреплены шарнирно и могут сближаться (а); 2) нижний конец жестко защемлен, верхний свободен (б); 3) оба конца жестко защемлены, но мо­гут сближаться (в); 4) нижний конец закреплен жестко, верхний — шар­нирно, концы могут сближаться (г); 5) нижний конец закреплен жестко,

верхний имеет «плавающую за­делку» (д).Заметим, что чем меньше , тем больше критиче­ская сила, а следовательно, и до­пускаемая сжимающая нагрузка. Например, сжимающая нагрузка стержня, жестко защемленного обоими концами (  = 0,5), может быть в 16 раз больше нагрузки стержня, защемленного одним концом ( = 2).

Вывод формулы Эйлера основан на законе Гука, кото­рый справедлив только до пре-

Определим наименьший радиус инерции imin поперечного се­чения стержня:

Перепишем формулу для так:

дела пропорциональности. Поэтому формулой Эйлера можно пользовать­ся не всегда. Для определения пределов применимости форму­лы Эйлера определим критическое напряжение , т.е. напряжение, ко­торое возникает в поперечном сечении площадью А стержня при дости­жении

критической силы:

 

Введем понятие гибкости стержня . Это безраз­мерная величина, характеризующая размеры стержня и способ закрепле­ния его концов. Окончательно получаем:

Формулу Эйлера можно применять только при выполнении условия

где _пц — предел пропорциональности материала стержня. Следователь­но, должно быть

Величину, стоящую в правой части неравенства, называют пре­дельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.

Условие применимости формулы Эйлера можно записать так:

т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости.

Вычислим значение _пред для низкоуглеродистой стали Ст3, для ко­торой _пц = 200 МПа, а Е = 2 10⁵ МПа:

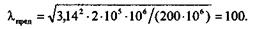
Для стержней из низкоуглеродистой стали формула Эйлера приме­нима, если их гибкость  100.

Аналогично можно вычислить значения предельной гибкости для других материалов. В частности, для чугуна _пред = 80; для дерева (сосна) _пред =110.

291

 

В тех случаях, когда гиб­кость стержней меньше пре­дельной, формула Эйлера ста­новится неприменимой и при расчетах пользуются эмпири­ческой формулой Ясин­ского

где а и  b — коэффициенты, зави­сящие от материала и опреде­ляемые по таблицам справочни­ков. В частности, для СтЗ при гибкостях = 40...100 можно принимать

а =310 МПа, b= 1,14 МПа. При гибкостях  < 40 стержни можно рассчитывать на сжатие, т.е. по формуле

Итак, при малых значениях  (  < 40) стержни из низкоуглеродистой стали рассчитывают на простое сжатие; при средних значениях (40 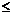< 100) расчет ведут по формуле Ясинского, а при больших ( 100) — по фор­муле Эйлера. График зависимости критического напряжения от гибкости для стержней из низкоуглеродистой стали изображен на рис. 26.3.

---

Дата добавления: 2018-04-15; просмотров: 945; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!