Закон сохранения механической энергии

⇐ ПредыдущаяСтр 41 из 72Следующая ⇒

Энергию взаимодействия между телами называют потенциальной. Потенциальной энергией обладают, например, натянутый лук со стрелой или сжатая пружина.

Всякая материальная точка, поднятая на определенную высоту h,также обладает некоторой энергией, которая называется энергией положения и является потенциальной энергией. Мерой потенциальной энергии в этом случае служит работа, которую произведет точка при свободном падении.

Полагая величину h небольшой по сравнению с размерами Земли, а поэтому считая постоянной силу тяжести G, получим выражение для потенциальной энергии П:

Потенциальная энергия тела, поднятого на определенную высоту, есть величина относительная, зависящая от системы отсчета, по отношению к которой вычисляется эта энергия.

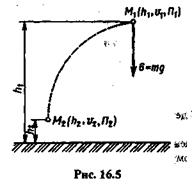
Пусть материальная точка массой т, падая под действием одной лишь силы тяжести G, в положении М₁находилась на высоте h₁имела скорость v₁и обладала потенциальной энергией П₁(рис. 16.5). В положении М₂ точка оказалась на высоте h₂, причем ее скорость стала v₂,а потенциальная энергия П₂.

При падении точки под действием одной лишь силы тяжести совершается работа

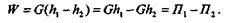
Согласно теореме, доказанной в предыдущем параграфе, эта работа равна изменению кинетической энергии:

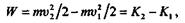
или

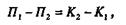
следовательно,

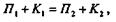
или

Это равенство является математическим выражением закона сохранения механической энергии, который формулируется так: при движении материальной точки под

154

действием одной лишь силы тяжести сумма потенциальной и кинетической энергий есть величина постоянная.

На основании закона сохранения механической энергии нетрудно доказать, что если тело боросить с поверхности Земли вертикально вверх, то его кинетическая энергия в нижнем положении будет равна потенциальной энергии в наивысшем положении.

Этот закон справедлив при движении под действием любой потенциальной силы; при действии же непотенциальных сил (например, силы трения) механическая энергия переходит в другие виды энергии.

Закон сохранения механической энергии является частным случаем общего закона сохранения материи и энергии, выведенного М. В. Ломоносовым (1711—1765). В установлении этого закона состоит одна из величайших для своего времени заслуг Ломоносова.

Ранее, в § 9.1, говорилось о возникновении в XX в. теории относительности, созданной А. Эйнштейном и к настоящему времени получившей широкое применение в науке и технике.

Одним из важнейших выводов теории относительности является закон пропорциональности энергии и массы тела. Математическое выражение этого закона имеет следующий вид:

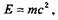
где Е — полный запас энергии тела (включающий в себя механическую, тепловую, химическую, электромагнитную, ядерную энергию, а также энергию частиц, входящих в состав атома); т — масса тела; с — скорость света.

На основании приведенного выше равенства, называемого формулой Эйнштейна, нетрудно подсчитать, что одному грамму массы соответствует 25 млн. кВгч энергии (1кВч ч = 3,6 10⁶ Дж).

Формула Эйнштейна имеет самое непосредственное отношение к открытию и использованию ядерной (атомной) энергии. Именно на основании этой формулы было установлено существование огромных запасов новых видов энергии и найдены пути ее использования. В 1954 г. в нашей стране была пущена первая в мире электростанция на атомной энергии мощностью 5000 кВт.

Пример 16.4. Материальная точка брошена с Земли вертикально вверх с начальной скоростью _{0 .}Пренебрегая сопротивлением воздуха, определить: 1) высоту h максимального подъема точки, 2) скорость , которую будет иметь точка на высоте h/2 при падении.

и в момент максимального подъема:

Решение. Для решения первой части задачи запишем выражения кинетической и потенциальной энергии в момент начала движения:

155

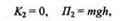
где m — масса материальной точки.

Согласно закону сохранения механической энергии,

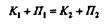
или

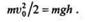
Отсюда, сократив обе части равенства на m, определим высоту h максимального подъема точки

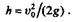
Для решения второй части задачи запишем выражения кинетической и потенциальной энергий на высоте h /2:

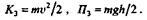
Согласно закону сохранения механической энергии,

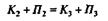
или

Отсюда, сократив обе части равенства на m и сделав приведение подобных членов, определим скорость:

Подставив найденное ранее значение h, получим

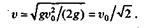
Глава 17

ОСНОВЫ ДИНАМИКИ СИСТЕМЫ

МАТЕРИАЛЬНЫХ ТОЧЕК

Дата добавления: 2018-04-15; просмотров: 559; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 36 37 38 39 404142 43 44 45 Следующая ⇒

Мы поможем в написании ваших работ!