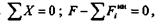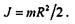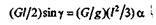Уравнение поступательного движения

Твердого тела

Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных между; собой. Всякое твердое тело можно считать неизменяемой механической системой материальных точек.

Силы взаимодействия точек данной системы называются внутренними; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, — внешними.

156

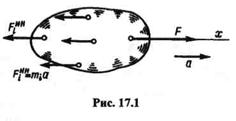
Пусть твердое тело массой т движется под действием силы F поступательно с ускорением а (рис. 17.1).

Разобьем тело на ряд материальных точек с массами m_t и применим принцип Даламбера (заметим, что внутренние силы в уравнения равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю). К каждой

материальной точке приложим силу инерции и составим

уравнение равновесия:

откуда

Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.

Согласно второму закону Ньютона, векторы силы Fи ускорения а совпадают по направлению, поэтому можно записать

Это и есть уравнение поступательного движения твердого тела.

Это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.

Уравнение вращательного движения

Твердого тела

Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением (рис. 17.2).

Разобьем тело на ряд материальных точек с массами т_i и применим принцип Даламбера. К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:

157

Моменты реакций подшипника и подпятника, а также сил относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом. Тогда

Выражение

называют моментом инерции тела

относительно оси и обозначают J:

Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояний от них до этой оси.

В результате получаем формулу

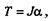
которая называется уравнением вращательного движения твердого тела. В этой формуле J — момент инерции тела относительно оси вращения.

Поясним более подробно новое понятие момента инерции тела.

Единица момента инерции:

Рассмотрим следующий пример.

Пусть требуется сообщить двум одинаковым шарам (рис. 17.3) одинаковое угловое ускорение . Так как r₁ > r₂,то J₁> J₂.Опытным путем, а также с помощью уравнения вращательного движения можно убедиться в том, что для сообщения этим системам одинакового углового ускорения потребуется приложить разные вращающие моменты:

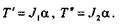
Разделим первое уравнение на второе:

Следовательно, чем больше момент инерции тела, тем

158

больший вращающий момент надо приложить, чтобы сообщить телу заданное угловое ускорение.

Из изложенного ясно, что момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, следовательно, момент инерции есть мера инертности вращающегося тела.

В качестве примера вычислим момент инерции тонкого однородного сплошного диска, радиус которго R,толщина s,масса т, относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (рис. 17.4).

Разобьем диск на элементарные кольца переменного радиуса r,шириной dr и толщиной s. Согласно определению, момент инерции такого кольца равен

где — плотность материала диска.

Так как масса диска т = R²s , то

Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:

Нетрудно понять, что момент инерции однородного сплошного прямого кругового цилиндра радиусом R и массой т любой высоты будет вычисляться по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить весь цилиндр плоскостями, параллельными основанию, на тонкие диски и просуммировать моменты инерции всех дисков.

Моменты инерции для некоторых других однородных тел определяются по формулам, которые приведем без выводов:

1) шар массой m, радиусом R относительно диаметра

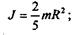
2) тонкий стержень массой m, длиной l относительно оси, проходящей перпендикулярно стержню через его конец,

159

3) тонкая сферическая оболочка массой т,радиусом R относительно диаметра

4) пустотелый вал массой т, наружным радиусом R и радиусом отверстия r относительно оси

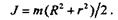
Момент инерции J_z тела относительно какой-либо оси z,параллельной центральной (т. е. проходящей через центр тяжести С тела), равен центральному моменту инерции J_С плюс произведение массы т тела на квадрат расстояния а между этими осями:

Из этой формулы следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси, т. е. центральный момент инерции.

Иногда момент инерции определяют по формуле

где r_и — радиус инерции тела;

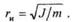
Физический смысл радиуса инерции заключается в следующем: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и разместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.

Удвоенный радиус инерции называется диаметром инерции:

В практике иногда вместо момента инерции пользуются понятием махового момента .

Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.

Единица махового момента

Между маховым моментом и моментом инерции существует простая зависимость

или

160

Пример 17.1.Тонкий однородный стержень силой тяжести G,длиной l = = 150 мм совершает колебательное движение в вертикальной плоскости под действием силы тяжести; точка подвеса совпадает с концом стержня (рис. 17.5). Определить угловое ускорение стержня в тот момент, когда он составляет с вертикалью угол = 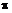/6 рад.

Решение. По условию задачи стержень однородный, следовательно, его центр тяжести находится посередине. Применим уравнение вращательного движения тела

Момент инерции стержня вычисляем по формуле

Вращающий момент равен моменту силы тяжести относительно оси вращения стержня:

Подставим выражения вращающего момента и момента инерции в уравнение вращательного движения:

и определим угловое ускорение:

Пример 17.2.Маховой момент ротора электродвигателя равен 2,7 Н м². Вращающий момент Т = 40 Н м. Определить время разгона, если конечная скорость вращения ротора 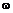= 30 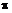рад/с.

Решение. Так как на ротор действует постоянный вращающий момент, то движение ротора будет равноускоренным. Запишем уравнение угловой скорости этого движения, учитывая, что 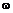₀ ⁼ 0:

откуда

Далее применим уравнение вращательного движения ротора

Из этого равенства определим время разгона, выразив момент инерции ротора через маховой момент, который равен 4gJ:

161

Дата добавления: 2018-04-15; просмотров: 2890; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 37 38 39 40 414243 44 45 46 Следующая ⇒

Мы поможем в написании ваших работ!