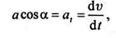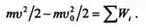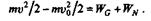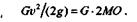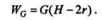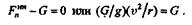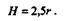Теорема об изменении кинетической энергии

⇐ ПредыдущаяСтр 40 из 72Следующая ⇒

Механической энергией называют энергию перемещения и взаимодействия тел. Механическая энергия бывает двух видов: кинетическая и потенциальная.

Кинетической энергией, или энергией движения, называется энергия, которой обладает всякая материальная точка при движении. Кинетическая энергия есть динамическая мера движения материальной точки.

Кинетическая энергия материальной точки равна половине произведения массы точки на квадрат ее скорости:

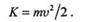
Кинетическая энергия — величина скалярная и всегда положительная. Единица кинетической энергии:

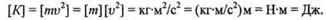
Кинетическая энергия имеет размерность работы. Связь между кинетической энергией и работой устанавливает теорема об изменении кинетической энергии, формулируемая так: изменение кинетиче-

150

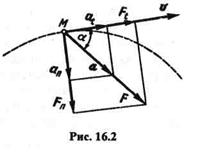
ской энергии материальной точки на некотором пути равно работе силы, приложенной к точке, на том же пути. Докажем эту теорему для самого общего случая движения материальной точки, т. е. для случая криволинейного движения под действием переменной силы (рис. 16.2). Запишем для этой точки основное уравнение динамики:

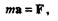
где F — действующая на точку сила; а — полное ускорение точки; т — масса точки.

Спроецируем это векторное равенство на направление скорости v точки:

Как известно из кинематики,

следовательно,

Умножив обе части равенства на бесконечно малое перемещение ds, получим

Выражение, стоящее в левой части равенства, преобразуем следующим образом:

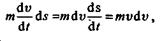
следовательно,

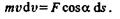
Интегрируя обе части этого равенства в пределах для скорости от ₀ до и для пути от 0 до s:

получаем

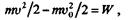
где W—работа силы F на пути s. Теорема доказана.

151

При замедленном движении ( < ₀) составляющая F_t, вызывающая касательное ускорение a_t, будет направлена в сторону, противоположную направлению вектора скорости v, и работа силы F будет отрицательной.

Составляющая F_n, вызывающая нормальное ускорение a_n, работы не совершает, так как эта составляющая в каждый данный момент перпендикулярна элементарному перемещению точки приложения силы F.

Если к материальной точке приложено несколько сил, то изменение кинетической энергии равно алгебраической сумме работ этих сил:

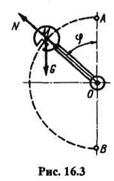
Пример 16.2. Главную часть прибора для испытания материалов ударом составляет стальная тяжелая отливка М, прикрепленная к стержню, который может вращаться почти без трения вокруг неподвижной горизонтальной оси О (рис. 16.3). Пренебрегая массой стержня, рассматриваем отливку М как материальную точку, для которой расстояние МО = 0,918 м. Определить скорость этой точки в наинизшем положении В, если она падает из наивысшего положения А с ничтожно малой начальной скоростью.

Решение. Обозначим силу тяжести отливки G. Применив принцип осво-бождаемости и теорему об изменении кинетической энергии и рассматривая отливку как материальную точку, на которую действуют сила тяжести G и реакция N стержня, направленная вдоль стержня, получим

Согласно теореме о работе силы тяжести, имеем

Работа реакции N равна нулю, так как момент этой силы относительно оси вращения стержня равен нулю. Силой трения, по условию, пренебрегаем.

Подставим это выражение работы в первую формулу и, учитывая, что ₀ = 0, получим

152

Сократим обе части равенства на G и подставим числовые значения, тогда

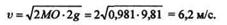
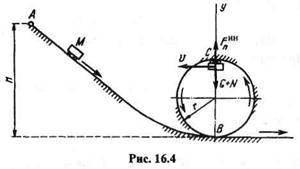
Пример 16.3. По рельсам, проложенным по пути АВ и образующим затем петлю радиуса г, катится вагонетка М силой тяжести G (рис. 16.4). С какой высоты Н нужно пустить вагонетку без начальной скорости, чтобы она могла пройти всю окружность кольца, не отделяясь от него?

Решение. Рассмотрим вагонетку как материальную точку. Для решения задачи применим теорему об изменении кинетической энергии на пути ABC:

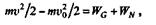
причем работа W_N нормальной реакции N рельсов равна нулю. На основании теоремы о работе силы тяжести

Так как, по условию, ₀ = 0, а т = G/g, то, подставив эти выражения в первую формулу, получим

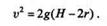откуда

(16.1)

Далее применим принцип Даламбера. Приложим к вагонетке центробежную силу инерции 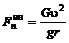, спроецируем действующие на вагонетку силы на ось у и составим уравнение равновесия:

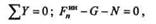
где N— реакция рельсов.

Очевидно, что наименьшее значение центробежной силы , при котором вагонетка не отделится от рельсов, будет при N = 0. При этом

Отсюда

(16.2)

Сравнивая выражения (16.1) и (16.2) и приравняв их правые части, получаем

откуда

Очевидно, что значение высоты Н,найденное из этого выражения, минимально.

Обращаем внимание на то, что при решении не принимаются во внимание силы трения и сопротивления воздуха. Поэтому для выполнения мертвой петли практически необходимо, чтобы Н > 2,5г.

153

Дата добавления: 2018-04-15; просмотров: 504; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 35 36 37 38 394041 42 43 44 Следующая ⇒

Мы поможем в написании ваших работ!