Теорема о работе равнодействующей

⇐ ПредыдущаяСтр 36 из 72Следующая ⇒

Теорема.Работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том лее участке пути.

Пусть к материальной точке М приложена система сил (F₁, F₂, F₃,…, F_n), равнодействующая которых равнаF 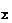(рис. 15.3).

Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,

Спроецируем это векторное равенство на касательную к траектории, тогда

Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем это равенство в пределах какого-то конечного перемещения s:

что дает равенство

или сокращенно

Теорема доказана.

142

Пример 15.1. Вычислить работу, которая производится при равномерном подъеме груза G= 200 Н по наклонной плоскости на расстояние s = 6 м, если угол, образуемый плоскостью с горизонтом, =30°, а коэффициент трения скольжения равен f = 0,01 (рис. 15.4).

Решение. Разложим силу тяжести G груза на две взаимно перпендикулярные составляющие G₁ и G₂— соответственно параллельную и перпендикулярную наклонной плоскости. Согласно второму закону трения скольжения, сила трения F_тр равна

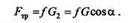
Применив теорему о работе равнодействующей, вычислим искомую работу как сумму работ сил сопротивления (работа силы G₂ и нормальной реакции Nравна нулю, так как эти силы перпендикулярны направлению перемещения s):

Подставив числовые значения, получим

Теорема о работе силы тяжести

Теорема. Работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.

Пусть материальная точка М движется под действием одной лишь силы тяжести G и за какой-то промежуток времени перемещается из положения М₁в положение М₂, пройдя путь s (рис. 15.5).

На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна. Из заштрихованного треугольника получим, что

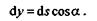
Элементарная работа силы G на пути ds

равна

Полная работа на пути s равна

Итак,

теорема доказана.

143

Силы, работа которых не зависит от вида траектории, называются потенциальными. К числу таких сил относятся, например, силы тяжести, силы всемирного тяготения, натяжение пружины.

Пример 15.2. Однородный массив ABCD массой т = 4080 кг имеет размеры, указанные на рис 15.6. Определить работу, которую необходимо затратить на опрокидывание массива вокруг ребра D.

Решение. Определим силу тяжести G массива:

G = mg = 4080 9,81 = 40 10³ Н = 40 кН.

Работа, которую необходимо затратить на опрокидывание массива, равна работе силы сопротивления, т. е. силы тяжести. Для того чтобы опрокинуть массив, необходимо его центр тяжести О (находящийся в геометрическом центре, так как массив однородный) перевести в положение O₁, после чего массив продолжит опрокидываться под действием силы тяжести, которая превратится из силы сопротивления в движущую силу.

Искомую работу определим, применив теорему о работе силы тяжести:

Работа постоянной силы,

Дата добавления: 2018-04-15; просмотров: 2642; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 31 32 33 34 353637 38 39 40 Следующая ⇒

Мы поможем в написании ваших работ!