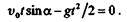Брошенной под углом к горизонту

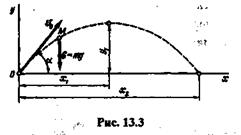
Рассмотрим материальную точку М массой т,брошенную из точки О поверхности Земли с начальной скоростью ₀под углом а к горизонту (рис. 13.3).

Определим движение точки М, считая, что на нее действует только сила тяжести G (сопротивлением воздуха пренебрегаем). Возьмем начало координат в точке О,ось х направим по горизонтали вправо, а ось у — по вертикали вверх. Составим дифференциальные уравнения движения точки:

 

Сокращая равенства на т,получаем:

 

Интегрируя уравнение (13.4), находим

 

По теореме о проекции скорости на координатную ось

 

Следовательно, проекция ско­рости точки М на ось х все время остается величиной по­стоянной, равной

130

Из последних двух равенств имеем

Интегрируя это уравнение, получаем

 

По условию при t = 0 х = 0, следовательно, произвольная постоян­ная

С₂ = 0.

Окончательно

Интегрируя уравнение (13.5), находим

 

Подставив в это уравнение значение t= 0, найдем произвольную по­стоянную

Следовательно,

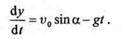
Интегрируя еще раз, получаем

По условию при t = 0 у = 0,следовательно, произвольная постоян­ная

С₄ = 0.

Окончательно

Таким образом, материальная точка М,брошенная со скоростью ₀ под углом к горизонту, движется согласно уравнениям

 

Для определения траектории точки М исключаем из полученных уравнений движения время. Определим время из первого уравнения дви­жения

и подставим его выражение во второе уравнение, в результате чего полу­чим уравнение траектории

131

 

Траектория точки М представляет собой параболу с вертикальной осью симметрии.

Определим время полета точки М,для чего во второе уравнение движения подставим значение y= 0. Тогда это уравнение примет вид

 

Отсюда находим два значения времени, при которых ордината равна нулю:

Первое значение времени соответствует началу полета, второе — его концу. Продолжительность полета

 

Определим дальность полета, для чего в первое уравнение движения подставим значение времени t₂:

или

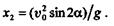
Из этого уравнения видно, что максимальная дальность полета х_mах имеет место при sin 2 = 1, т. е. при = 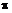/4 рад:

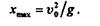
Определим наибольшую высоту подъема точки М,т. е. в тот момент, когда проекция ее скорости на ось ординат окажется равной нулю:

Из равенства определим t₁:

Следовательно, наибольший подъем точки имеет место в середине пути полета, т. е. при

Подставив значение t₁во второе уравнение движения, получим

откуда

132

Из этого уравнения видно, что максимальной высоты точка достига­ет при sin  = 1 или при  = 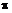/2 рад, т. е. когда точка брошена верти­кально вверх:

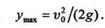
Пример 13.5. При аварии обод маховика паровой машины разорвался на не­сколько частей, которые отлетели от места аварии на разные расстояния, остава­ясь в плоскости вращения маховика. Наибольшее расстояние, на которое отлете­ли найденные куски, оказалось равным 280 м. Диаметр маховика D = 3,5 м. Опре­делить угловую скорость маховика в момент разрыва.

Решение. При рассмотрении вопроса о движении тела, брошенного под уг­лом к горизонту, была получена формула, определяющая максимальную даль­ность полета:

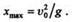
Из этой формулы определим окружную скорость маховика в момент разрыва:

 

При диаметре маховика D = 3,5 м его угловая скорость в момент разрыва была равна

Следует заметить, что в действительности угловая скорость маховика в мо­мент разрыва была несколько больше, потому что в расчетах сопротивлением воздуха пренебрегали.

Глава 14

ОСНОВЫ КИНЕТОСТАТИКИ

Метод кинетостатики

Представим себе материальную точку массой т, движущуюся с ус­корением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F.

Воспользуемся одной из известных нам формул (основным уравне­нием динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики):

Перепишем это уравнение в следующем виде:

133

Выражение, стоящее в скобках, обозначается F^ин и называется си­лой инерции:

 

Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению. Тогда

 

Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717—1783), мож­но рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением рав­новесия, в действительности является видоизмененным уравнением дви­жения материальной точки.

Следует отметить, что до Даламбера над общим методом, с помо­щью которого уравнениям динамики придается форма уравнений стати­ки, работали члены Петербургской Академии наук Я. Герман (1716) и Л. Эйлер (1737).

Принцип Даламбераформулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.

Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направле­нию неизменной, в результате чего оно будет действовать на связь, вызы­вающую ускорение, с силой, равной силе инерции. В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет уско­рение, а соседние частицы являются для нее связями. Поясним это на примере (рис. 14.1). Пусть к телу, лежащему на горизонтальной плоскости, привязана нить, способная выдерживать силу тя­жести G этого тела. Если к нити приложить силу R статически (постепенно), то тело будет поднято вверх и нить не оборвется; если силу R приложить динамически (внезапно, рывком), то нить оборвет­ся. Это явление объясняется следующим образом.

    Чтобы поднять груз, нужно сообщить ему ка­кое-то ускорение а. Для определения величины

 

 

134

натяжения нити применим принцип Даламбера и составим уравнение равновесия:

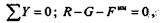
откуда

 

В первом случае грузу сообщается небольшое ускорение и сила инерции, увеличивающая натяжение нити, невелика; во втором случае ускорение, сообщаемое телу, значительное и сила инерции соответствен­но возрастает. В обоих случаях сила инерции не увеличивает давление на опору, так как приложена к телу условно.

Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора непод­вижны, то вес тела равен его силе тяжести.

Пример 14.1. В поднимающейся кабине лифта взвешивается тело на пру­жинных весах (сипа тяжести тела G = 50 Н), натяжение R пружины весов (т. е. вес тела) равно 51 Н. Найти ускорение кабины.

Решение. Применим к телу принцип освобождаемое, отбросим пружинные весы и заменим их реакцией R, равной натяжению пружины.

Для решения задачи применим метод кинетостатики, т. е. приложим к телу силу инерции F^ин. Составим уравнение равновесия взвешиваемого тела, спроеци­ровав все силы на вертикальную ось у; предполагаем, что ускорение а кабины направлено вверх и, следовательно, сила инерции направлена вниз (расположение векторов сил см. на рис. 14.1):

Модуль силы инерции определяем по формуле

Подставив это выражение в уравнение, определим ускорение

Ускорение получилось положительным, следовательно, как и предполага­лось, оно направлено вверх.

---

Дата добавления: 2018-04-15; просмотров: 817; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!