Отже, одна проекція об'єкту не дозволяє судити про його форму і розміри, тобто однопроекційне креслення є необоротним.

Паралельне проекціювання

Якщо за центр проекцій прийняти невласну точку S простору, то проекціювальні прямі АА₁, ВВ₁, будуть паралельними між собою. Для їх побудови замість відсутньої на кресленні точки S задають напрям проекціювання s (рис. 1.4).

Рис. 1.4

Такий вид проекціювання називається паралельним, а точки А₁, В₁, D₁ перетину проектуючих прямих з площиною проекцій П₁ – паралельними проекціями точок А, В, D, простору. Очевидно, що при паралельному проектуванні, як і при центральному, кожна точка простору має на площині П₁ одну проекцію. Ця проекція не визначає положення точки в просторі.

Інваріанти паралельного проекціювання

1. Проекція точки на площину є точка (рис. 1.4)

A ·A₁.

2. Проекція прямої в загальному випадку пряма: І  І₁, (рис. 1.5); вона вироджується в точку, якщо пряма паралельна до напряму проекціювання.

Рис. 1.5

3. Якщо точка належить лінії, то проекція точки належить проекції лінії (рис. 1.6).

A Î І A₁ Î І₁

Рис. 1.6

Наслідки з п.п. 2 та 3. Для побудови проекції прямої досить побудувати проекції двох точок, що належать прямій:

A Î І ^ B Î І =A₁ Î І₁ ^ B₁ Î І₁

4. Точка перетину ліній проектується в точку перетину їх проекцій (рис. 1.5):

К = а ⊓ b K₁ = а₁ ⊓ b₁.

5. Проекції паралельних прямих паралельні (рис. 1.6):

І // І' =І₁ // І₁'

Наслідки:

1) відношення довжин відрізків паралельних прямих рівне відношенню довжин їх проекцій (рис. 1.6):

[АВ] // [CD] ]

Якщо точка, що належить відрізку прямої, ділить його в деякому відношенні, то проекція точки ділить проекцію відрізка в тому ж відношенні (рис. 1.6).

6. Якщо геометрична фігура Ф належить площині Σ, паралельній площині проекцій (наприклад, П₁), то проекція цієї фігури на площину П₁ конгруентна самій фігурі. Наприклад, якщо відрізок МN паралельний площині проекцій, то його проекція на дану площину конгруентна самому відрізку (рис. 1.6).

7. Проекція геометричної фігури не змінюється при паралельному перенесенні площини проекцій.

Ортогональне проекціювання

Якщо напрям проекціювання перпендикулярний площині проекцій, паралельне проекціювання називається ортогональним (прямокутним):

s ^ П₁  (AA₁) ^ П₁.

В цьому випадку проекція А₁ точки А називається ортогональною, або прямокутною (рис. 1.7). Інакше проекціювання називається косокутним.

Рис. 1.7

Рис. 1.8

Ортогональне проекціювання, будучи окремим випадком паралельного, значно спрощує побудову проекцій геометричних фігур і є основним при виконанні комплексних креслень технічних форм (рис. 1.8). Розглянуті в попередніх параграфах однопроекційні креслення геометричних фігур є необоротними. За ними не можна в думках відтворити просторову форму і розміри зображеного об'єкту. Існують різні способи усунення цього недоліку однопроекційних креслень залежно від прийнятого виду проекціювання.

Наприклад, при центральному проекціюванні точку можна проектувати з двох різних центрів (рис. 1.9), при паралельному – за допомогою двох різних напрямів, при ортогональному – на дві пересічні площини. Неважко відмітити, що в кожному з цих випадків виходять дві проекції А₁, та А'₁, точки А, що однозначно визначають її положення в просторі.

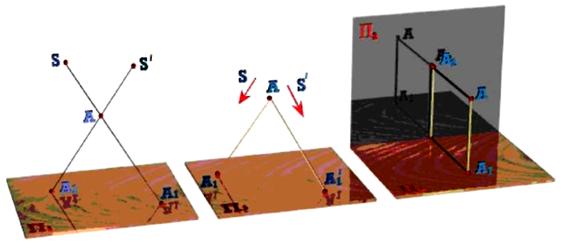
Рис. 1.9

ЛЕКЦІЯ №·2. КОМПЛЕКСНІ КРЕСЛЕННЯ ГЕОМЕТРИЧНИХ ФІГУР

2.1. Комплексне креслення точки.

2.2. Комплексні креслення ліній.

2.3. Комплексні креслення прямих ліній.

Рис. 2.1

Комплексне креслення точки

Розглянемо систему двох взаємно перпендикулярних площин П₁ та П₂ (рис. 2.1). Площину П₁ розташуємо горизонтально і назвемо горизонтальною площиною проекцій, а площину П₂, перпендикулярну П₁, розташуємо прямо перед собою і назвемо фронтальною площиною проекцій. Лінія х₁₂ їх перетину називається віссю проекцій.

Візьмемо будь-яку точку А (рис. 2.1) і побудуємо її ортогональні проекції А₁ та А₂ відповідно на площинах П₁ та П₂. Точка А₁ називається горизонтальною проекцією точки А, а точка А₂ – її фронтальною проекцією.Точка А та її ортогональні проекції А₁ та А₂ належать одній площині. [(АА₁)⊓(АА₂)], є перпендикулярною П₁, П₂ та осі х₁₂. Відстань |АА₁| точки А до площини П₁ називається висотою точки А, а її відстань |АА₂| до площини П₂ – глибиною точки А.

Просторова модель площин проекцій (рис. 2.1) незручна для практичного використання, оскільки на площині П₁ відбувається спотворення форми і розмірів горизонтальної проекції геометричної фігури. Для того, щоб перейти від просторової моделі площин проекцій до більш простої площинної моделі, тобто до плоского креслення, сумістимо площину П₁ з площиною П₂, обертаючи її навколо осі х₁₂ в напрямі, вказаному на рис. 2.1 стрілками. В результаті отримаємо комплексне креслення точки А, яке складається з комплексу двох її проекцій А₁ та А₂, що належать одній прямій, перпендикулярній осі х₁₂ (рис. 2.1). Пряма (А₁,А₂) та х₁₂, що сполучає дві проекції точки на комплексному кресленні, називається лінією зв'язку. Отримане таким чином комплексне креслення точки буде оборотним, оскільки дві її проекції А₁ та А₂ однозначно визначають положення точки А в просторі.

У технічній практиці для визначення форми та розмірів предмету застосовується принцип внутрішнього координування, при якому задаються розміри предмету, що характеризують форму і взаємне розташування його точок, ліній і поверхонь щодо його конструкторських і технологічних баз, а не щодо площин проекцій. Тому в техніці прийнятий безосний спосіб виконання креслень. Площини проекцій при цьому в просторі не фіксуються, вісь проекцій стає невизначеною і на кресленні не наноситься (рис. 2.2,в). Підставою для цього є те, що проекція геометричної фігури не змінюється при паралельному перенесенні площини проекцій (п.7, розділ 1.3, лекція №·1).

Лінія зв'язку [А₁А₂] на безосному комплексному кресленні проводиться вертикально. Якщо з яких-небудь причин необхідно зафіксувати площини проекцій П₁ та П₂, то на безосному комплексному кресленні наноситься вісь проекцій х₁₂ перпендикулярно лініям зв'язку в будь-якому зручному місці між горизонтальною і фронтальною проекціями геометричної фігури.

У багатьох випадках для виявлення форми і розмірів предмету доводиться будувати його проекції не на дві, а на більшу кількість площин. Значна частина предметів вимагає побудови трьох проекцій. Для побудови третьої проекції предмету застосовується профільна площина проекцій П₃, перпендикулярна П₁ та П₂ (рис. 2.2).

Рис. 2.2

Ортогональна проекція А₃ точки А на профільну площину проекцій називається профільною проекцією точки. Відстань /АА₃/ точки А до площини П₃ називається широтою точки А. Очевидно, що дві будь-які проекції точки А визначають її положення в просторі (рис. 2.2). Утворення комплексного креслення точки А (рис. 2.2,б) зрозуміло з просторового креслення.

За двома заданими проекціями точки можна побудувати її третю проекцію, користуючись умовами зв'язку між проекціями точки на комплексному кресленні (рис. 2.2,б):

· горизонтальна і фронтальна проекції точки належать одній вертикальній лінії зв'язку;

· фронтальна і профільна проекції точки належать одній горизонтальній лінії зв'язку;

· горизонтальна і профільна проекції точки належать ламаній лінії зв'язку, вершина якого належить постійній прямій k креслення (пряма k є бісектрисою прямого кута, утвореного ламаною лінією зв'язку).

На безосному комплексному кресленні умови зв'язку між проекціями точки зберігаються (рис. 2.2,в). Якщо задана система взаємозв'язаних точок А,В,С, то за двома проекціями кожної з точок можна побудувати третю, якщо на ній є три проекції однієї з точок, наприклад точки А (рис. 2.3,а). Точка А називається при цьому базовою.

Рис. 2.3

Якщо прийняти площини проекцій П₁, П₂ та П₃ за координатні площини декартової системи координат, то довжини відрізків, що виражають відстані точки А до площини проекцій, віднесені до одиниці довжини /е/ будуть координатами точки А (рис. 2.2,а,б):

|AA₃| / |e| = x – абсциса (широта);

|A₂| / |e| = у – ордината (глибина);

|A₁| / |e| = z – апліката (висота).

У технічних кресленнях за одиницю довжини приймають |е| = 1·мм. За координатами точки А(х,у,z) можна побудувати її проекції, а за заданими проекціями визначити її координати (рис. 2.2,б). При безосному способі зображення координати точки стають невизначеними. В цьому випадку для побудови комплексного креслення точки можна скористатися різницями координат, які не залежать від положення площин проекцій (рис. 2.3,б), або побудувати на ньому проекції координатних осей і віднести точку до системи координат Охуz (рис. 2.3,в).

Висновки

1.Сукупність двох і більше взаємозв'язаних ортогональних проекцій геометричної фігури, розташованих на одній площині креслення, називається комплексним кресленням.

2.Оборотне комплексне креслення повинне містити не менше двох проекцій геометричної фігури.

3. Для того, щоб креслення геометричної фігури було оборотним, воно повинно містити стільки проекцій, щоб кожна її точка мала не менше двох проекцій.

Комплексні креслення ліній

Лінії серед геометричних фігур займають особливе положення. Крім службового застосування, при виконанні зображень і різних графічних побудов, вони дають можливість вирішувати багато наукових та інженерних задач. Наприклад, за допомогою ліній можна створити наочні моделі багатьох процесів, встановити і досліджувати функціональну залежність між різними параметрами, конструювати поверхні технічних форм і т.п. Лінію можна представити або як межу поверхні, або як слід безперервно рухомої в просторі точки. Оскільки положення точки на лінії визначається однією безперервно змінною величиною (одним параметром), лінія є однопараметричною (одновимірною) безперервною безліччю точок. Для нарисної геометрії другий, так званий кінематичний, спосіб представлення лінії є зручнішим. Існують прямі, ламані та криві лінії.

Дата добавления: 2018-04-15; просмотров: 123; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!