Б). Знаки, що позначають відносини між геометричними фігурами
// – паралельність двох геометричних фігур,
^ – перпендикулярність,
_ –прямі, що схрещуються,
⊓– перетин геометричних фігур (множин),
= – рівні, співпадають або результат перетину геометричних фігур,
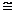– конгруентність.
В). Знаки, що позначають геометричні перетворення
– відображається.
Г). Знаки, що позначають множини, операції над ними і відношення між множинами
А, В, С,... – множини.
Ф – порожня множина.
а, b, с,... – елементи множини.
{...} – складається з, наприклад: М={а, b, с} – безліч М, що складається з елементів а, b, с (і лише з них). М={а:Р(а)} – множина, що складається з таких а, які володіють властивістю Р, наприклад: М={N:(/0N/=R)} – М є безліч таких точок N, відстань яких до точки О рівна R (коло на площині або сфера у просторі).
Ζ приналежність, наприклад:
а) А Î l – точка А належить прямій 1,
б) b 'М– пряма b проходить через точку М або пряма b містить точку М,
в) Ï –не належить.
þ – включення (є частиною, підмножиною, міститься в., включає, містить в собі), наприклад:
а) а þ Г – пряма а належить площині Г (розуміється в сенсі: безліч точок прямої а є підмножина безлічі всіх точок площини Г),
б) Гבа –площина Г проходить через пряму а або площина Г містить пряму а.
⊔ – об'єднання множин, наприклад:
АВСD = [АВ] ⊔[ВС] ⊔[СD] – ламана лінія є об'єднання відрізків.
⊓ – перетин множин, наприклад: b = Δ⊓Г – пряма b є перетин Δ і Г.
|
|
|
І ⊓ m = Ф – перетином прямих є порожня множина, тобто прямі паралельні або схрещуються.
Д. Знаки, що позначають логічні операції
^ – відповідає кон’юнкції "І".
n – відповідає диз’юнкції "АБО".
] – логічне проходження, означає "якщо ..., то"
ó – в тому і лише в тому випадку, якщо....
ЛЕКЦІЯ №·1. МЕТОДИ ПРОЕКЦІЮВАННЯ
1.1. Центральне проекціювання.
1.2. Паралельне проекціювання.
1.3. Інваріанти паралельного проекціювання.
1.4. Ортогональне проекціювання.
Центральне проекціювання. Поняття про проекційний простір
Для того, щоб побудувати проекцію, наприклад, деякої точки А, вибирається довільна площина П', звана площиною проекцій, і точка S, що не належить площині П', звана центром проекцій (рис. 1.1).
Рис. 1.1
Операція проекціювання полягає в тому, що через точки S та А проводиться пряма до перетину з площиною П'.
Пряма SА називається проекціювальною прямою, а точка А' перетину проекціювальної прямої з площиною проекцій П', – центральною проекцією точки А на площині П' (рис. 1.1). Можна побудувати центральні проекції інших точок простору (В,С,D...), за винятком тих, які належать площині П, що проходить через центр проекцій S і паралельна П'. В цьому випадку проекціювальні прямі виявляються паралельними площині П', і точок перетину їх з площиною в звичайному сенсі немає. Цей недолік центрального проекціювання усувається доповненням евклідова простору так званими нескінченно віддаленими або невласними елементами.
|
|
|
Доповнення евклідова простору невласними елементами дозволяє ліквідовувати виключення в основних положеннях елементарної геометрії та стверджувати:
· кожні дві прямі, що належать одній площині, завжди перетинаються (у власній або невласній точках);
· дві будь-які площини простору завжди перетинаються (лінія перетину – власна або невласна пряма);
· пряма і площина завжди перетинаються (у власній або невласній точках), отже, проекцією точки С, що належить площині П та П' буде невласна точка С'.
Описаним методом центрального проекціювання може бути побудована проекція будь-якої точки геометричної фігури, а отже, і проекція самої фігури. Наприклад, центральною проекцією відрізка [ВС] на площині П' є безліч центральних проекцій усіх точок відрізка [ВС] – [В'С'] (рис. 1.2).
Рис. 1.2
При центральному проекціюванні відбувається спотворення форми, розмірів та деяких інших властивостей предмету (рис. 1.3). Разом з тим, неважко відмітити, що частина властивостей зберігається, наприклад, проекція точки є точка; проекція прямої – теж пряма лінія. Якщо точка належить прямій, то проекція точки належить проекції тієї ж прямої; точка перетину прямих проектується в точку перетину їх проекцій. Проекція предмету, побудована методом центрального проекціювання, називається перспективою (рис. 1.3).
|
|
|
Рис. 1.3
Побудова проекцій паралельно об'єкту називається прямим завданням нарисної геометрії. Неважко відмітити, що метод центрального проекціювання дозволяє вирішувати її однозначно: кожна точка має на площині П' єдину проекцію, оскільки проекціювальна пряма перетинається з площиною П' в одній точці. Так, точка А (рис.1.1) має на площині П' єдину проекцію А', відрізок [ВС] – єдину проекцію [В'С'], будь-яка геометрична фігура – єдину проекцію.
У практичній діяльності необхідно вміти не тільки створювати креслення, але і читати їх, тобто судити за кресленням однозначно про сам предмет. Визначення форми і розмірів об'єкту за його кресленням називається зворотним завданням нарисної геометрії. Одна проекція точки не визначає її положення в просторі, оскільки може бути проекцією будь-якої точки, належної проекціювальній прямій. Так, точка А' (рис. 1.1) може бути проекцією будь-якої точки, що належить прямій SА; [В'С'] на рис. 1.2 – проекцією будь-якої лінії, що належить проекціювальній площині, що визначається точкою S і прямою ВС.
|
|
|
Дата добавления: 2018-04-15; просмотров: 220; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!