Основна теорема аксонометрії (теорема ПОЛЬКЕ)
Розглянувши загальні відомості про аксонометричні проекції, можна зробити такі висновки:
· аксонометричні креслення оборотні;
· аксонометрична і вторинна проекції точки цілком визначають її положення в просторі.
Аксонометричні проекції оборотні, якщо відома аксонометрія трьох головних напрямів вимірювань фігури і коефіцієнти спотворення на цих напрямах. Аксонометричні проекції фігури є її проекціями на площині довільного положення при довільно вибраному напрямі проекціювання. Очевидно, можливо і зворотнє. На площині можна вибрати довільне положення осей з довільними аксонометричними масштабами.
У просторі завжди можливе таке положення натуральної системи прямокутних координат і такий розмір натурального масштабу по осях, паралельною проекцією яких є дана аксонометрична система.
Німецький вчений Карл Польке (1810 – 1876) сформулював основну теорему аксонометрії: три відрізки довільної довжини, що лежать в одній площині і виходять з однієї точки під довільними кутами, представляють паралельну проекцію трьох рівних і взаємно перпендикулярних відрізків, що виходять із однієї точки в просторі.
Згідно цієї теореми, будь-які три прямі в площині, що витікають з однієї точки і не співпадають між собою, можна прийняти за аксонометричні осі. Будь-які відрізки довільної довжини на цих прямих, відкладені від точки їх перетину, можна прийняти за аксонометричні масштаби. Ця система аксонометричних осей і масштабів є паралельною проекцією деякої прямокутної системи координатних осей і натуральних масштабів.
|
|
|
У практиці побудови аксонометричних зображень зазвичай застосовують лише деякі певні комбінації напрямів аксонометричних осей і аксонометричних масштабів: прямокутна ізометрія і диметрія, косокутна фронтальна диметрія, кабінетна проекція та ін.
Стандартні аксонометричні проекції
Згідно ДСТ 2.317-69, з прямокутних аксонометричних проекцій рекомендується застосовувати прямокутні ізометрію і диметрію. Між коефіцієнтами спотворення і кутом φ, створеним напрямом проекціювання і картинною площиною, існує така залежність:
u2+υ2+ω2=2+ctq2φ,
якщо φ=900, то u2+υ2+ω2=2,
В ізометрії u=υ=ω і, отже, 3u2=2, звідки u=  ≈ 0,82.
≈ 0,82.
Таким чином, у прямокутній ізометрії розміри предмету за всіма трьома вимірюваннями скорочуються на 18%. ДСТ рекомендує ізометричну проекцію будувати без скорочення по осях координат (рис. 5.2), що відповідає збільшенню зображення проти оригіналу в 1,22 рази.

Рис. 5.2
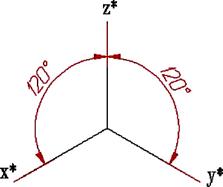
Рис. 5.3
При побудові прямокутної диметричної проекції скорочення довжин по осі у' (рис. 5.3) приймають удвічі більшим, ніж по двох інших, тобто вважають, що u=ω, а υ=0,5u. Тоді 2u2+(0,5u)2=2, звідки u2=8/9 і u ≈0,94, а υ=0,47. У практичних побудовах від таких дробних коефіцієнтів зазвичай відмовляються, вводячи масштаб збільшення, що визначений співвідношенням 1/0,94=1,06, і тоді коефіцієнти спотворення по осях x' і z' рівні одиниці, а по осі у' удвічі менші υ=0,5. З косокутних аксонометричних проекцій ДСТ- ом передбачено застосування фронтальної та горизонтальної ізометрії і фронтальної диметрії (останню ще називають кабінетною проекцією).
|
|
|
Коло в аксонометрії
При паралельному проекціюванні кола на будь-яку площину П* отримуємо її зображення в загальному випадку у вигляді еліпса (рис. 5.4).
t2 // CB; t4 // AD; t6 // CB; t8 // AD.

Рис. 5.4
Як би не була розташована площина кола, спочатку доцільно побудувати паралелограм A*B*C*D* – паралельну проекцію квадрата ABCD, описаного біля даного кола, а потім за допомогою восьми точок і восьми дотичних вписати в нього еліпс. Точки 1, 3, 5і 7 – середини сторін паралелограма. Точки 2, 4, 6 і 8 розташовані на діагоналях так, що кожна з них ділить напівдіагональ у співвідношенні 3:7. Дійсно, на основі властивостей паралельного проекціювания можна записати, що А2/1О=A*2*/2*O*, тобто А1/1О·=·(r √2-r)/r ≈3/7.
|
|
|
З восьми дотичних до еліпса перші чотири – це сторони паралелограма, а решта t2, t4, t6, t8 – прямі, паралельні його діагоналям. Так дотична t2* до еліпса паралельна діагоналі C*D*.

Рис. 5.5
Пояснюється це тим, що t2* і C*D* є проекціями двох паралельних прямих t2 і CD. Графічні побудови, що передують викреслюванню самого еліпса, доцільно виконувати в наступній послідовності (рис. 5.5):
1. Побудувати аксонометричну проекцію квадрата – паралелограм A*B*C*D* і провести діагоналі A*C* і B*D*;
2. Відзначити середини сторін паралелограма – точки 1*, 3*, 5* і 7* ;
3. На відрізку 3*B*, як на гіпотенузі, побудувати прямокутний рівнобедрений трикутник 3*KB*;
4. З точки 3* радіусом 3*K описати півколо, яке перетне A*B* в точках L і M; ці точки ділять відрізок 3*A* і рівний йому відрізок 3*B* у відношенні 3:7;
5. Через точки L і М провести прямі, паралельні бічним сторонам паралелограма, і відзначити точки 2*, 4*, 6* і 8*, розташовані на діагоналях;
6. Побудувати дотичні до еліпса в знайдених точках. Дотичні t2 і t6 паралельні BD, а дотичні t4 і t8 паралельні AC.
7. Отримавши вісім точок і стільки ж дотичних, можна з достатньою точністю накреслити еліпс.

Рис.5.6
|
|
|

Рис. 5.7
ДСТ 2.317-69 визначає положення кіл, що лежать у площинах, паралельних площинам проекцій для прямокутної ізометричної проекції (рис. 5.6) і для прямокутної диметрії (рис. 5.7).
Якщо ізометричну проекцію виконують без спотворення по осях x, у, z, то велика вісь еліпсів 1,2,3 рівна 1,22, а мала вісь – 0.71 діаметра кола.
Якщо ізометричну проекцію виконують із спотворенням по осях x, у, z, то велика вісь еліпсів 1, 2, 3 рівна діаметру кола, а мала – 0.58 діаметра кола.
Якщо диметричну проекцію виконують без спотворення по осях x і z, то велика вісь еліпсів 1, 2, 3 дорівнює 1,06 діаметра кола, а мала вісь еліпса 1 – 0.95, еліпсів 2 і 3 – 0.35 діаметра кола.
Якщо диметричну проекцію виконують із спотворенням по осях х і z, то велика вісь еліпсів 1, 2, 3 дорівнює діаметру кола, а мала вісь еліпса 1 – 0.9, еліпсів 2 і 3 – 0,33 діаметра кола.
1 – еліпс (велика вісь розташована під кутом 90О до осі у);
2 – еліпс (велика вісь розташована під кутом 90О до осі z);
3 – еліпс (велика вісь розташована під кутом 90О до осі х).
Дата добавления: 2018-04-15; просмотров: 191; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
