Основные предпосылки управления проектами 8 страница

Пример 26. Найдем вероятность выпадения двух единиц при двух бросаниях кубика.

Событие А – (при 1-м бросании выпала 1), событие В – (при 2-м бросании выпала 1). Тогда АВ –(оба раза выпала 1).

А и В – независимые события, так как результаты при втором бросании кубика не зависят от того, что выпало при первом бросании. Р(А)=Р(В)=1/6. Тогда Р(АВ)=Р(А)Р(В)=1/6х1/6=1/36.

Условная вероятность

Условной вероятностью Р(В|А) называется вероятность события В при условии, что событие А произошло. Тогда для зависимых событий Р(В|А) ≠ Р(В|Ā). Для независимых событий Р(В|А) = Р(В|Ā) = Р(В).

Пример 27. В примере 25 Р(В|А) = Р (2-й вынутый шар черный при условии, что 1-й вынутый шар черный) = Р(2-й вынутый шар черный | 1-й вынутый шар черный) = 11/19.

Р(В|Ā) = Р(2-й вынутый шар черный при условии, что1-й вынутый шар не черный) = Р(2-й вынутый шар черный | 1-й вынутый шар не черный) =12/19.

Поэтому события А и В зависимы.

Вероятность произведений зависимых событий

Теорема. Для зависимых событий А и В верно следующие: Р(АВ)=Р(А)Р(В|А)

Пример 28. Вернемся к примеру 25 и 27. Найдем вероятность того, что из урны вынуто два черных шара, то есть найдем вероятность события АВ. Р(из урны вынуты два черных шара)=Р(АВ)=Р(А)Р(В|А)=Р(1-й вынутый шар черный) х Р(2-й вынутый шар черный при условии, что первый вынутый шар черный) = 12/20х11/19 = 33/95.

Вероятность суммы двух совместных событий

Теорема. Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без учета вероятности произведения этих событий: Р(А+В)=Р(А)+Р(В)-Р(АВ).

Если события А и В несовместны, то АВ – невозможное событие. Тогда Р(АВ) = 0

Пример 29. Найдем вероятность выпадения хотя бы одной единицы при двух бросаниях кубика.

Событие А – (при первом бросании выпала 1), событие В –(при втором бросании выпало 1). Тогда А+В – (хотя бы раз выпало 1).

Р(А+В)=Р(А)+Р(В)-Р(АВ)=1/6+1/6-1/36=11/36

4.3. Дерево вероятностей

На практике часто возникают ситуации, когда требуется определить вероятность события, которое может произойти с одним из несовместных событий, образующих полную группу событий. Ответ дает так называемая формула полной вероятности. Но рассмотрим более простой и наглядный подход — дерево вероятностей.

Дерево вероятностей рисуют слева направо. Опыты обозначаются в виде кругов, а каждый исход — сплошной линией (ветвью), идущей от соответствующего круга. Около каждой ветви указывается вероятность соответствующего исхода. Сумма вероятностей на ветвях, выходящих из одного круга, равна единице. Двигаясь по ветвям и перемножая соответствующие вероятности, в конце пути получаем вероятность сложного события. Сложив нужные вероятности, найдем вероятность искомого события.

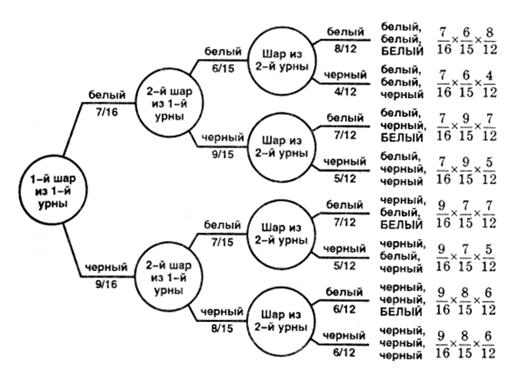
Пример 30. В 1-й урне находятся 7 белых и 9 черных шаров, во 2-й урне находятся 6 белых и 4 черных шаров. Из 1-й урны во 2-ю переложили 2 шара, а затем из 2-й урны извлекли один шар. Найдем вероятность того, что этот шар белый.

Провели три опыта:

1) извлекли из 1-й урны первый шар и переложили его во 2-ю урну;

2) извлекли из 1-й урны второй шар и переложили его во 2-ю урну;

3) из 2-й урны извлекли один шар.

Поэтому дерево вероятностей содержит три уровня вершин. Так как каждый раз возможны два исхода, то из каждой вершины выходят две ветви. Над каждой ветвью пишем название соответствующего исхода (белый или черный), а под ветвью — вероятность появления этого исхода.

Всего в нашем дереве 8 возможных путей:

1) белый, белый, белый;

2) белый, белый, черный;

...,

8) черный, черный, черный.

Это означает, что возможно 8 сложных событий.

Событие «белый, белый, белый» говорит о том, что оба переложенных шара из 1-й урны во 2-ю были белого цвета и что из 2-й урны извлекли белый шар. Вероятность того, что первый шар из 1-й урны был белым, равна 7/16 (всего 16 шаров, из них 7 белых). Вероятность того, что второй шар из 1-й урны был белым, равна 6/15 (всего осталось 15 шаров, но белых осталось 6). Вероятность того, что из 2-й урны извлекли белый шар, равна 8/12 (всего было 10 шаров (из них 6 белых), добавили 2 белых шара). Все вероятности изобразим под соответствующими линиями. Перемножив полученные числа 7/16x6/15x8/12, мы найдем вероятность появления события «белый, белый, белый».

Рисунок 4.1 – Дерево вероятности для решения примера 30.

Событие «черный, белый, белый» говорит о том, что сначала переложили из 1-й урны во 2-ю черный шар, затем белый и что из 2-й урны извлекли белый шар. Вероятность того, что первый шар из 1-й урны был черным, равна 9/16 (всего 16 шаров, из них 9 черных). Вероятность того, что второй шар из 1-й урны был белым, равна 7/15 (всего осталось 15 шаров, но белых по-прежнему 7). Вероятность того, что из 2-й урны извлекли белый шар, равна 7/12 (всего было 10 шаров (из них 6 белых), добавили черный и белый шары). Все вероятности изобразим под соответствующими линиями. Перемножив полученные числа 9/16x7/15x7/12, мы найдем вероятность появления события «черный, белый, белый». И т. д. Решение представлено на рисунке 4.1.

Нас интересует, когда шар из 2-й урны будет белым. Надо сложить вероятности тех событий, у которых на последнем месте написано «белый»: 7/16x6/15x8/12 + 7/16x9/15x7/12 + 9/16x7/15x7/12 + 9/16x8/15x6/12 = 55/96.

Пример 31. Предприятие рассматривает вопрос о выпуске нового товара на рынок. Вероятность успеха рекламной кампании оценивается в 0,8. В случае успешной рекламной кампании вероятность успешного выпуска нового товара на рынок составляет 0,6. В случае неудачи рекламной кампании вероятность успешного выпуска нового товара на рынок оценивается в 0,3. Определим вероятность успешного выпуска нового товара на рынок.

Мы провели два опыта:

1) провели рекламную кампанию;

2) выпустили товар на рынок.

Поэтому дерево вероятностей содержит два уровня вершин. Так как каждый раз возможны два исхода, то из каждой вершины выходят две ветви. Над каждой ветвью пишем название соответствующего исхода, а под ветвью — вероятность появления этого исхода (см. рисунок 4.2).

Рисунок 4.2 – Дерево вероятности для примера 31.

Нас интересует, когда выход товара на рынок будет успешным. Надо сложить вероятности тех событий, у которых на последнем месте написано «успешный»: 0,8x0,6 + 0,2x0,3 = 0,54.

Пример 32. По оценкам отдела маркетинга, вероятность роста объема продаж предприятия в ближайшее время равна 0,7. Из прошлого опыта известно, что положительные прогнозы отдела маркетинга сбываются в 85% случаях, а отрицательные — в 90% случаях. Определим вероятность роста объема продаж предприятия в ближайшее время.

Провели два опыта:

1) прогноз отдела маркетинга;

2) наблюдение за объемом продаж.

Рисунок 4.3 – Дерево вероятности для примера 32.

Нас интересует рост объема продаж на самом деле. Надо сложить вероятности тех событий, у которых на последнем месте написано «рост»: 0,7x0,85 + 0,3x0,1 = 0,625.

Формула Байеса

Часто, приступая к анализу вероятностей, имеем предварительные (априорные) значения вероятностей интересующих нас событий. Проведя опыт и применив формулу Байеса, получим новые (апостериорные) значения вероятностей.

Предположим, что возможно появление события А вместе с одним из событий, образующих полную группу событий (их называют гипотезами). Вероятности гипотез известны. Провели опыт, и произошло событие А. Как изменились вероятности гипотез? Строим дерево вероятностей и по нему находим ответ.

Пример 33. Производственная линия оснащена автоматикой для выявления бракованных деталей. Производитель утверждает, что доля бракованных деталей равна 3%. Если деталь бракованная, то автоматика определит ее как бракованную в 85% случаев. Автоматика определяет хорошие детали как бракованные в 5% случаев. Очередная деталь отнесена автоматикой к числу бракованных деталей. Определим вероятность того, что деталь действительно бракованная.

Два опыта:

1) тип детали (бракованная или годная);

2) автоматическая проверка детали.

Строим дерево вероятностей (рисунок 4.4).

Рисунок 4.4 – Дерево вероятности для примера 33.

Вероятность того, что деталь будет отнесена автоматикой к числу бракованных деталей, равна 0,97x0,05 + 0,03x0,85 = 0,074. Вероятность того, что бракованная деталь будет отнесена автоматикой к числу бракованных деталей, равна 0,03x0,85 = 0,0255.

Разделив второе из этих чисел на первое, получим ответ задачи: 0,0255/0,074 ≈ 0,345.

4.4. Повторение испытаний

Для повторения испытаний используют следующие теоремы:

Схема Бернулли. Производится серия из п независимых испытаний. В каждом из них вероятность появления события А постоянна и равна р. Вероятность появления события «не-А» = Ā (то есть вероятность не появления события А) равна q = 1 — р. Тогда вероятность того, что событие А появится ровно k раз, равна р_п(k) = C_n^kp^kqⁿ^-^k. где С = n! / (k!(n-k)! биномиальный коэффициент, n! = 1×2×...×n — факториал числа. Считается, что 0! = 1.

Локальная теорема Муавра-Лапласа. Если п велико, то используют вспомогательную величину и определяют искомую вероятность по формуле: , где , φ(-x) = φ(x). Значения функции φ(x) берутся из специальной таблицы. Можно также воспользоваться мастером функций f_x пакета Ехсеl : φ(x) = НОРМРАСП (х; 0; 1; 0).

Теорема Пуассона. Если вероятность р < 0,1, то формула Муавра-Лапласа непригодна. В этом случае применяют теорему Пуассона. Положим λ = пр. Тогда

Можно воспользоваться мастером функций f_x. пакета Ехсеl: = ПУАССОН (k; λ; 0) и р_п(k ≤ k₂) = ПУАССОН (k₂; λ; 1).

Интегральная теорема Лапласа. Если п велико, то вводят величины , и определяют вероятность по формуле:

P_n(k₁≤ k ≤ k₂) ≈ Ф(х₂)-Ф(х₁) где – функция Лапласа.

Значения функции Ф(х) берутся из специальной таблицы.

Важно, что Ф(-х) = -Ф(х)

Можно также воспользоваться мастером функций f_x.пакета Ехсеl: Ф(х) = НОРМРАСП(x; 0; 1; 1) – 0,5. Полагают Ф(х) = 0,5 при х > 5.

Относительная частота

Относительная частота события А (или просто частота) — это отношение числа опытов т, где появилось это событие, к общему числу опытов п: w(А) = т/п.

Пример 34. Произведено n = 100 выстрелов, зарегистрировано т = 80 попаданий. Событие А = {попадание в цель}. Тогда относительная частота события А равна w(А) = т/n = 80/100 = 0,8.

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях. Производится серия из п независимых испытаний. В каждом из них вероятность появления события А равна р, р — это теоретическая величина. На практике же мы наблюдаем для события А относительную частоту w(А) = т/п. Как сильно w(А) может отклониться от р?

Вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа ε > 0, можно найти: Р(|т/п — р| < ε) , где Ф(х) — это функция Лапласа.

4.5. Дискретные случайные величины

Случайная величина — это величина, которая в результате каждого опыта принимает одно заранее неизвестное значение, зависящее от случайных причин. Будем обозначать случайные величины латинскими буквами X, Y, Z,...

Среди случайных величин выделяют дискретные и непрерывные. Дискретная случайная величина — это случайная величина, которая может принимать не более чем счетное (то есть либо конечное, либо счетное (можно занумеровать) множество значений). Примеры дискретных случайных величин:

· число попаданий в мишень при п выстрелах (возможные значения от 0 до п);

· число выпавших гербов при п бросаниях монеты (возможные значения от 0 до n);

· число выпавших единиц при п бросаниях кубика (возможные значения от 0 до п);

· число прибывших самолетов в аэропорт (счетное множество значений);

· число поступивших вызовов на АТС (счетное множество значений).

Математическое ожидание дискретной случайной величины, его свойства.Математическое ожидание дискретной случайной величины X равно М(Х) = . В англоязычной литературе вместо М(Х) используют обозначение Е(Х).

Свойства математического ожидания М(Х):

1. М(Х) заключено между наименьшим и наибольшим значениями случайной величины X.

2. Если X = С = const (постоянная), то М(С) = С.

3. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С × М(Х).

4. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий М(Х + У) = М(Х) + М(Y).

5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий М(ХY) = М(Х)М(Y).

Распределение Пуассона.Если дискретная случайная величина X может принимать только целые неотрицательные значения с вероятностями
Р(Х = k) = λ^ke^-λ/k!, то говорят, что она распределена по закону Пуассона с параметром λ. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру λ.

Примеры случайных величин, имеющих распределение Пуассона: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в готовой продукции.

4.6. Непрерывные случайные величины

Непрерывная случайная величина — это случайная величина, значения которой целиком заполняют некоторый интервал. Время безотказной работы прибора, длина сделанной детали, процентная ставка дохода по инвестициям, отклонение точки падения снаряда от цели — все это примеры непрерывных случайных величин.

Функция распределения, ее свойства.Так как невозможно перебрать все значения непрерывной случайной величины, то ее задают с помощью функции распределения. Функцией распределения (интегральным законом распределения) случайной величины X называется функция F(х) = Р(Х < х), где Р(Х < х) — вероятность того, что случайная величина X примет значение, меньшее х. Свойства функции распределения:

1. 0 ≤ F(х) ≤ 1.

2. Вероятность того, что случайная величина X примет значения из интервала (α; β) равна разности значений функции распределения на концах этого интервала: Р(α < X < β) = F(β) - F(α).

3. F(х) — неубывающая функция.

4. , .

Плотность распределения вероятностей, ее свойства.

Функция f(х) = F'(х) называется плотностью распределения вероятностей (дифференциальной функцией). График Функции f(х) называется кривой распределения.

Свойства функции f(х):

1. 0 ≤ f(х).

2. .

3. Вероятность того, что случайная величина X примет значения из интервала (α; β), — это Р(α < X < β ) = 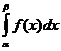. Геометрически это означает, что вероятность попадания случайной величины X в интервал (α; β) равна площади криволинейной трапеции, ограниченной функцией f(х), осью Ох и прямыми
х = α и х = β.

4. .

Контрольные вопросы к лекции 4:

1. Что изучает теория вероятности?

2. Что такое понятие опыт в теории вероятности?

3. Что является достоверным и невозможным событием?

4. Роль вероятности события для прогнозирования его появления?

5. Прогнозирование экономических показателей с помощью дерева вероятности.

6. В чем особенности прогнозирования при повторении испытаний?

7. Что такое относительная частота?

8. В чем отличие дискретных случайных величин от неприрывных?

9. Роль плотности распределения вероятностей?

Статистические методы прогнозирования и планирования

5.1. Проблема обоснованности и точности статистических оценок

Методы математической и прикладной статистики, в том числе корреляционный и регрессионный анализ, используются в прогнозировании развития экономических, производственных систем, рынков сбыта.

Вполне обоснованно предполагается, что все или некоторые данные содержат случайную составляющую. Результаты, получаемые при статистической обработке данных, могут различаться по степени точности и вероятностной обоснованности. Прогнозы могут основываться на статистических оценках, если эти оценки обоснованы, определена их вероятность и точность. Без такого обоснования прогнозы не заслуживают доверия.

Дата добавления: 2018-04-15; просмотров: 3048; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!