Лабораторная работа № 4(6 часов)
Оценка значимости коэффициентов регрессии.
На этом этапе статистического анализа проверяют случайно или значимо каждый коэффициент регрессии bj отличается от нуля.
Первое. Для оценки значимости коэффициентов вычисляют t- отношение.
(2.30)
где 
- среднее квадратичное отклонение коэффициента 
. определяется по закону накопления ошибок.
Отношение (2.30)можно вычислить и по формуле:
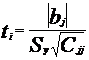(2.31)
Опишем процедуру определения величины 
.
Представим исходный статистический материал (см.табл. 2.1) в матричной форме. Для этого добавим в табл.2.1 столбец значений фиктивной переменной Xoi , равные 1 (т.е. Xo1 =1, Xo2 =1,… XoN =1). Тогда можно записать матрицу Х так:
(2.32)
Введем матрицу, транспонированную к Х
(2.33)
Перемножив матрицы ХТ и Х , получим:
(2.34)
Определитель матрицы (ХТХ) равен:
(2.35)
Алгебраические дополнения элементов матрицы (ХТХ) определяется так:
(2.36)
Вычисляются диагональные элементы 
матрицы, обратной матрице (ХТХ) :
(2.37)
Затем вычисляется t – отношение.
(2.38)
|
|
|
Второе.Проверяется условие:
(2.39)
где 
- табличное значение критерия Стьюдента для уровня значимости Р (обычно р=0.05);
f – число степеней свободы, равное числу степеней свободы дисперсии воспроизводимости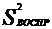 
.
Если условие (2.39) выполняется, то коэффициент считают статически значимым. Если условие (2.39) не выполняется, то коэффициент считают незначимым, т.е. равным нулю. Незначимые коэффициенты исключаются из уравнения регрессии (2.2), а оставшиеся пересчитываются заново.
Коэффициенты регрессии (2.2), определенные по данным пассивного эксперимента, взаимно связаны и нельзя проверить значимость каждого коэффициента в отдельности. Поэтому отношение (2.31) можно рассматривать как средство ранжировки факторов. После исключения из уравнения незначимых факторов, расчет повторяется. Окончательное исключение фактора из уравнения регрессии выполняется в случае, если остаточная дисперсия уменьшается.
ПРИМЕР:
Оценка значимости коэффициентов регрессии.
Запишем матрицу Х (2.32) соответственно таблице 3.1:
Транспонирование к Х матрица ХТ и имеет вид (2.33):
Перемножив матрицы ХТ и Х получим (2.33):
|
|
|
Алгебраические дополнения элементов матрицы (ХТ Х) определяется соответственно (2.36)
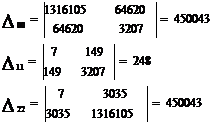
Вычисляем диагональные элементы 
(j=0,1,2)по формулам (2.37):
8,655; 
0,0048; 
0.029.
По формуле (2.31) рассчитываем t- отношение;
26,546; 
2,409; 
0,964.
Табличное значение критерия Стьюдента при уровне значимости F=0,05 и числе степеней свободы f=14;
Очевидно, что условие (2.39) 
выполняется только для отношения 
и 
. Таким образом, коэффициенты 
и 
значимые, коэффициент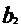 
незначимый. Незначимый коэффициент 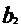необходимо исключить из уравнения регрессии (3.4), а оставшиеся коэффициенты пересчитать заново.
Прежде чем пересчитать коэффициенты уравнения, найдем остаточную дисперсию. Предположим, что все коэффициенты уравнения регрессии (3.4)значимые, тогда расчет а оставшиеся 
можно осуществить по формуле (2.40). значения 
уже определены (3.5). в результате получим (2.40):
=0,146. (3.7)
Число степеней свободы (2.40) f = 18.
Теперь из уравнения регрессии (3.4) исключаем коэффициент 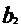, из таблицы 3.1 удаляем столбец значений Х2 и по оставшимся в таблице 3.1 данным рассчитываем коэффициенты и уравнения регрессии:
(3.8)
|
|
|
Коэффициенты уравнения (3.8) и определяются методом наименьших квадратов (2.14). Вывод расчетных формул для коэффициентов и описан в литературе /1,2,3/.
; (3.9)
(3.10)
по формулам (3.9), (3.10) и данным преобразованной таблицы 3.1 находим:
=-0,751; =371,87
уравнение регрессии (8.8) примет вид:
=371,87-0,751Х1 (3.11)
Подставляя в уравнение (3.11) значения Х1 из таблицы 3.1, находим 
для каждого опыта:
=39.93; 
=48,94; 
=47,44;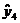 
=39.93;
=51,19; 
=47,44; 
=48,94. (3.12)
Используя полученные значения (3.12), данные таблицы 3.1 и формулу (2.40), вычисляем остаточную дисперсию для уравнения (3.11):
=3,632 (3.13)
Сравнивая значения (3.7) и (3.13) выясняем, что после исключения из уравнения (3.4) коэффициента 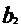остаточная дисперсия увеличилась значит, исключать этот коэффициент из уравнения регрессии (3.4) нельзя.
Таким образом, в качестве модели исследуемого процесса выбираем уравнение регрессии(3.4).
Дата добавления: 2018-04-05; просмотров: 213; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!