СТАТИСТИЧЕСКИЕ МОДЕЛИ ПРОЦЕССОВ  НА ОСНОВЕ  

ПАССИВНОГО ЭКСПЕРИМЕНТА

 

     При выявлении и описании зависимостей между случайными величинами по данным пассивного эксперимента применяют методы корреляционного и регрессивного анализов. Между случайными величинами может существовать, так называемая, корреляционная связь, при которой с изменением одной величины изменяется распределение другой. Для характеристики формы связи при изучении корреляционной зависимости пользуются управлением регрессии.

 

Лабораторная работа №1  (6 часов)

Определение коэффициентов уравнения множественной регрессии.

 

     Уравнение множественной регрессии, полученное по данным пассивного эксперимента, чаще всего записывается в виде линейного полинома:

;                     2.1

где b₀ – выборочный коэффициент, который называется свободным членом уравнения;

b_j-  выборочные коэффициенты, называемые линейными эффектами;

x_j– входные измеряемые и регулируемые параметры технологического процесса (факторы);

y^{^}– оценка выходного измеряемого параметра процесса;

к – число факторов.

     В реальном технологическом процессе всегда существуют неуправляемые и неконтролируемые параметры и изменение величины выходного параметра у носит случайный характер. Поэтому при обработке экспериментальных данных получают выборочные коэффициенты b₀ b_j  являющиеся оценками теоретических коэффициентов . Уравнение (2.1.) применяется для построения статистических моделей статики процессов химической технологии. Такая модель не несет необходимой информации о механизме процесса, его физико-химических свойствах. Однако уравнение регрессии может быть использовано для определения оптимальных условий протекания процессов, оптимальных составов приготовления смесей и т.п.

     Предположим, что проведен пассивный эксперимент и полученные данные сведены в таблицу 2.1.

Таблица 2.1

№ опыта	Факторы		Выходной параметр (параллельные опыты)
	X1	X2	y1	……	yu	………..	ym
1	X11	X21	Y11	……	Y1u	……	Y1m
2	X12	X22	Y21	……	Y2u	……	Y2m
…..	……	……	……	……	…..	……	……
i	X1i	X2i	Yi1	……	Yiu	……	Yim
……..	……	……	……	……	……	……	……
N	X1N	X2N	yN1	……	YNu	……	Ynm

 

Здесь число N - число опытов параллельных опытов. Требуется определить математическую модель в виде линейного полинома для некоторого процесса, имеющего входные параметры X₁ X₂ и выходной параметр y .

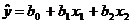
                       (2.2.)

и выполнить корреляционный и регрессионный анализ.

     Приведем схему корреляционного и регрессивного анализа по экспериментальным данным, когда каждый из N опытов повторен m раз. (табл. 2.1.)

     В каждой строчке табл. 2.1 находится среднее значение величины по m параллельным опытам;

i=1,2,……N                              (2.3)

Затем вычисляется среднее значение выходного параметра по N опытам.

                                                 (2.4)

и среднее значение факторов

        j = 1,2,…k                   (2.5)

находятся средние квадратические отклонения у х_j соответственно Sy Sx_j

                                           (2.6)

j= 1,2….k;                         (2.7)

Для уменьшения трудностей, связанных с расчетом коэффициентов уравнения регрессии перейдем от натурального масштаба к новому, проведя нормировку всех значений по формулам:

                                       (2.8)

I= 1,2,…N.                                                  (2.9)

Где У^о_i X_ji^o -нормированные значения выходной величины и факторов. Результаты нормировки всех значений сводятся в табл. 2.2

Таблица 2.2

№ опыта	Факторы		Входной параметр
	X1o	X2o	Уоi
1	X11o	X21o	Уо1
2	X12o	X22o	Уо2
..	…	…	…
I	X1io	X2io	Уоi
….	….	…	…
N	X1No	X2No	УоN

В новом масштабе:

(2.10)

выборочные коэффициенты корреляции рассчитываются так:

                              (2.11)

выборочные коэффициенты корреляции, вычисленные по формулам (2.11) равны коэффициентам корреляции между переменными, выраженными в натуральном масштабе, т.е.

                                                   (2.12)

     Доказано в математической статистике, что уравнение регрессии между нормированными переменными не имеет свободного члена:

                                                                           (2.13)

Коэффициенты уравнения (2.13) а₁ и а₂ определяется методом наименьших квадратов.

                                                          (2.14)

или

                                          (2.15)

Процедура нахождения коэффициентов а₁ и а₂ с сводится к задаче определения минимума функции Ф(а_1,а₂) . Необходимым условием минимума функции Ф(а_1,а₂) является.

                                                                               (2.16)

Продифференцировав выражение (2.15) получим:

                                            (2.17)

систему уравнений (2.17) можно записать так:

                                           (2.18)

Перейдем к системе нормальных уравнений:

                                                (2.19)

Уложим левую и правую части системы (2.19) на I(V-I). В первом уравнении получим следующие выражения при а₁ и а₂ (сравните выражения (2.10) и (2.11)).

                                   (2.20)

                                   (2.21)

Известно:

Учитывая выражения (2.20),(2.21) и (2.12), получим систему нормальных уравнений в виде:

                                                                         (2.22)

Решив систему уравнений (2.22) находим коэффициенты а₁ а₂ . Значения , рассчитывают по формулам (2.11), используя данные таблицы 2.2 .

Пример:

Таблица 3.1

№ опыта	ФАКТОРЫ		Значения У в параллельных опытах
	Х1	Х2	У1	У2	У3
1	442	23	41	42,54	39,35
2	430	21	47,51	49,5	51,36
3	432	16	44,97	41,59	43,2
4	442	22	41,52	39	38,4
5	427	22	51,7	49,76	53,8
6	432	22	46,76	48,6	50,55
7	430	23	52,44	48,5	50,4

     По результатам пассивного эксперимента (табл. 3.1) необходимо:

1. Найти математическую модель процесса в виде уравнения регрессии: 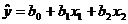                                                                                                 (3.1)

2. Провести корреляционный и регрессионный анализ.

3. Используя полученную адекватную модель процесса, определить:

А. Направление изменения значений факторов, увеличивающее выход продукта;

Б. Максимальный выход продукта в исследуемой области изменения факторов.

     Решение:

     По формуле (2.3) для каждой строки табл. 3.1 находится среднее значение  по трем (m=3) параллельным опытам.

40,963; 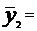             49,457;  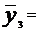 43,253;              39,64;

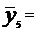51,753;              48,637;              50,447;              (3.2)

среднее значение выходного параметра и факторов  по 7 опытам вычисляются по формулам (2.4),(2.5):

среднее квадратичное отклонения  (формулы (2.6), (2.7)

 

выполним нормировку всех значений по формулам (2.8),(2.9) и результаты запишем в табл. 3.2.

таблица 3.2

№ опыта
1	1.406	0.704	-1.09
2	-0.595	-0.119	0.642
3	-0.262	-2.177	-0.623
4	1.406	0.292	1.359
5	-1.096	0.292	1.108
6	-0.262	0.292	0.475
7	-0.595	0.704	0.843

В новом масштабе соответственно выражениям (2.10)

Выборочные коэффициенты корреляции рассчитываем по формулам(2.11).

Известно:

Определяем коэффициенты уравнения регрессии между нормированными переменными (2.13):

Соответственно выражению (2.22) записываем систему нормальных уравнений в виде:

                                 (3.3)

Решив систему (3.3), находим коэффициенты  и уравнение регрессии (2.13).

 

 

---

Дата добавления: 2018-04-05; просмотров: 226; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!