Предел и производная функции комплексного переменного
Производная функции комплексного переменного определяется, как и производная в действительной области:
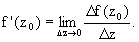
Здесь
z0, Dz _ комплексные и Df(z0) = f(z0+Dz) - f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих
1. Сумма и произведение дифференцируемых в точке функций, есть функция и справедливы равенства:
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :
3. Сложная функция f(j (z)) дифференцируема в точке z0, если в этой точке дифференцируема функцияj (z), а функция f(u) дифференцируема в точке u0,
где u0 = j (z0) и u = j (z). При этом в точке z0 имеет место формула:
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Например, рассмотрим функцию f(z) = z3.
По определению производной для любой точки z, принадлежащей комплексной области, записываем:
Предел существует для любой точки z, принадлежащей комплексной области и
(z3)' =3z2.
Аналогично можно получить:
(zn)' = nzn-1 (n - действительное число).
ПРИМЕР 1. Вычисление значения производной функции коплексного переменного в точке.
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),
то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей
|
|
|
u(x, y) = Re f(z), v(x, y) = Im f(z)
и выполняется условие Коши-Римана:
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
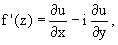
Элементарные свойства аналитической функции.
Арифметические свойства:
Если 
и 
аналитичны в области 
1. Функци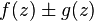и 
, 
и 
аналитичны в 
.
2. Если в области не обращается в ноль, то 
будет аналитична в
3. Если 
в области не обращается в ноль, то 
будет аналитична в .
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Обратное в общем случае неверно.
Некоторые свойства аналитических функций близки к свойствам многочленов, что, впрочем, и неудивительно — определение аналитичности в смысле Вейерштрасса свидетельствует о том, что аналитические функции — в некотором роде предельные варианты многочленов. Допустим, согласно основной теореме алгебры любой многочлен может иметь нулей числом не более его степени. Для аналитических функций справедливо аналогичное утверждение, вытекающее из теоремы единственности в альтернативной форме:
|
|
|
· Если множество нулей аналитической в односвязной области функции имеет в этой области предельную точку, то функция тождественно равна нулю.
· Для функции от нескольких действительных переменных аналитичности по каждой из переменных недостаточно для аналитичности функции. Для функции от нескольких комплексных переменных аналитичности по каждой из переменных достаточно для аналитичности функции (Теорема Хартогса).
Дата добавления: 2018-04-04; просмотров: 311; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!