Векторное поле. Векторные линии
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем.
Векторное поле на евклидовом пространстве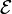 
определяется как вектор-функция точки пространства, отображающая это пространство в (на) себя:
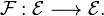
То есть, каждой точке пространства сопоставляется некоторый вектор (значение векторного поля в данной точке пространства). В общем случае этот вектор различается для разных точек пространства, то есть в общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространстве.
Интегральной кривой (также — векторной линией, для силовых полей — силовой линией, для поля скорости движения жидкости или газа — линией тока; первые термины являются общими, остальные — их синонимами в зависимости от контекста) для поля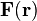 
называется кривая 
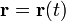, касательная к которой во всех точках кривой совпадает со значением поля: 
На картинке - силовые линии магнитного поля. ->
Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.
Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.
|
|
|
Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.
Линейный интеграл и циркуляция векторного поля.
Определение линейного интеграла. Пусть в пространственной области V определено непрерывное векторное поле(M), L - гладкая кривая, расположенная в V. Линейным интегралом поля вдоль линии L называется криволинейный интеграл по длине дуги от скалярного произведения (M) на единичный касательный вектор (M): .
Как и поток, этот интеграл может представляться различным образом. Так, если учесть, что произведение на даёт изменение радиуса-вектора точки М, т.е. ,то и . Следовательно, линейный интеграл может быть выражен и через линейный интеграл по координатам.
Основные свойства линейного интеграла.
1. Линейность.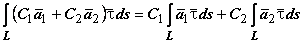 
;
2. Аддитивность.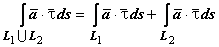 
. Направление на каждой из частей L1 и L2 должно быть таким же, как и на всей кривой 
;
|
|
|
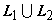3. При изменении направления вдоль L линейный интеграл меняет знак. Это следует из того, что вектор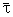 
(M) меняется на - 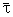(M).
4. Если L - векторная линия поля, и движение происходит в направлении поля, то W>0. В этом случае вектор 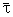(M) коллинеарен 
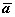(M), поэтому 
.
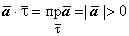Вычисление линейного интеграла. Как и любой криволинейный интеграл, линейный интеграл вычисляется сведением к определённому интегралу по параметру на кривой; обычно вычисляют криволинейный интеграл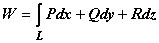 
. Если кривая при параметрическом задании имеет вид 
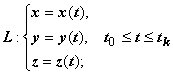, где 
- непрерывно дифференцируемые функции, то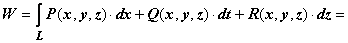 
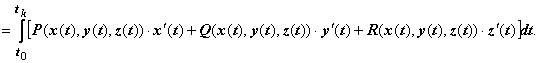Направление интегрирования определяется направлением движения по кривой.
Циркуляция векторного поля.
Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой С: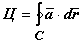 
.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны; вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше |Ц|, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.
|
|
|
Дата добавления: 2018-04-04; просмотров: 748; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!