Градиент. Связь между производной скалярного поля и градиентом
Скалярное поле. Производная по направлению.
Скалярное поле:
Если каждой точке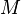 
заданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое (обычно — действительное) число 
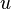, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая 
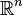в 
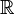(скалярная функция точки пространства).
Чаще других в приложениях встречаются:
Функция трёх переменных: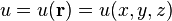 
(скалярное поле на (в) трёхмерном пространстве, называемое иногда пространственным полем).
Функция двух переменных: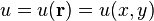 
(скалярное поле на (в) двумерном пространстве, называемое иногда плоским полем).
В физике и многих других приложениях поле, вообще говоря, зависит также от времени:
,
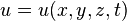при этом операции над полем (такие, как градиент) используются по-прежнему 3-мерные, то есть, несмотря на добавление еще одной независимой переменной, по существу при этом поле рассматривается как поле в пространстве размерности 3, а не 4. Те же соображения касаются случаев, когда поле зависит, кроме пространственных координат, ещё от каких-то других параметров: эти параметры могут быть явно указаны в функциональной зависимости, что, однако, не меняет размерности основного пространства, в котором рассматривается поле.
Примеры скалярных полей на трёхмерном пространстве:
-Температура (подразумевается, что она вообще говоря разная в разных точках пространства);
|
|
|
-Электростатический потенциал;
-Потенциал в ньютоновской теории тяготения;
-Поле давления в жидкой среде.
Примеры плоских (двумерных) скалярных полей:
-Глубина моря, отмеченная каким-либо образом на плоской карте;
-Плотность заряда на плоской поверхности проводника.
-Обычно под скалярным полем понимается поле, инвариантное при преобразованиях координат.
Производная по направлению:
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию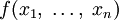 
от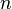 
аргументов в окрестности точки 
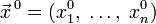. Для любого единичного вектора 
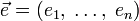определим производную функции 
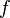в точке 
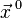по направлению 
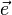следующим образом:
|
|
|
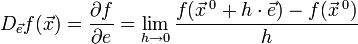
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .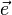
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
Связь с градиентом:
Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
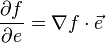
Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке
Градиент. Связь между производной скалярного поля и градиентом.
Градиент — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Для случая трёхмерного пространства, градиентом называется векторная функция с компонентами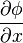 
, 
, 
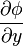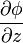где φ — некоторая скалярная функция координат x, y, z.
|
|
|
Градиент обозначается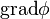 
или, с использованием оператора набла, 
.
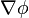Из определения градиента следует, что:
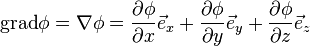
Свойства:
Для любого постоянного числа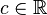 
и скалярных полей 
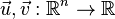справедливо следующее:
1) 
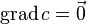
2)Линейность
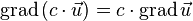
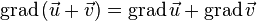
3)Правило Лейбница
, где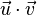 
— скалярное произведение векторов 
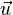и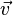 
Связь с производной по направлению:
Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции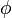 
по направлению 
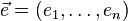равняется скалярному произведению градиента 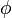наединичный вектор 
: 
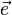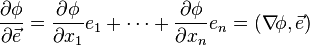
Дата добавления: 2018-04-04; просмотров: 948; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!