Действия над комплексными числами в алгебраической форме
Сравнение:
означает, что 
и 
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение:
Вычитание:
Умножение:
Деление:
В частности: 
Действия над комплексными числами в показательной форме. Формула Муавра.
Формула Муавра:
Эта формула помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
где 
— модуль, а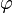 
— аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формула справедлива при любом целом n, не обязательно положительном.
Аналогичная формула применима также и при вычислении корней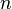 
-ой степени из ненулевого комплексного числа:
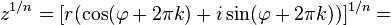
Отметим, что корни 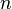-й степени из ненулевого комплексного числа всегда существуют, и их количество равно 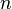. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного 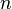-угольника, вписанного в окружность радиуса 
с центром в начале координат (см. рисунок).
Действия над комплексными числами в показательной форме:
Рассмотрим произвольное комплексное число, записанное в тригонометрической форме: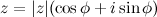 
. По формуле Эйлера
а тогда
Следовательно, любое комплексное число можно представить в так называемой показательной форме:
Такая форма представления позволяет дать наглядную интерпретацию операциям умножения комплексных чисел, их деления и возведения комплексного числа в степень. Например, умножение комплексного числа 
на комплексное число 
выглядит следующим образом:
|
|
|
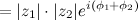
То есть, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично можно довольно легко найти частное от деления комплексного числа на комплексное число :
Отсюда получаем правило, что для того чтобы найти частное двух комплексных чисел, надо поделить их модули и отнять аргументы.
Для возведения комплексного числа 
в целую степень 
нужно представить это число в показательной форме 
, модуль возвести в степень, а аргумент увеличить в раз:
Задание. Записать комплексное число 
в показательной форме.
Решение. Найдем модуль и аргумент заданного комплексного числа:
Тогда
Ответ. 
Кривые на комплексной плоскости.
Области на комплексной плоскости.
Функция комплексного переменного. Однозначные и многозначные функции. Примеры.
ФКП:
Это понятие — обобщение предыдущего варианта:
.
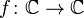Такими функциями занимается отдельная область математического анализа — теория функций комплексного переменного, или комплексный анализ.
|
|
|
Функция также может быть представлена в виде
,
однако имеется более глубокая связь между u и v. Например, для того, чтобы функция 
была дифференцируема, должны выполняться условия Коши — Римана:
;
.
Примерами аналитических функций комплексного переменного являются: степенная функция, экспонента, гамма-функция, дзета-функция Римана и многие другие, а также обратные им функции и любые их комбинации. Однако действительная часть комплексного числа 
, комплексная часть 
, компексное сопряжение 
, модуль 
и аргумент 
аналитическими функциями комплексного переменного не являются, так как не удовлетворяют условиям Коши — Римана.
Примеры:
Степенна́я фу́нкция — функция 
, где 
(показатель степени) — некоторое вещественное число. К степенным часто относят и функцию вида 
, где k — некоторый масштабный множитель. Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом.
Экспоне́нта — показательная функция 
, где e — Число Эйлера ( 
).
Примером многозначной функции может служить извлечение квадратного корня числа.
|
|
|
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
,
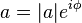то (см. Формула Муавра)
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом в итоге в ответе получаются два различных результата.
Дата добавления: 2018-04-04; просмотров: 816; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!