Проверить независимость двух характеристик по критерию Стьюдента

Построить линии регрессии.

Постановка задачи.

По выборке 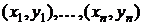из двумерного нормального распределения проверить гипотезу независимости компонентов наблюдаемого случайного вектора 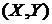. Построить линии регрессии одного из признаков по другому признаку. Найти наилучший прогноз признака 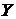при фиксированном значении признака .

Теоретические основы.

См. стр. 59-62 и стр. 65-67 пособия [4].

Вычисления.

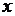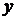Для вычисления выборочного коэффициента корреляции пакет Excel располагает встроенной функцией КОРРЕЛ(массив1; массив2), где массив1 и массив2 – ссылки на ячейки с наблюдениями над и . Количество 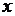-ов должно совпадать с количеством 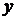-ов.

Пример.

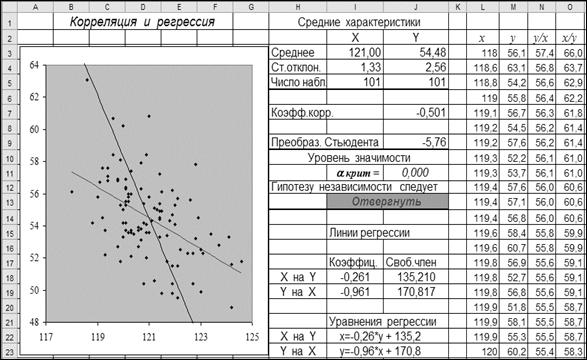
Ниже приведен образ листа Excel с необходимыми вычислениями. Данные по первому признаку те же, что использовались при первичной статистической обработке. Кроме того, здесь приведены результаты построения линий среднеквадратической регрессии. Гипотеза независимости проверяется при двухсторонней альтернативе.

При 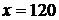наилучший прогноз второй характеристики .

a Порядок вычислений.

В целях удобства, лучше всего сначала скопировать данные на рабочий лист. Итак, пусть наши данные располагаются в ячейках L3:M103 (101 значение по каждому из признаков).

1) Подсчитать средние значения, стандартные отклонения и число наблюдений для обоих признаков (ячейки I3:J5);

2) вычислить коэффициент корреляции (ячейка J7)

Ø =КОРРЕЛ(L3:L103; M3:M103)

3) вычислить преобразование Стьюдента для r (ячейка J9)

Ø =КОРЕНЬ(I5-2)*J7/КОРЕНЬ(1-J7^2)

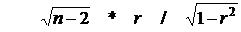{ – это просто пояснение };

4) вычислить критический уровень значимости для двухсторонней альтернативы (ячейка J11)

Ø =СТЬЮДРАСП(ABS(J9); I5-2 ;2)

последний аргумент – число хвостов – для двухсторонней альтернативы равен 2;

5) сделать вывод о значимости гипотезы независимости

– ячейки I13:J13.

Перейти к построению линий регрессии.

6) Вычислить коэффициенты регрессии X на Y

Ø =J7*I4/J4 – ячейка I18 – коэффициент регрессии;

=I3-I18*J3 – ячейка J18 – свободный член;

7) вычислить коэффициенты регрессии Y на X

Ø =J7*J4/I4 – ячейка I19 – коэффициент регрессии;

Ø =J3-I19*I3 – ячейка J19 – свободный член;

8) вычислить прогноз признака Y по значению признака X=120

Ø = 120*I19+J19 .

Построить графики линий регрессии.

9) упорядочить данные по признаку X

Ø выделить все ячейки данных (как x-ы, так и y-и), начиная со столбца L, и нажать кнопку меню Excel (если начать выделение со столбца M, то упорядочение произойдет по признаку Y);

10) в ячейках N3, O3 вычислить значения функций регрессии (значения переменной y по значению переменной x)

Ø =L3*$I$19+$J$19 – регрессия Y на X;

Ø =(L3-$J$18)/$I$18 – регрессия X на Y;

11) скопировать ячейки N3, O3 параллельно данным столбца L.

Теперь все готово для построения графиков линий регрессии.

12) Выделить данные в четырех столбцах L, M, N, O;

13) вызвать “Мастера построения диаграмм”;

14) выбрать “Точечную диаграмму со значениями, соединенными сглаживающими линиями”;

15) после двух нажатий кнопки выбрать закладку \\Легенда// и удалить легенду из графика, сняв галочку на переключателе “Добавить легенду”;

16) ;

17) привести вид полученного графика в соответствие с приведенным выше стандартом

Ø убрать маркеры с линий регрессии;

Ø убрать линию, соединяющую исходные данные;

Ø изменить границы шкал по оси OX и по оси OY

– общий принцип – щелкнуть правой кнопкой мыши в области изменяемого элемента и выбрать изменение «Формата».

Замечание 1. Отрицательное значение коэффициента корреляции говорит о том, что с ростом одного из признаков следует ожидать уменьшение другого признака – сравните с аналогичным выводом, сделанным при проверке независимости по критерию сопряженности хи-квадрат.

Замечание 2. Гипотеза независимости отвергается с очень высоким уровнем значимости (на листе приведено значение 0,000, означающее, что действительное значение меньше 0,001). Однако, величина коэффициента корреляции -0,501 имеет низкую практическую значимость – см. замечание 2 на стр. 66 пособия [4].

Контрольные вопросы.

1. Сформулируйте статистическую задачу.

2. Запишите формулу для выборочного коэффициента корреляции и найдите (вручную) его значение по следующим данным: (1;2), (2;5), (3;8).

Ответ: см. [4] стр. 61.

3. Не вычисляя, скажите, чему равен коэффициент корреляции для следующих данных: (1;2), (2;4), (3;6), (7;14)?

Ответ: см. [4] стр. 60.

4. Является ли выборочный коэффициент корреляции несмещенной (состоятельной) оценкой для истинного коэффициента корреляции?

Ответ: см. [4] стр. 61.

5. Какими свойствами обладает коэффициент корреляции?

Ответ: см. [4] стр. 60.

6. Как изменится значение коэффициента корреляции между ростом и весом человека, если значение веса измерять сначала в килограммах, а затем в граммах?

Ответ: см. [4] стр. 60.

7. Почему (и когда) гипотезу независимости можно проверять, основываясь на значениях выборочного коэффициента корреляции?

Ответ: см. [4] стр. 65.

8. Выпишите преобразование Стьюдента для выборочного коэффициента корреляции.

Ответ: см. [4] стр. 65.

9. Чему равен критический уровень значимости при односторонней альтернативе?

Ответ: см. [4] стр. 66.

10. В чем отличие статистической значимости от практической значимости?

Ответ: см. [4] стр. 66-67.

11. Что такое линейная регрессия?

Ответ: см. [4] стр. 59-60.

12. Выпишите уравнение линейной регрессии 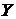на 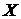. Можно ли по этому уравнению вычислить приближенное значение признака 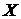, если задано значение признака ?

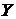Ответ: см. [4] стр. 60.

13. В целях упрощения вычислений очень часто значения одного (или обоих) признаков уменьшают на одну и ту же константу. Например, если все данные располагаются в пределах от 0 до 20, то, вычтя из всех данных число 10, мы сможем проводить вычисления даже без калькулятора. Как при этом изменяться коэффициенты линии регрессии?

Ответ: см. [4] стр. 60.

14. Исходя из персональных данных, найдите наилучший прогноз признака 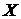, если значение признака .

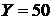15. Известно, что высота , с которой падает предмет, и время его падения удовлетворяют соотношению 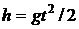, где 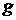– ускорение свободного падения. Как с помощью методов регрессионного анализа оценить величину 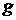по ряду связанных замеров и ?

16. В каком случае обе линии регрессии совпадут?

Ответ: см. [4] стр. 60.

17. Как будут располагаться линии регрессии, если коэффициент корреляции близок к 0?

Ответ: см. [4] стр. 60.

18. Как будут располагаться линии регрессии, если коэффициент корреляции близок к 1?

Ответ: см. [4] стр. 60.

Встроенные функции Excel.

Здесь мы опишем возможности Excel при вычислении статистических функций и дадим пояснения к способу их вызова.

¨ Нормальное распределение.

См. стр. 16-17 пособия [4].

Практически любой справочник по математической статистике содержит таблицы функции 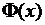и её квантилей. Так как стандартное нормальное распределение симметрично, то эти таблицы составляют для значени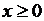й и . Приведем фрагмент таблицы из сборника [1].

Таблица 1.1. Функция нормального распределенияФ(x)

x	0	1	2	3	4	…	8	9
	…
2,05	0,97 9818	9867	9915	9964	0012	…	0205	0253
06	0,98 0301	0349	0396	0444	0491	…	0680	0727
07	0774	0821	0867	0914	0960	…	1145	1191
	…

Слева в таблице представлено входное значение 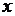с точностью до второго знака после запятой. Третий знак указан в самой верхней строке таблицы. С целью представления на одном листе по возможности большей информации, таблица разбита на блоки (выделенные чертой), в которых числа имеют несколько одинаковых первых цифр. Эти совпадающие части приведены только для одного значения (в столбце под верхней первой ячейкой с цифрой 0). Так, например,

Ф(2,052) = 0,97 9915, Ф(2,058) = 0,98 0205, Ф(2,074) = 0,98 0960.

Для нахождения квантилей можно использовать таблицу исходной функции распределения, отыскивая значение вероятности внутри таблицы и находя соответствующее входное значение. Например, при 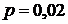верхняя p-квантиль (то есть решение уравнения 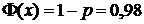) будет находиться где-то между 2,053 и 2,054, так как 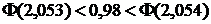. Простая линейная аппроксимация дает .

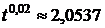В этом же сборнике [1] имеется таблица значений обратной функции нормального распределения, иными словами – таблица p-квантилей (не верхних).

Таблица 1.3. Функция, обратная функции нормального распределения

p	0	1	2	3	4	…	8	9
	…
977	1,9 9539	9723	9908	0093	0279	…	1030	1219
978	2,0 1409	1600	1792	1984	2177	…	2957	3154
979	3352	3551	3750	3950	4151	…	4964	5169
0,980	5375	5582	5790	6000	6208	…	7056	7270
	…

Таким образом, 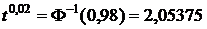, что весьма близко к полученному выше приближенному значению.

Пакет Excel располагает четырьмя функциями, связанными с нормальным распределением. Для вызова этих функций необходимо

1) вызвать «Мастера Функций»

Ø нажать кнопку панели инструментов или

перейти в подраздел “Функция” раздела “Вставка” главного меню Excel;

2) в категории “Статистические” найти соответствующую функцию;

3) заполнить таблицу аргументов функции.

Альтернативный способ вызова состоит в непосредственном обращении к соответствующей функции из ячейки листа Excel. Общий вид такого обращения можно представить следующим образом:

=ИМЯФУНКЦИИ(аргумент1;аргумент2; …)

Аргументами функции могут быть либо числа, либо ссылки на ячейки, их хранящие.

Рассмотрим каждую из этих функций по отдельности.

1. НОРМСТРАСП – функция стандартного нормального распределения 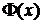. Аргумент – значение 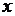(любое число).

2. НОРМСТОБР – обратная функция стандартного нормального распределения 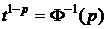. Аргумент – 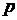(число от 0 до 1).

3. НОРМРАСП – функция распределения 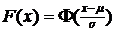или функция плотности 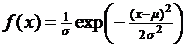нормального закона. Имеет 4 аргумента:


	x	не требует пояснений
	Среднее	среднее значение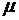
	Стандартное_откл	корень из дисперсии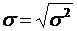
	Интегральная	0 (или FALSE) – вычисляется плотность, 1 (или TRUE) – функция распределения

4. НОРМОБР – функция, обратная функции нормального распределения 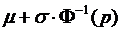. Имеет 3 аргумента, аналогичные первым трем аргументам предыдущей функции.

Приведем несколько примеров применения этих функций.

Функция Excel	Значение в ячейке	Характеристика распределения
=НОРМСТРАСП(2,058)	0,98020500	Ф(2,058) – функция распределения
=НОРМСТОБР(0,05)	-1,64485348	t^0,⁹⁵ – 5%-квантиль
=НОРМРАСП(-1; 0; 1; 1)	0,15865526	Ф((2,058-0)/1) – функция распределения
=НОРМРАСП(-1; 0; 1; 0)	0,24197073	φ((2,058-0)/1) – функция плотности
=НОРМОБР(0,95; 0; 1)	1,64485348	0+1* t^0,⁰⁵ – верхняя 5%-квантиль

Задание. Объясните совпадение значений (с точностью до знака) во второй и пятой строках этой таблицы.

¨ Хи-квадрат распределение.

См. стр. 18-19 пособия [4].

Сборник таблиц [1] содержит значения так называемого интеграла вероятностей хи-квадрат – в нашей терминологии это просто функция надежности . Таблица имеет два входа – по числу степеней свободы (верхняя строка) и по аргументу функции (левый столбец).

Таблица 2.1а. Интеграл вероятностей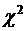

x	m=16		…	m=20
x	P	-Δ	…	P	-Δ
…	…			…
15,0	0,52464	3627	…	0,77641	2929
5	48837	3541	…	74712	3050
…	…			…

Здесь, кроме значения функции распределения (столбец P), приведены также первые разности этой функции (столбец -Δ), точнее, только 5 значащих цифр после запятой без первых нулей. Таким образом, 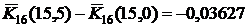(после запятой поставлен один ноль, чтобы получилось пять цифр). Есл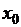и и 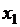– два рядом стоящие значения аргумента, то для нахождения значения функции в промежуточной точке 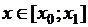можно применить аппроксимацию . В приведенном нами фрагменте 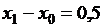. Поэтому .

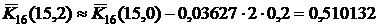Значения верхних p-квантилей 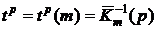распределения хи-квадрат содержатся в следующей таблице на стр.166 сборника [1].

Таблица 2.2а. Процентные точки распределения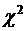

Q m	…	97,5%	95%	…	5%	2,5%	…
…	…
19	…	8,907	10,117	…	30,144	32,852	…
20	…	9,591	10,851	…	31,410	34,170	…
…	…

Вход в таблицу осуществляется по числу степеней свободы (m в левом столбце) и по вероятности, выраженной в процентах (Q в верхней строке). Таким образом, .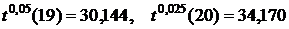

Пакет Excel предоставляет возможность вычисления как значений функции надежности 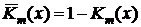, так и значений p-квантилей хи-квадрат распределения. Эти функции называются ХИ2РАСП и ХИ2ОБР. Рассмотрим несколько примеров применения этих функций.

Функция Excel	Значение в ячейке	Характеристика распределения
=ХИ2РАСП(15,2; 16)	0,510041	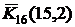– функция надежности
=ХИ2РАСП(15; 20)	0,776408	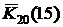– функция надежности
=ХИ2ОБР(0,05; 19)	30,14351	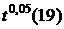– верхняя 5%-квантиль
=ХИ2ОБР(0,025; 20)	34,16958	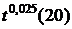– верхняя 2,5%-квантиль

¨ Распределение Стьюдента.

См. стр. 19-20 пособия [4].

Таблицы распределения Стьюдента также имеются в любом справочнике по математической статистике. Приведем здесь фрагмент соответствующей таблицы из сборника [1].

Таблица 3.1а. Функция распределения Стьюдента

k t	11	12	…	19	20
…	…
2,0	0,9646	0,9657	…	0,9700	0,9704
1	9702	9712	…	9753	9757
…	…

Эта таблица имеет два входа – число степеней свободы 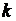(верхняя строка) и аргумент функции 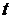(левый столбец). Из этой таблицы находим, что . При степенях свободы больше 20 можно воспользоваться нормальным приближением: .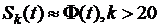

Следующая таблица указанного сборника [1] содержит значения верхних 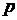-квантилей 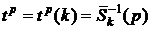. Эта таблица также имеет два входа – число степеней свободы (левый столбец) и вероятность в процентах 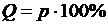(верхняя строка). Для наглядности целые части вместе с запятой приведены только для верхних чисел в блоке из пяти чисел.

Таблица 3.2. Процентные точки распределения Стьюдента

Q k	…	10%	5%	2,5%	…	0,05%
…	…
19	…	1,3277	1,7291	2,0930	…	3,8834
20	…	3253	7247	0860	…	8495
…	…

Таким образом, .

В пакете Excel имеются встроенные функции

СТЬЮДРАСП, вычисляющая функцию надежности, и

СТЬЮДРАСПОБР, вычисляющая верхние квантили.

Функция СТЬЮДРАСП имеет три аргумента. Кроме двух естественных (аргумента 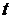и числа степеней свободы 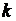), при обращении к этой функции требуется указать количество хвостов распределения, которые нужно учитывать (1 или 2). Под “хвостом” распределения понимается любой интервал с одним конечным и одним бесконечным концом. Например, при вычислении функции надежности ищется вероятность попадания в область 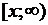. Поэтому - это функция СТЬЮДРАСП с одним “хвостом”. Очень часто в статистической практике требуется найти вероятность попадания в область 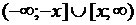при 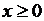, то есть в область с двумя “хвостами”. Легко видеть, что функция, вычисляющая вероятности таких симметричных интервалов, представляет собой не что иное, как функцию надежности распределения модуля .

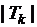Обращение к функции СТЬЮДРАСПОБР вполне тривиально и полностью аналогично обращению к функции ХИ2ОБР (см. выше).

¨ Показательное (экспоненциальное) распределение.

См. стр. 21 пособия [4].

Как функция плотности, так и функция распределения показательного закона могут быть вычислены посредством калькулятора. В Excel обе эти функции можно вычислить, воспользовавшись функцией EXP(…).

¨ Биномиальное распределение.

См. стр. 22 пособия [4].

В пакете Excel имеется возможность вычисления функции

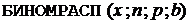которая при 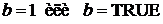есть не что иное, как функция распределения 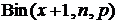(обратите внимание на различие в первом аргументе этих функций). Четвертый параметр функции БИНОМРАСП, если он не равен нулю, указывает на необходимость вычисления именно функции распределения, то есть суммы всех биномиальных вероятностей до включительно (в отличие от функции 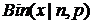, которая вычисляет вероятности до 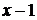). При функция БИНОМРАСП вычисляет индивидуальную вероятность 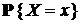. Приведем несколько примеров.

Функция Excel	n	p	Вероятность	Результат
БИНОМРАСП(3;10;0,5;1)	10	0,5		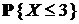0,171865
БИНОМРАСП(3;10;0,5;0)	10	0,5		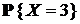0,117188
1-БИНОМРАСП(29;100;0,5;1)	100	0,5		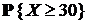0,999984
1-БИНОМРАСП(30;100;0,5;0)	100	0,5		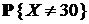0,999977

Дата добавления: 2018-04-05; просмотров: 679; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 7 89

Мы поможем в написании ваших работ!