Двухвыборочный критерий Стьюдента

 

Постановка задачи.

 

Имеются две выборки , относящиеся к двум независимым группам наблюдений одной и той же характеристики, подчиняющейся нормальному закону с одинаковыми для обеих выборок дисперсиями. Требуется проверить гипотезу однородности выборок, то есть гипотезу совпадения средних значений.

 

Теоретические основы.

См. стр. 42-43 пособия [4].

 

Вычисления.

При построении этого критерия применяются те же вспомогательные функции Excel, что для одновыборочного критерия Стьюдента (задание 5).

 

Пример.

В качестве иллюстрации рассмотрим пример изучения верхнего артериального давления у пациентов, прошедших два различных курса лечения. В первую группу мы отнесли данные о пациентах, лечившихся по новой методике, во вторую – по стандартной методике. Естественные ожидания авторов новой методики состоят в том, что среднее первой выборки будет меньше среднего второй выборки. 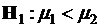Таким образом, необходимо проверить гипотезу  при альтернативе  (напомним: альтернатива суть ожидания исследователя). Критерий Стьюдента для такой гипотезы полностью совпадает с критерием Стьюдента для простой гипотезы  при той же альтернативе.

 

 

	A	B	C	D	E	F	G	H
1	1-я выборка	2-я выборка
2	139	119				Выборочные характеристики
3	136	143
4	126	139				1-я выборка	2-я выборка
5	143	130			Среднее	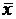144,6	131,375
6	154	144			Ст.Отклон.	10,03	10,26
7	156	114			Ош.средн. (+-)	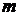2,49	6,46
8	155	135			Объем выборки	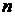10	8
9	143	127				Уровень значимости		0,05
10	157					Статистика Стьюдента
11	139						2,59
12
13					Гипотеза	Альтернатива		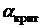Принимается
14					Равны	1-я меньше	0,99	Гипотеза
					Вывод: выборочные данные не свидетельствуют в пользу новой методики.

 

a  Порядок вычислений  здесь вполне идентичен вычислениям, проводимым при реализации одновыборочного критерия Стьюдента. Отличия заключаются только в том, что не надо вычислять разности, а статистика Стьюдента (ячейка G11) вычисляется как

Ø =(F5-G5)*КОРЕНЬ(F8*G8*(F8+G8-2)/((F8+G8)*(F8*F6+G8*G6))

{ }.

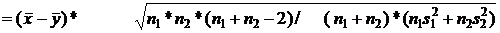Контрольные вопросы.

1. Сформулируйте статистическую задачу.

2. Как вычисляется статистика двухвыборочного критерия Стьюдента?

Ответ: см. [4] стр. 43

3. Почему к рассматриваемым данным нельзя применить одновыборочный критерий Стьюдента?

Ответ: см. [4] стр. 37-38, 42.

4. Когда следует применять критерий Стьюдента, а когда критерий Вилкоксона?

Ответ: см. [4] стр. 42-43.

5. Чему равен критический уровень значимости для критерия Стьюдента при двухсторонней альтернативе; при односторонней альтернативе типа – «в первой группе больше»?

Ответ: см. [4] стр. 43.

6. Можно ли к рассматриваемым данным применить критерий однородности хи-квадрат?

Ответ: см. [4] стр. 48.

7. Что такое ошибка среднего? Какую смысловую нагрузку она несет применительно к рассматриваемому критерию?

Ответ: см. [4] стр. 55.

8. Какой критерий следует применять для проверки гипотезы равенства средних значений, если известно, что обе выборки получены из экспоненциального распределения?

Ответ: см. [4] стр. 43, 48.

Задание 8.

Критерий Вилкоксона.

 

Постановка задачи.

 

Имеются две выборки , относящиеся к двум независимым группам наблюдений одной и той же характеристики. Требуется проверить гипотезу однородности выборок в ситуации, когда ожидается, что значения в 1-й выборке будут меньше значений во второй выборке.

 

Теоретические основы.

См. стр. 43-46 пособия [4].

 

Вычисления.

Для нахождения ранга значения x в ряду данных Q в среде Excel можно использовать функцию РАНГ(x; Q; 1) (третий аргумент функции, равный 1, указывает на порядок расположения по возрастанию). Всем совпадающим значениям в ряду Q  функция РАНГ присваивает одинаковое значение, равное меньшему рангу. Чтобы исправить её в соответствии с вышеописанной схемой, можно поступить следующим образом.

1. Для каждого значения  1-й выборки подсчитать количество данных (в обеих выборках), совпадающих с , воспользовавшись функцией                                                                                   СЧЁТЕСЛИ(Q; x).

2. Если таких значений наберется K  штук, то их средний ранг будет равен R+(K-1)/2, где R – результат применения функции РАНГ к значению .

 

Для вычисления приближенного значения уровня значимости с помощью нормальной аппроксимации можно воспользоваться функцией НОРМРАСП.

Пример.

Обратимся снова к данным, иллюстрировавшим применение двухвыборочного критерия Стьюдента. Для этих данных как раз ожидаемо, что первая выборка (результат лечения новым препаратом) будет “левее” второй выборки. Поэтому при отсутствии информации о нормальности распределения выборок вполне уместно будет применить критерий Вилкоксона.

	A		B	C	D	E	F	G
1	1-я выборка		2-я выборка	Число равных	Ранги 1-й выборки
2	139		119	3	9		Среднее статистики Вилкоксона
3	134		143	1	6			95,5
4	126		139	1	3		Дисперсия статистики Вилкоксона
5	143		130	3	12			126,67
6	154		144	1	15
7	156		114	1	17		Приближенное значение
8	155		135	1	16		уровня значимости
9	143		127	3	12		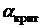=	0,972
10	157			1	18
11	139			3	9
12				Скрит =75
13	Количество			Статистика Вилкоксона			Гипотезу однородности следует
14	10	8		117			принять	на уровне > 95%
15				Вывод: выборочные данные не свидетельствуют в пользу новой методики.
16

 

a  Порядок вычислений.

1) В ячейке C2 вычислить количество совпадений с 1-ым элементом 1-ой выборки

Ø =СЧЕТЕСЛИ($A$2:$B$11; A2)

2) в ячейку D2 ввести функцию вычисления ранга 1-ого элемента 1-ой выборки

Ø =РАНГ(A2; $A$2:$B$11; 1)+(C2-1)/2

(не забудьте про знаки $);

3) скопировать ячейки C2 и D2 параллельно данным столбца A;

4) в ячейках A14 и B14 подсчитать количество данных 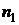  и 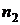  в каждой выборке;

5) найти в сборнике таблиц [1] значение критической константы  для полученных значени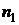й   и 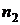 (ячейка D12);

6) в ячейке B14 вычислить сумму рангов столбца D (статистику Вилкоксона)

Ø =СУММ(D2:D11)

7) сравнив полученное значение с , сделать вывод об однородности или неоднородности выборок

Ø в нашем случае нет оснований утверждать, что в первой выборке значения меньше, чем во второй: .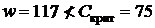

 

С целью подтверждения вывода вычислить приближенное значение критического уровня значимости:

 

8) в ячейке G3 вычислить среднее значение статистики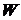

Ø =A14*(A14+B14+1)/2+0,5

9) в ячейке G5 вычислить дисперсию статистики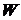

Ø =A14*B14*(A14+B14+1)/12

10) в ячейке G9 вычислить критический уровень значимости

Ø =НОРМРАСП(C14; G3; КОРЕНЬ(G5); 1)

11) сделать вывод об однородности выборок (ячейка G14).

 

Замечание.         Если бы мы в качестве альтернативы рассмотрели гипотезу 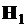: «2-ая выборка сдвинута влево», то нам пришлось бы отвергнуть гипотезу однородности в пользу альтернативы – . Однако, как говорится, “после выборки критическим значением не размахивают”. Как гипотеза, так и альтернатива должны выбираться до получения выборки. На худой конец, можно было бы выдвинуть двухстороннюю альтернативу – 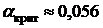 и, в случае её принятия, скажем, на 10%-ом уровне, выбрать направленность соотношения между выборками визуально.

 

Контрольные вопросы.

1. Сформулируйте статистическую задачу.

2. Как вычисляется статистика критерия Вилкоксона?

Ответ: см. [4] стр. 44.

3. При каких альтернативах следует прибегать к критерию Вилкоксона?

Ответ: см. [4] стр. 43.

4. Как присваивать ранги совпадающим значениям?

Ответ: см. [4] стр. 45.

5. Чему равен критический уровень значимости критерия Вилкоксона?

Ответ: см. [4] стр. 45.

6. Найдите по таблице критическое значение для объемов выборок 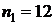 и .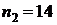

7. Какой критерий следует применять, если в качестве альтернативы к гипотезе однородности выдвинуто утверждение о том, что первая выборка получена из нормального распределения, а вторая из экспоненциального?

Ответ: см. [4] стр. 48.

 

Задание 9.

---

Дата добавления: 2018-04-05; просмотров: 956; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая123456789Следующая ⇒

---

Мы поможем в написании ваших работ!