Что называют задачами оптимизации? Приведите примеры задач оптимизации. Что такое экстремальный эксперимент?
Определения.
Под оптимизациейпонимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т. п.
В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. При решении инженерных задач их принято называтьпроектными параметрами, а в экономических задачах их обычно называют параметрами плана. В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т. п. Число п проектных параметров x1,x2,…,xп характеризует размерность (и степень сложности) задачи оптимизации.
Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией(или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция — это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные или экономические задачи.
Целевую функцию можно записать в виде
|
|
|

Примерами целевой функции, встречающимися в инженерных и экономических расчетах, являются прочность или масса конструкции, мощность установки, объем выпуска продукции, стоимость перевозок грузов, прибыль и т. п.
В случае одного проектного параметра (n = 1) целевая функция (6.1) является функцией одной переменной, и ее график — некоторая кривая на плоскости. При n = 2 целевая функция является функцией двух переменных, и ее график — поверхность в трехмерном пространстве.
Следует отметить, что целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать только некоторые дискретные значения, задаваться в виде таблицы и т. п. Во всех случаях она должна быть однозначной функцией проектных параметров.
Целевых функций может быть несколько. Например, при проектировании изделий машиностроения одновременно требуется обеспечить максимальную надежность, минимальную материалоемкость, максимальный полезный объем (или грузоподъемность). Некоторые целевые функции могут оказаться несовместимыми. В таких случаях необходимо вводить приоритет той или иной целевой функции.
Задачи оптимизации.
Можно выделить два типа задач оптимизации — безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (6.1) от действительных переменных и определении соответствующих значений аргументов на некотором множестве а n-мерного пространства.
|
|
|
Условные задачи оптимизации, или задачи с ограничениями, — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве а. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения равенствавыражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов, финансовые требования и т. п.
В результате ограничений область проектирования а, определяемая всеми п проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число М ограничений-равенств может быть произвольным. Их можно записать в виде

В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие. Это позволяет исключить некоторые параметры из процесса оптимизации, что приводит к уменьшению размерности задачи и облегчает ее решение. Аналогично могут вводиться также ограничения-неравенства, имеющие вид
|
|
|

Следует отметить особенность в отыскании решения при наличии ограничений. Оптимальное решение здесь может соответствовать либо локальному экстремуму (максимуму или минимуму) внутри области проектирования, либо значению целевой функции на границе области. Если же ограничения отсутствуют, то ищется оптимальное решение на всей области проектирования, т. е. глобальный экстремум.
Пример постановки задачи.
Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объемом V = 1 м3, причем желательно израсходовать на его изготовление как можно меньше материала.
При постоянной толщине стенок последнее условие означает, что площадь полной поверхности контейнера должна быть минимальной. Если обозначить через x1, х2, х3 длины ребер контейнера, то задача сведется к минимизации функции

Эта функция в данном случае является целевой, а условие (V — 1) — ограничением равенством, которое позволяет исключить один параметр:

Задача свелась к минимизации функции двух переменных. В результате решения задачи будут найдены значения проектных параметров х1, x2, а затем и х3.
|
|
|
Задачи на экстремум.
Одномерная задача оптимизациив общем случае формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функции у = f(x), заданной на множестве cr, и определить значение проектного параметра х е а, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из следующей теоремы.
Теорема Вейерштрасса. Всякая функция f(x), непрерывная на отрезке [а, b], принимает на этом отрезке наименьшее и наибольшее значения, т. е. на отрезке [а, b] существуют такие точки х1 и x2, что для любого х £ [а,b] имеют  место неравенства
место неравенства
Пример. Найти наименьшее и наибольшее значения функции f ’ (x) = x3/3 - х2 на отрезке [1,3].
Решение. Вычислим производную этой функции:

Приравнивая ее нулю, найдем критические точки:

Точка х = 0 лежит вне рассматриваемого отрезка, поэтому для анализа оставляем три точки: а = 1, x-i — 2, b = 3. Вычисляем значения функции в этих точках:

Сравнивая полученные величины, находим, что наименьшего значения функция f(x) достигает в точке х = 2, наибольшего — в точке х = 3, т. е.

Вопрос номер 2
Свойства:
· Симметричность относительно центра - алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю

где j-номер фактора, i- номер опыта, N- число опытов
· Условие нормировки - сумма квадратов элементов каждого столбца равна числу опытов

· Ортогональность матрицы - сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю

Геометрической интерпретацией полного факторного эксперимента 23 служит куб, координаты вершин которого задают условия опытов. Если поместить центр куба в точку основного уровня факторов, а масштабы по осям выбрать так, чтобы интервал варьирования равнялся единице, то получится куб, изображенный на рис. Куб задает область эксперимента, а центр куба является ее центром.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №23
1.Математическое планирование эксперимента с применением квадратической параболической однофакторной регрессионной модели. Проверка гипотезы об однородности дисперсий. Определение коэффициентов регрессионной модели.
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы
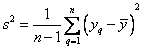 ,
,
а затем из всех дисперсий находится наибольшая  которая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
которая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
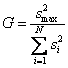 .
.
Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии и пользоваться формулой
 .
.
Если возникает предположение о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой формуле подсчитывается дисперсия воспроизводимости
 .
.
Далее находится величина
 ,
,
где
 .
.
Здесь число степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании эксперимента типа 2k это число равно числу опытов в матрице.
Бартлет показал, что величина  приближенно подчиняется
приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.
– распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.
Критерий Бартлета базируется на нормальном распределении. Если имеются отклонения от нормального распределения, то проверка неоднородности дисперсий может привести к ошибочным результатам.
Можно предложить использование F-критерия даже в тех случаях, когда число дисперсий больше двух. Делается это следующим образом. Из всех дисперсий выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет надобности применять критерий Бартлета.
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы
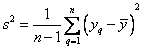 ,
,
а затем из всех дисперсий находится наибольшая  которая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
которая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
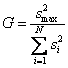 .
.
Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии и пользоваться формулой
 .
.
Если возникает предположение о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой формуле подсчитывается дисперсия воспроизводимости
 .
.
Далее находится величина
 ,
,
где
 .
.
Здесь число степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании эксперимента типа 2k это число равно числу опытов в матрице.
Бартлет показал, что величина  приближенно подчиняется
приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.
– распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.
Критерий Бартлета базируется на нормальном распределении. Если имеются отклонения от нормального распределения, то проверка неоднородности дисперсий может привести к ошибочным результатам.
Можно предложить использование F-критерия даже в тех случаях, когда число дисперсий больше двух. Делается это следующим образом. Из всех дисперсий выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет надобности применять критерий Бартлета.
- Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.
С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.
- Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения.
- Формула коэффициента регрессии. Rу/х = rху x (σу / σx)
где Rу/х — коэффициент регрессии;
rху — коэффициент корреляции между признаками х и у;
(σу и σx) — среднеквадратические отклонения признаков x и у.
В нашем примере [rху = - 0,96 коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)];
σх = 4,6 (среднеквадратическое отклонение температуры воздуха в осенне-зимний период;
σу = 8,65 (среднеквадратическое отклонение числа инфекционно-простудных заболеваний).
Таким образом, Rу/х — коэффициент регрессии.
Rу/х = -0,96 х (4,6 / 8,65) = 1,8, т.е. при снижении среднемесячной температуры воздуха (x) на 1 градус среднее число инфекционно-простудных заболеваний (у) в осенне-зимний период будет изменяться на 1,8 случаев.
- Уравнение регрессии. у = Му + Ry/x (х - Мx)
где у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х);
х — известная средняя величина другого признака;
Ry/x — коэффициент регрессии;
Мх, Му — известные средние величины признаков x и у.
Например, среднее число инфекционно-простудных заболеваний (у) можно определить без специальных измерений при любом среднем значении среднемесячной температуры воздуха (х). Так, если х = - 9°, Rу/х = 1,8 заболеваний, Мх = -7°, Му = 20 заболеваний, то у = 20 + 1,8 х (9-7) = 20 + 3,6 = 23,6 заболеваний.
Данное уравнение применяется в случае прямолинейной связи между двумя признаками (х и у).
- Назначение уравнения регрессии. Уравнение регрессии используется для построения линии регрессии. Последняя позволяет без специальных измерений определить любую среднюю величину (у) одного признака, если меняется величина (х) другого признака. По этим данным строится график — линия регрессии, по которой можно определить среднее число простудных заболеваний при любом значении среднемесячной температуры в пределах между расчетными значениями числа простудных заболеваний.
2. Ошибка опыта. Классификация ошибок опыта. Оценка ошибки опыта. Исключение грубых ошибок. Критерий Смирнова-Грабса
Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментального материала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку нужно оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов. Среднее арифметическое  равно сумме всех п отдельных результатов, деленной на количество параллельных опытов п
равно сумме всех п отдельных результатов, деленной на количество параллельных опытов п
 .
.
Ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.
Все ошибки делятся на три класса: промахи (грубые ошибки), систематические и случайные ошибки.
ПРОМАХ вызван резким нарушением условий измерения при отдельных наблюдениях. Это ошибка, связанная с толчком или поломкой прибора, грубым просчетом экспериментатора, непредвиденным вмешательством и т.д. грубая ошибка появляется обычно не более чем в одном–двух измерениях и резко отличается по величине от прочих ошибок. Наличие промаха может сильно исказить результат, содержащий промах.
СИСТЕМАТИЧЕСКОЙ ОШИБКОЙ называют составляющую погрешности измерений, остающуюся постоянной и закономерно изменяющуюся при повторных измерениях одной и той же величины.
Систематическая ошибка вызывается определенными причинами, величина ее остается постоянной (смещение нуля шкалы прибора, неравноплечность весов), либо изменяется по определенному (иногда довольно сложному) закону (неравномерность шкалы, неравномерность сечения капилляра термометра и т.д.).
Можно сказать, что систематическая ошибка – это смягченное выражение, заменяющее слова «ошибка экспериментатора».
Такие ошибки возникают из-за того, что:
- неточны измерительные приборы;
- реальная установка в чем-то отличается от идеальной;
- не совсем верна теория явления, т.е. не учтены какие-то эффекты.

Эта операция выполняется с помощью расчетного значения критерия Смирнова-Грабса по формулам:
при подозрении резко выделяющегося максимального значения Yimax:
 (6.2)
(6.2)
при подозрении резко выделяющегося минимального значения Yimin:
 (6.3)
(6.3)
где y - среднее значение входного параметра;
S{y} – среднее квадратическое отклонение выходного параметра.
Для первой строки опытов таблицы 6.1 в соответствия с формулами (6.2) и (6.3) имеем:


Табличное значение критерия Смирнова-Грабса Vт [P0= 0,95; m = 6] = 1,996 (Приложение 2 ). Так как VRmax<Vт и VRmin<Vт , то значения Yuυmax= 5,35 и Yuυmin= 4,00 не являются резко выделяющимися и остаются для дальнейшей статистической обработки.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №24
Функция отклика. Поверхность отклика.
Под моделью мы понимаем функцию отклика

Выбрать модель – значит выбрать вид этой функции, записать ее уравнение. Тогда останется спланировать и провести эксперимент для оценки численных значений констант (коэффициентов) этого уравнения.
Построим геометрический аналог функции отклика – поверхность отклика. Будем для наглядности рассматривать случай с двумя факторами.
Заметим, что в случае многих факторов геометрическая наглядность теряется. Мы попадаем в абстрактное многомерное пространство, где у нас нет навыка ориентирования. Приходится переходить на язык алгебры.
Мы хотим изобразить геометрически возможные состояния «черного ящика» с двумя входами. Для этого достаточно располагать плоскостью с обычной Декартовой системой координат. По одной оси координат будем откладывать в некотором масштабе значения (уровни) одного фактора, а по другой оси – второго. Тогда каждому состоянию «ящика» будет соответствовать точка на плоскости.

Для факторов существуют области определения. Это значит, что у каждого фактора есть минимальное и максимальное возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно. Если факторы совместимы, то границы образуют на плоскости некоторый прямоугольник, внутри которого лежат точки, соответствующие состояниям «черного ящика». Пунктирными линиями на рисунке обозначены границы областей определения каждою из факторов, а сплошными – границы их совместной области определения.
Метод наименьших квадратов.
Полиномиальная регрессионная модельи условия для ее определения
Регрессионная математическая модель, получаемая по данным активного эксперимента с традиционным методом планирования, имеет следующий полиномиальный вид:

В этом полиноме отсутствуют члены аijXiXi, характеризующие взаимодействие факторов. Метод определения коэффициентов регрессии а0, аi, аii, т.е. оценки истинных значений коэффициентов регрессии α0, αi, αii, на основе минимизации суммы квадратов отклонений экспериментальных значений Y от соответствующих значений YR, называется методом наименьших квадратов, или регрессионным анализом.
Применение метода наименьших квадратов правомерно при выполнении следующих условий:
1. Значения выходного параметра Yи в каждом и-м опыте матрицы планирования эксперимента представляют собой независимые, нормально распределенные случайные величины.
2. Дисперсии выходного параметра в различных опытах матрицы (в различных точках факторного пространства) однородны или пропорциональны некоторой функции от Xu.
3. Значения уровней факторов не являются линейной комбинацией от уровней остальных факторов.
4. Точность определения значений выходного параметра значительно ниже точности определения величины уровня фактора.
При выполнении этих условий оценки коэффициентов регрессии будут состоятельными, несмещенными, эффективными и достаточными.
Метод наименьших квадратов
Начнем с простого случая: один фактор, линейная модель. Интересующая нас функция отклика (которую мы будем также называть уравнением регрессии) имеет вид

Это хорошо известное уравнение прямой линии. Наша цель – вычисление неизвестных коэффициентов b0 и b1. Мы провели эксперимент, чтобы использовать при вычислениях его результаты. Как это сделать наилучшим образом?
Если бы все экспериментальные точки лежали строго на прямой линии, то для каждой из них было бы справедливо равенство
 ,
,
где i = 1, 2, ..., N – номер опыта. Тогда не было бы никакой проблемы. На практике это равенство нарушается и вместо него приходится писать
 ,
,
где 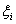 – разность между экспериментальным и вычисленным по уравнению регрессии значениями y в i-й экспериментальной точке. Эту величину иногда невязкой.
– разность между экспериментальным и вычисленным по уравнению регрессии значениями y в i-й экспериментальной точке. Эту величину иногда невязкой.
Мы хотим найти такие коэффициенты регрессии, при которых невязки будут минимальны. Это требование можно записать по-разному. В зависимости от этого мы будем получать разные оценки коэффициентов. Вот одна из возможных записей
 ,
,
которая приводит к методу наименьших квадратов.
Когда мы ставим эксперимент, то обычно стремимся провести больше (во всяком случае не меньше) опытов, чем число неизвестных коэффициентов. Поэтому система линейных уравнений
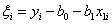
оказывается переопределенной и часто противоречивой (т. е. она может иметь бесконечно много решений или может не иметь решений). Переопределенность возникает, когда число уравнений больше числа неизвестных; противоречивость – когда некоторые из уравнений несовместимы друг с другом.
Только если все экспериментальные точки лежат па прямой, то система становится определенной и имеет единственное решение.
МНК обладает тем замечательным свойством, что он делает определенной любую, произвольную систему уравнений. Он делает число уравнений равным числу неизвестных коэффициентов.
Для определения двух неизвестных коэффициентов требуется два уравнения. Давайте попробуем их получить.

Минимум некоторой функции, если он существует, достигается при одновременном равенстве нулю частных производных по всей неизвестным, т. е.
 .
.
В явном виде это запишется как
 ,
,
 .
.
Окончательные формулы для вычисления коэффициентов регрессии, которые удобно находить с помощью определителей, имеют вид
 ,
,
 .
.
Величина  называется остаточной суммой квадратов (
называется остаточной суммой квадратов (  – значение параметра оптимизации, вычисленное из уравнения регрессии). МНК гарантирует, что эта величина минимально возможная.
– значение параметра оптимизации, вычисленное из уравнения регрессии). МНК гарантирует, что эта величина минимально возможная.
Обобщение на многофакторный случай не связано с какими-либо принципиальными трудностями.
Воспользуемся тем, что матрицы планирования ортогональны и нормированы, т.е.
 и
и 
Для любого числа факторов коэффициенты будут вычисляться по формуле

В этой формуле j = 0, 1, 2 ..., k – номер фактора. Ноль записан для вычисления b0.
Так как каждый фактор (кроме x0) варьируется на двух уровнях +1 и –1, то вычисления сводятся к приписыванию столбцу y знаков соответствующего фактору столбца и алгебраическому сложению полученных значений. Деление результата на число опытов в матрице планирования дает искомый коэффициент
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №25
1. Математическая модель. Выбор модели. Полиномиальные модели.
Математическое моделирование — процесс построения и изучения математических моделей реальных процессов и явлений. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и вопросы о применимости полученных таким образом результатов являются весьма содержательными.
Выбор модели
Под моделью мы понимаем функцию отклика

Выбрать модель – значит выбрать вид этой функции, записать ее уравнение. Тогда останется спланировать и провести эксперимент для оценки численных значений констант (коэффициентов) этого уравнения.
Построим геометрический аналог функции отклика – поверхность отклика. Будем для наглядности рассматривать случай с двумя факторами.
Заметим, что в случае многих факторов геометрическая наглядность теряется. Мы попадаем в абстрактное многомерное пространство, где у нас нет навыка ориентирования. Приходится переходить на язык алгебры.
Мы хотим изобразить геометрически возможные состояния «черного ящика» с двумя входами. Для этого достаточно располагать плоскостью с обычной Декартовой системой координат. По одной оси координат будем откладывать в некотором масштабе значения (уровни) одного фактора, а по другой оси – второго. Тогда каждому состоянию «ящика» будет соответствовать точка на плоскости.

Для факторов существуют области определения. Это значит, что у каждого фактора есть минимальное и максимальное возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно. Если факторы совместимы, то границы образуют на плоскости некоторый прямоугольник, внутри которого лежат точки, соответствующие состояниям «черного ящика». Пунктирными линиями на рисунке обозначены границы областей определения каждою из факторов, а сплошными – границы их совместной области определения.

Чтобы указать значение параметра оптимизации, требуется еще одна ось координат. Пространство, в котором строится поверхность отклика, мы будем называть факторным пространством. Оно задается координатными осями, по которым откладываются значения факторов и параметра оптимизации. Размерность факторного пространства зависит от числа факторов. При многих факторах поверхность отклика уже нельзя изобразить наглядно и приходится ограничиваться только алгебраическим языком.
Но для двух факторов можно даже не переходить к трехмерному пространству, а ограничиться плоскостью.
Для этого достаточно произвести сечение поверхности отклика плоскостями, параллельными плоскости X1OX2 и полученные в сечениях линии спроектировать на эту плоскость.

Каждая линия соответствует постоянному значению параметра оптимизации. Такая линия называется линией равного отклика.
Полиномиальные модели
Мы представили неизвестную нам функцию отклика полиномом. Операция замены одной функции другой в каком-то смысле эквивалентной функцией называется аппроксимацией. Значит, ми аппроксимировали неизвестную функцию полиномом.
Но полиномы бывают разных степеней. Какой взять на первом шаге?
Эксперимент нужен только для того, чтобы найти численные значения коэффициентов полинома. Поэтому чем больше коэффициентов, тем больше опытов окажется необходимым. А мы стремимся сократить их число. Значит, надо найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявленным к модели. Чем ниже степень полинома при заданном числе факторов, тем меньше в нем коэффициентов.
Мы хотим, чтобы модель хорошо предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называется направлением градиента. Ясно, что движение в этом направлении приведет к успеху быстрее, чем движение в любом другом направлении (это значит, что будет достигнута экономия числа опытов).
Полином первой степени – линейная модель – это то, что нам нужно.
С одной стороны, он содержит информацию о направлении градиента, с другой – в нем минимально возможное число коэффициентов при данном числе факторов. Единственное опасение в том, что неясно, будет ли линейная модель всегда адекватной. Ответ зависит еще и от объекта.
Вопрос в том, как выбрать подобласть в факторном пространстве, чтобы линейная модель оказалась адекватной. Условие аналитичности функции отклика гарантирует нам эту возможность. Всегда существует такая окрестность любой точки (точнее, почти любой точки), в которой линейная модель адекватна.
Размер такой области заранее не известен, но адекватность можно проверять по результатам эксперимента. Значит, выбрав сначала произвольную подобласть, мы, рано или поздно, найдем ее требуемые размеры, И как только это случится, воспользуемся движением по градиенту.
На следующем этапе мы будем искать линейную модель уже в другой подобласти. Цикл повторяется до тех пор, пока движение по градиенту не перестанет давать эффект. Это значит, что мы попали и область, близкую к оптимуму. Такая область называется «почти стационарной». Здесь линейная модель уже не нужна. Либо попаданием в почти стационарную область задача решена, либо надо переходить к полиномам более высоких степеней, например второй степени, чтобы подробнее описать область оптимума.
Удачный выбор подобласти имеет большое значение для успеха всей работы. Он связан с интуитивными решениями, которые принимает экспериментатор на каждом этапе.
Кроме задачи оптимизации, иногда возникает задача построения интерполяционной модели. В этом случае нас не интересует оптимум. Просто мы хотим предсказывать результат с требуемой точностью во всех точках некоторой заранее заданной области. Тут не приходится выбирать подобласть. Необходимо последовательно увеличивать степень полинома до тех пор, пока модель не окажется адекватной. Если адекватной оказывается линейная, или неполная квадратная модель (без членов, содержащих квадраты факторов), то ее построение аналогично тому, что требуется для оптимизации.
2. Дробный факторный эксперимент. Дробная реплика. Выбор полуреплики. Реплики большой дробности.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №26
1.Матричный подход к регрессивному анализу. Матрица дисперсий ковариаций.
Регрессионный анализ. Метод наименьших квадратов (МНК)
Экспериментальное исследование зависимости физических величин, влияния условий на свойства и поведение исследуемых систем и соединений является весьма важной задачей в области химических исследований. Эта задача возникает в самых различных областях химии и позволяет решать многие проблемы, например:
1) Задача построения калибровочных зависимостей, по которым можно прогнозировать значение условий, которые обеспечивают определенный результат.
2) Определение важных физико-химических характеристик системы – например, зависимость свободной энергии системы от температуры будет линейной, а ее наклон равен изменению энтропии системы с отрицательным знаком.
3) Еще одна задача – сжатие (компактизация данных), когда подобранная функция используется для описания (аппроксимации) огромного массива экспериментальных данных (например, зависимость теплоемкости от температуры можно представить в виде функции, и в справочниках приводят не экспериментальную таблицу зависимости Cp от T, а коэффициенты выбранной функции).
4) Аппроксимация экспериментальных данных функцией с целью поиска точек минимума (максимума) – задача оптимизации.
Статистический анализ
Перейдем к статистическому анализу в матричной форме.
Будем предполагать, что постулаты регрессионного анализа выполняются.
Первый постулат. Параметр оптимизации y есть случайная величина с нормальным законом распределения. Дисперсия воспроизводимости – одна из характеристик этого закона распределения.
В данном случае, как и по отношению к любым другим постулатам, нас интересуют два вопроса: как проверить его выполнимость и к чему приводят его нарушения?
При наличии большого экспериментального материала (десятки параллельных опытов) гипотезу о нормальном распределении можно проверить стандартными статистическими тестами (например, χ2– критерием). К сожалению, экспериментатор редко располагает такими данными, поэтому приходится принимать этот постулат на веру.
Второй постулат. Дисперсия y не зависит от абсолютной величины y. Выполнимость этого постулата проверяется с помощью критериев однородности дисперсий в разных точках факторного пространства. Нарушение этого постулата недопустимо.
Всегда существует такое преобразование y, которое делает дисперсии однородными. Увы, его не всегда легко найти. Довольно часто помогает логарифмическое преобразование, с которого обычно начинают поиски.
Третий постулат. Значения факторов суть неслучайные величины. Это несколько неожиданное утверждение практически означает, что установление каждого фактора на заданный уровень и его поддержание существенно точнее, чем сшибка воспроизводимости.
Нарушение этого постулата приводит к трудностям при реализации матрицы планирования. Поэтому оно обычно легко обнаруживается экспериментатором.
Существует еще четвертый постулат, налагающий ограничения на взаимосвязь между значениями факторов. Что значит провести статистический анализ? Это значит проверить ряд статистических гипотез: гипотезу об адекватности заданной модели, гипотезу о значимости отдельных коэффициентов регрессии и др. Фундаментальную роль в анализе уравнения регрессии играет матрица
M–1=(XTX  )–1,
)–1,
которая называется матрицей дисперсий ковариаций. Прямая матрица М называется информационной матрицей Фишера.
В структуре матрицы дисперсий-ковариаций содержится вся информация о статистических свойствах модели. Провести статистический анализ значит извлечь эту информацию. Для этого прежде всего перейдем от матрицы, обратной к матрице системы
нормальных уравнений, к матрице М–1. Оценка дисперсии воспроизводимости  – скаляр; ХТХ – квадратная матрица.
– скаляр; ХТХ – квадратная матрица.
На главной диагонали матрицы-произведения стоят оценки дисперсий коэффициентов регрессии, вне главной диагонали расположены оценки ковариаций.
Ковариация определяется по формуле
 .
.
2. Обоснование выбора матрицы математического планирования эксперимента и критерии его оценки. Математическая модель. Критерий Фишера.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №27
1.Ошибка опыта. Классификация ошибок опыта. Оценка ошибки опыта.
Дата добавления: 2018-04-04; просмотров: 2455; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
