Проверка коэффициентов на значимость
Значимость отдельных коэффициентов уравнения множественной регрессииоценивается с помощью Т-критерия Стьюдента по формуле (4).
, (4)
где 
- оценка 
-го коэффициента модели;
- оценка дисперсии параметра - 
-й элемент главной диагонали дисперсионно-ковариационной матрицы 
, формула (5).
, (5)
где 
- оценка дисперсии ошибки u;
- сумма квадратов ошибок.
Полученное по формуле (4) значение расчётного критерия Стьюдента 
для каждого коэффициента 
сравнивается с табличным (приложение Б) при уровне значимости 
. Если фактическое значение 
превышает табличное, то коэффициент (параметр) модели значим ( 
) с вероятностью 
. Следует принимать число степеней свободы n-k (
-число наблюдений, 
- число коэффициентов модели).
Порядок работы при проверке значимости коэффициента по t-статистике
1. Формулируем нулевую гипотезу Ho о не значимости параметра 
, и альтернативную H1 – о его значимости.
2. Выбираем уровень значимости α (1% или 5%) – максимально допустимой вероятности ошибочного принятия гипотезы H1. Вычисляем число степеней свободы (n-1).
3. По таблицам распределения Стьюдента определяем критическое значение критерия (приложение Б)
4. Если расчётный t-критерий по абсолютной величине больше табличного, то коэффициент является значимым при выбранном уровне значимости α .В противном случае коэффициент незначим (на данном уровне α )
Пример 2.Для уравнения регрессии, полученного в Примере 1., вычислить значение Т-критерия Стьюдента и определить статистическую значимость каждого коэффициента модели 
при уровне значимости 5%.
1. Рассчитаем сумму квадратов ошибок:
RSS = 
= 218,25-218,1875=0,0625.
Тогда 
- оценка дисперсии ошибки u: =0,0625/(4-3)= 0,0625.
2. Рассчитаем дисперсионно- ковариационную матрицу
= (0,0625/1)* 
= 
.
Тогда соответствующие дисперсии коэффициентов
= 
= 
= 0,015625.
Табличное значение (двусторонний) 
.
А расчётные значения t-критериев.
.
.
.
Каждый из коэффициентов значим 
, т.к. больше табличного значения 12,7 при уровне значимости 5%.
Проверка адекватности уравнения множественной регрессии в целом
Значимость уравнения множественной регрессии в целом (
)оценивается с помощью F-критерия Фишера:
, (6)
где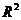 
- коэффициент детерминации - индикатор степени подгонки модели к фактическим данным - или часть вариации (дисперсии) зависимой переменной y, которая объясняется уравнением регрессии. Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем лучше прогноз. Если имеется R-квадрат равный 0.4, то 40% от исходной изменчивости или дисперсии могут быть объяснены, а 60% остаточной изменчивости остаются необъясненными моделью. R-квадрат определяется при помощи формулы (7)
, (7)
- число наблюдений;
k – число коэффициентов факторов;
-среднее значение зависимой переменной.
Полученное по формуле (6) значение F сравнивается с табличным (приложение Б) при уровне значимости . Если фактическое значение F-критерия Фишера превышает табличное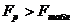 
, то уравнение статистически значимо, т.е. модель адекватна () с вероятностью . Следует принимать число степеней свободы k-1 (по горизонтали), n-k (по вертикали).
Дата добавления: 2018-04-05; просмотров: 523; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!