Математичні основи функціонування елементів
Та вузлів комп’ютерної електроніки
3.1.1. Основні поняття алгебри логіки. Логічна функція. Для опису роботи логічних елементів (ЛЕ) цифрової техніки використовують апарат математичної логіки. Математична логіка це наука про вживання математичних методів для вирішення логічних задач. Для аналізу роботи ЛЕ і схем на їх основі використовують розділ математичної логіки, який називається алгеброю логіки або булевою алгеброю (на ім'я ірландського математика Д. Буля (1815 – 1864 р.)). Алгебру логіки називають також численням висловів. Під висловом розуміють будь-яке твердження, про яке можна сказати, що воно істинне або хибне. Якщо вислів істинний, то його значення приймають рівним одиниці, якщо він хибний, то його значення приймають рівним нулю. Цифри 0 або 1 не виражають кількісних співвідношень і є не числами, а символами, які визначають конкретний стан об’єкту, події, процесу тощо. Ці символи представляють константи булевої алгебри. Їх називають логічною одиницею (лог. 1) та логічним нулем (лог. 0).
Таким чином, значення висловів можна розглядати як змінну величину, що приймає тільки два дискретні значення – 0 або 1. Це приводить до повної відповідності між логічними висловами в математичній логіці і двійковими цифрами в двійковій системі числення, що дозволяє описувати роботу цифрових схем на логічних елементах за допомогою математичного апарату алгебри логіки.
|
|
|
Основними поняттями алгебри логіки є логічна змінна і логічна функція. В загальному випадку логічна змінна може приймати одне з К-значень (К-значна логіка). Перелік всіх символів, які відповідають області значень, називають алфавітом, а самі символи – буквами алфавіту. Логічні змінні позначають буквами латинського алфавіту, наприклад: х1, х2, х3,…; у1, у2, у3,...та іншими. Якщо область значень логічних змінних містить тільки два значення, то такі змінні називаються двійковимиабо булевими, якщо три - трійковими і таке інше. Оскільки в основу сучасної комп’ютерної електроніки покладена двійкова система числення, надалі будемо розглядати тільки двійкові (булеві) змінні, які можуть приймати тільки два значення: х = 0, якщо х ≠ 1 і х = 1, якщо х ≠ 0.
Сукупність значень логічних змінних утворює набори значень, які представляють у вигляді двійкових чисел або їх еквівалентів – вісімкових або десяткових чисел. Наприклад, булевим змінним х1, х2, х3, х4, залежно від значень, прийнятих кожною змінною, відповідають набори: 0000, 0011, 1001, 1101, 1110 та інші. Якщо змінна має тільки два значення, а кількість таких змінних дорівнює n, то загальна кількість наборів дорівнює 2n.
Логічною функцієюабо булевою функцією (БФ) називають функцію, аргументами якої є логічні змінні і яка приймає значення з тієї ж множини, що й самі логічні змінні. Булеві функції або інакше перемикальні функції приймають одне з двох значень 0 або 1. Логічні функції можуть залежати від одного, двох і, взагалі, будь-якого числа аргументівабовхідних змінних. Такі функції позначають наступним чином: f(х), f(х1,х2,… хn), у(х), z(х) тощо. Областю визначення БФ від n-змінних Y = f(х1,х2,…,xi,...,хn) є множина наборів х1х2…xi...хn, які є двійковими словами з довжиною n, де кожний з аргументів xi має значення 0 або 1. Кількість всіляких булевих функцій від n аргументів дорівнює 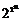 , а областю визначення кожної з цих функцій є сукупність наборів з n-двійкових цифр, загальна кількість яких дорівнює 2n. При збільшенні n кількість БФ швидко зростає: при n=1 вона дорівнює 4; при n=2 - 16; при n=3 - 256; при n=4 - 65536, а при n=5 - 4294966296. Скільки би аргументів n не мала булева функція і яким би складним не був би зв’язок між БФ та її аргументами, таку булеву функцію завжди можна представити у вигляді суперпозиції простих БФ від одного і двох аргументів. До таких функцій, на сам перед слід віднести булеві функції, які у сукупності утворюють так званий булев базис, а саме булеві функції від одного і двох аргументів, які реалізують операції логічного заперечення, логічного додавання та логічно-го множення.
, а областю визначення кожної з цих функцій є сукупність наборів з n-двійкових цифр, загальна кількість яких дорівнює 2n. При збільшенні n кількість БФ швидко зростає: при n=1 вона дорівнює 4; при n=2 - 16; при n=3 - 256; при n=4 - 65536, а при n=5 - 4294966296. Скільки би аргументів n не мала булева функція і яким би складним не був би зв’язок між БФ та її аргументами, таку булеву функцію завжди можна представити у вигляді суперпозиції простих БФ від одного і двох аргументів. До таких функцій, на сам перед слід віднести булеві функції, які у сукупності утворюють так званий булев базис, а саме булеві функції від одного і двох аргументів, які реалізують операції логічного заперечення, логічного додавання та логічно-го множення.
|
|
|
Логічним запереченнямназивають операцію, яка визначає такий зв’язок між логічними змінними х та у, при якому у є істинною, коли х хибна або навпаки, коли у хибна, то х істинна. Цю операцію називають інверсією або доповненням, а також операцією НЕ. Для її позначення використовують риску над відповідними змінними. Булева функція, яка реалізує логічну операцію заперечення - логічне „НЕ” (булева функція НЕ), записується як Y = 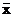 і читається „Y є не х”.
і читається „Y є не х”.
|
|
|
Логічним додаванням змінних x1 та x2 називають операцію, яка дає хибний результат, коли одночасно є хибними обидві змінні x1, x2, а коли хоча б одна з цих змінних є істинною, то результат операції також є істинним. Цю операцію називають операцією АБО, диз’юнкцією, а також логічним додаванням. Для позначення операції диз’юнкція звичайно застосовують символи: „v” чи „+”. Булева функція Y, яка використовує операцію „АБО” (булева функція АБО) записується як Y = х1 v х2 чи Y = х1 + х2, що читається як „Y є х1 або х2”. У загальному випадку диз’юнкція може виконуватися над будь-якою кількістю логічних змінних, в цьому випадку відповідна булева функція „АБО” записується як Y = x1 v x2 v …. v xi v… v xn чи Y = x1 + x2 + …. + xi +… + xn.
|
|
|
Логічним множеннямзмінних x1 та x2 називають операцію, яка є істинною тільки тоді, коли одночасно є істинними логічні змінні x1 та x2, а коли хоча б одна з цих змінних є хибною, то результат операції також є хибним. Цю операцію називають операцією І, кон’юнкцією, а також логічним добутком. Для позначення кон’юнкції звичайно використовують символи „  ” чи „×”.Булева функція Y, яка використовує операцію „І” (булева функція І) записується як Y = х1
” чи „×”.Булева функція Y, яка використовує операцію „І” (булева функція І) записується як Y = х1  х2 чи Y = х1×х2 (допускається також Y = х1х2), що читається як „Y є х1 і х2”. У загальному випадку кон’юнкція може виконуватися над будь-якою кількістю логічних змінних, в цьому випадку булева функція „І” записується у вигляді Y = x1
х2 чи Y = х1×х2 (допускається також Y = х1х2), що читається як „Y є х1 і х2”. У загальному випадку кон’юнкція може виконуватися над будь-якою кількістю логічних змінних, в цьому випадку булева функція „І” записується у вигляді Y = x1  x2
x2  ….
….  xi
xi  …
…  xn чи Y = x1×x2×….×xi×…×xn = x1x2….xi…xn.
xn чи Y = x1×x2×….×xi×…×xn = x1x2….xi…xn.
Часто для задання булевих функцій використовують табличний спосіб. У цьому способі булева функція Y = f(х1,х2,…,xi,...,хn) задається таблицею справжності, в лівій частині якої представлені всі можливі двійкові набори довжиною n, а в правій - значення функції на цих наборах. Таблиці справжності для булевих функцій НЕ (Y = 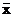 ), АБО (Y = х1 v х2) та І (Y = x1
), АБО (Y = х1 v х2) та І (Y = x1  x2) показані на рис. 3.1
x2) показані на рис. 3.1
| Булева функція НЕ | Булева функція АБО | Булева функція І | ||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||
|
Рис. 3.1. Таблиці справжності булевих функцій НІ, АБО та І | ||||||||||||||||||||||||||||||||||||||
В складних логічних виразах, які містять різноманітні логічні операції встановлено суворий порядок (пріоритет) їх виконання, а саме спочатку виконуються всі операції інверсії, потім операції кон’юнкції і в останню чергу операції диз’юнкції. Операції з однаковим пріоритетом звичайно виконуються послідовно з ліва направо. Якщо необхідно змінити порядок виконання операцій, то в логічних виразах використовують дужки. Операції в дужках виконуються в першу чергу згідно пріоритету згаданому вище.
3.1.2. Основні закони алгебри логіки.Закони алгебри логіки базуються на наступних аксіомах:
х + 0 = х, х×0 = 0, 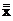 = x;
= x;
х + 1 = 1, х×1 = х;
х + х = х, х×х = х;
х + 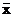 = 1, х×
= 1, х× 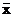 = 0.
= 0.
Нижче наведені без доказів основні закони алгебри логіки, які називають системою рівносильних перетворень.
1. Закон нульової множини
0×х1×х2×...×хn=0. (3.1)
Відповідно до (3.1) кон’юнкція будь-якої кількості змінних дорівнює нулю, якщо хоча б одна з них дорівнює нулю.
2. Закон універсальної множини
1+х1+х2+…+хn=1. (3.2)
Відповідно до (3.2) диз’юнкція будь-якої кількості змінних дорівнює одиниці, якщо хоча б одна з них дорівнює одиниці.
3. Комутативні закони (закони перестановки):
х1×х2×х3 = х2×х1×х3 = х3×х2×х1, (3.3)
х1+х2+х3 = х2+х1+х3 = х3+х2+х1. (3.4)
Відповідно до (3.3), (3.4) результати виконання операцій кон’юнкції і диз’юнкції не залежать від порядку розташування змінних.
4. Асоціативні закони (закони сполучення):
х1×х2×х3 = х1×(х2×х3) = (х1×х2)×х3, (3.5)
х1+х2+х3 =х1+(х2+х3) = (х1+х2)+х3. (3.6)
Відповідно до (3.5), (3.6) при обчисленні логічних виразів з послідовності операцій кон’юнкції або диз’юнкції результат не залежить від порядку виконання операцій кон’юнкції або диз’юнкції над парами змінних.
5. Дистрибутивні закони (розподільні закони):
х1×(х2+х3)=х1×х2+х1×х3, (3.7)
х1+х2×х3 = (х1+х2)×(х1+х3). (3.8)
6. Закони ідемпотентності (тавтології, повторення):
х×х×х×…×х = х, (3.9)
х + х + х +…+ х = х. (3.10)
На підставі закону ідемпотентності можна виділяти змінні, що повторюються, в наслідок чого в булевій алгебрі не мають сенсу показники ступеня і числові коефіцієнти, що відрізняє її від звичайної алгебри.
7. Закон подвійної інверсії
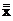 = х, (3.11)
= х, (3.11)
тобто подвійну інверсію можна опустити. Цей закон можна узагальнити на будь-яку парну кількість інверсій.
8. Закони доповнювання:
а) логічна суперечність
х× 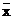 =0, (3.12)
=0, (3.12)
б) виключеного третього
х + 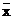 = 1. (3.13)
= 1. (3.13)
9. Закони поглинання:
х1 (х1+х2)×(х1+х3) ×…× (х1+хn)=х1, (3.14)
х1+х1×х2+х1×х3+…+х1×хn=х1. (3.15)
Ці закони випливають з аксіом алгебри логіки і дозволяють замінити декілька членів логічних виразів, які утворюють кон’юнкції (х1+х2)×(х1+х3) ... (х1+хn) або диз’юнкції х1×х2+х1×х3+…+х1×хn, одним членом х1, якщо він входить до цих виразів як співмножник або доданок.
10. Закони склеювання:
х1×х2+х1× 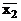 =х1, (3.16)
=х1, (3.16)
(х1+х2)×(х1+ 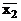 )=х1. (3.17)
)=х1. (3.17)
Ці закони також випливають з аксіом алгебри логіки і дозволяють замінити два члени, що мають однакову загальну частину х1 і аргумент х2 без інверсії в одному члені і з інверсією в іншому, одним членом х1, тобто виконати „склеювання” двох членів.
11. Закони узагальненого склеювання:
х1×х2+ 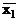 ×х3+х2×х3 = х1×х2 +
×х3+х2×х3 = х1×х2 + 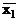 ×х3, (3.18)
×х3, (3.18)
(х1+х2)×( 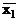 +х3)×(х2+х3) = (х1+х2)×(
+х3)×(х2+х3) = (х1+х2)×( 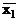 +х3). (3.19)
+х3). (3.19)
12. Закони де Моргана
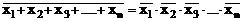 , (3.20)
, (3.20)
 , (3.21)
, (3.21)
тобто інверсія диз’юнкції дорівнює кон’юнкції інверсій, а інверсія кон’юнкцій дорівнює диз’юнкції інверсій.
13. Закон Шеннона (узагальнений закон де Моргана):
 (х1,х2,х3,....,хn,×,+) = f(
(х1,х2,х3,....,хn,×,+) = f( 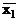 ,
, 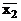 ,
, 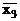 ,...,
,...,  ,+,×), (3.22)
,+,×), (3.22)
тобто для отримання інверсії функції потрібно замінити всі аргументи їх інверсіями, всі знаки кон’юнкції на знаки диз’юнкції і навпаки. Наприклад, якщо f = х1×х2 + х3×х4 + + 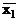 ×х4, то інверсна їй функція
×х4, то інверсна їй функція  = (
= ( 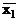 +
+ 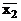 )×(
)×( 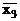 + +
+ + 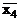 )×(х1 +
)×(х1 + 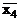 ). Цей закон також має назву принцип подвійності або дуальності.
). Цей закон також має назву принцип подвійності або дуальності.
Перелічені вище закони можна довести методом індукції, тобто перевіркою їх для всіх можливих комбінацій значень логічних змінних. Ці закони можна також довести аналітично на основі інших законів і аксіом алгебри логіки. Наприклад, ідемпотентність диз’юнкції доводиться наступними перетвореннями: х + х = (х + х)×1=(х + х )×(х + 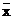 ) = х + х×
) = х + х× 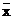 = х + 0 = х. Відзначимо, що знак рівності у формулах алгебри логіки не має кількісного сенсу і фактично означає рівнозначність функцій в лівій і правій частинах формул. Дві функції називають рівнозначними, якщо при будь-яких значеннях аргументів вони приймають однакові значення.
= х + 0 = х. Відзначимо, що знак рівності у формулах алгебри логіки не має кількісного сенсу і фактично означає рівнозначність функцій в лівій і правій частинах формул. Дві функції називають рівнозначними, якщо при будь-яких значеннях аргументів вони приймають однакові значення.
3.1.3. Способи задання булевих функцій.Задання булевої функції від n аргументів - це визначення її значень на всіх 2n наборах. В алгебрі логіки існують булеві функції, значення яких можуть бути невизначеними на деяких наборах, тобто на таких наборах БФ може приймати довільні значення. В цьому випадку булеву функцію називають частково визначеною.
Для задання булевих функцій найчастіше використовують матричний (табличний) та аналітичний способи.
Як згадувалось вище, табличний спосіб задання БФ полягає в складанні таблиці справжності. Кількість рядків такої таблиці дорівнює кількості наборів 2n, на яких визначена булева функція від n змінних, а кількість стовпців дорівнює n + 1. Перші n стовпці позначають символами аргументів, тобто логічних змінних, від яких залежить функція, а (n+1)-й стовпець - символом самої БФ. В кожному рядку таблиці справжності записують набір та відповідне йому значення булевої функції. Нижче (табл. 3.1) наведено приклад таблиці справжності для двох булевих функцій від трьох аргументів: Y = Y(х1,х2,х3) і Z = Z(х1,х2,х3).
З таблиці 3.1 випливає, що функція Y повністю визначена, а функція Z частково визначена (невизначені для неї значення вказані символом „-”). Таблиці справжності представлені у такому вигляді називають одновходовими і застосовують для задання булевих функцій від невеликої кількості аргументів. При великій кількості аргументів n кількість наборів 2n буде великою і одновходова таблиця справжності стає громіздкою.
Таблиця 3.1
Таблиця справжності булевих функцій Y та Z
| х1 | x2 | x3 | Y | Z |
| 0 0 0 | 1 | 0 | ||
| 0 0 1 | 0 | 1 | ||
| 0 1 0 | 1 | - | ||
| 0 1 1 | 0 | 1 | ||
| 1 0 0 | 1 | - | ||
| 1 0 1 | 1 | 0 | ||
| 1 1 0 | 0 | - | ||
| 1 1 1 | 0 | 1 | ||
Коли кількості аргументів велика, застосовують більш компактні двохвходові таблицісправжності. Для їх побудови аргументи БФ розділяють на дві приблизно рівні за кількістю аргументів групи. У групах використовують всі можливі набори аргументів, що включені до групи. Рядки таблиці позначають наборами однієї групи, а стовпці - наборами іншої групи. Кожна клітка таблиці відповідає одному двійковому набору і в ній записують відповідне значення БФ. Прикладом двохвходової таблиці справжності для функції Y = Y(х1,х2,х3) з таблиці 3.1 є таблиця 3.2.
Таблиця 3.2
Двохвходова таблиця справжності булевої функції Y
| х1 | х2 х3 | |||
| 00 | 01 | 10 | 11 | |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
У багатьох випадках більш зручним є не табличний, а аналітичний спосіб задання булевих функцій у вигляді алгебраїчних формул. Тим більше, що ці способи взаємно зв’язані між собою оскільки є можливість переходу від одного з них до іншого. Найбільш раціональним є представлення булевих функцій в так званих нормальних формах, в основу яких покладені поняття елементарної кон’юнкції та елементарної диз’юнкції.
Елементарна кон’юнкція це логічний добуток декількох аргументів булевої функції, в який кожен з цих аргументів входить одноразово із знаком інверсії або без нього.Прикладами елементарних кон’юнкцій є логічні добутки: х1х2, х1х3х4, х2 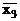 х4.
х4.
Елементарна диз’юнкція це логічна сума декількох аргументів булевої функції, в яку кожен з цих аргументів входить одноразово із знаком інверсії або без нього. Прикладами елементарних диз’юнкцій є логічні суми: х1+х2, х1+ 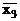 , х1+х2+
, х1+х2+ 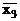 .
.
Якщо булева функція представлена через основні операції алгебри логіки: інверсію, кон’юнкцію та диз’юнкцію, то таку форму її задання називають нормальною. Розрізняють диз’юнктивну та кон’юнктивну нормальні форми запису БФ.
Диз’юнктивною нормальною формою (ДНФ) називають таку форму запису БФ, яка є логічною сумою елементарних кон’юнкцій. Прикладом ДНФ може бути такий запис БФ: 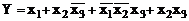 .
.
Кон’юнктивною нормальною формою(КНФ) називають таку форму запису БФ, яка є логічним добутком елементарних диз’юнкцій. Прикладом КНФ може бути такий запис БФ: Y = х1(х2 + 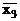 )(
)( 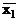 +
+ 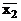 +x3)(х2+х3).
+x3)(х2+х3).
Будь-яка довільна булева функція, яка задана аналітичним способом, може бути зведена до ДНФ або КНФ шляхом перетворень з використанням законів і аксіом алгебри логіки, наведених в 3.1.2.
Очевидно, що одна й та ж сама БФ може бути задана множиною різних КНФ і ДНФ. Проте існують універсальні види цих форм, які застосовують для аналітичного завдання булевих функцій. Такі форми пов’язані з рангомелементарної диз’юнкції або кон’юнкції, під яким розуміють число їх аргументів. Якщо до складу логічної формули входять елементарні кон’юнкцій однакового рангу, які зв’язані між собою операцією диз’юнкції, то така форма завдання булевої функції буде єдиною і її називають досконалою диз'юнктивною нормальною формою (ДДНФ) або канонічною сумою мінтермівабо ще стандартною сумою. Інакше ДНФ називають досконалою, якщо кожен її член від n аргументів булевої функції містить всі n аргументів.
Будь-яку функцію, що задана в ДНФ, можна представити в ДДНФ. Цю операцію перетворення ДНФ в ДДНФ називають розгортанням. Для розгортання в кожну елементарну кон’юнкцію шляхом множення її на (х + 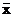 ) = 1 вводять відсутню в ній змінну, розкривають дужки та позбуваються однакових кон’юнкцій, використовуючи закон ідемпотентності (3.9). Пояснимо суть операції розгортання на прикладі функції
) = 1 вводять відсутню в ній змінну, розкривають дужки та позбуваються однакових кон’юнкцій, використовуючи закон ідемпотентності (3.9). Пояснимо суть операції розгортання на прикладі функції 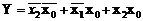 :
:

Досконалою кон’юнктивною нормальною формою (ДКНФ) булевої функції називають таке її аналітичне задання, коли воно містить набори елементарних диз’юнкцій однакового рангу, зв’язаних кон’юнкцією. Таке аналітичне задання БФ є єдиним і його називають також канонічним добутком макстермівабо стандартним добутком сум. Інакше, КНФ називають досконалою якщо кожний її член від n аргументів булевої функції містить всі n аргументи.
Будь-яку булеву функцію, задану в КНФ можна розгорнути в ДКНФ. Для цього в кожну диз’юнкцію шляхом додавання до неї x 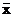 =0 вводять відсутні аргументи БФ, виконують перетворення, використовуючи дистрибутивний (3.8) і комутативний (3.4) закони, і за допомогою закону ідемпотентності (3.9) позбуваються однакових диз’юнкцій. Пояснимо це на прикладі функції Y = (x2 + x0)×(x1 + +
=0 вводять відсутні аргументи БФ, виконують перетворення, використовуючи дистрибутивний (3.8) і комутативний (3.4) закони, і за допомогою закону ідемпотентності (3.9) позбуваються однакових диз’юнкцій. Пояснимо це на прикладі функції Y = (x2 + x0)×(x1 + + 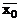 )×(
)×( 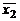 +
+ 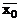 ):
):

В алгебрі логіки використовують особливі логічні функції, які називають конституентою одиниці і конституентою нуля. Конституента одиниці - це логічна функція від n аргументів, яка приймає значення одиниці тільки на одному наборі аргументів і дорівнює 0 на всіх інших 2n-1 наборах. Конституента нуля - це логічна функція від n аргументів, яка приймає значення нуля тільки на одному наборі аргументів і дорівнює одиниці на всіх інших 2n-1 наборах. Нескладно зрозуміти, що логічною функцією, яка є конституентою одиниці може бути будь-яка елементарна кон’юнкція. Наприклад, кон’юнкція 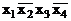 приймає значення, яке дорівнює 1 тільки на наборі 1010, на всіх інших 24 – 1 = 15 наборах, завдяки тому, що хоча би один член кон’юнкції буде дорівнювати 0, вона обертається в нуль (закон нульової множини (3.1)). Таким же чином конституентою нуля може бути логічна функція, яка є елементарною диз’юнкцією. Дійсно, наприклад, диз’юнкція
приймає значення, яке дорівнює 1 тільки на наборі 1010, на всіх інших 24 – 1 = 15 наборах, завдяки тому, що хоча би один член кон’юнкції буде дорівнювати 0, вона обертається в нуль (закон нульової множини (3.1)). Таким же чином конституентою нуля може бути логічна функція, яка є елементарною диз’юнкцією. Дійсно, наприклад, диз’юнкція  приймає значення 0 тільки на наборі 010, на всіх інших 23 – 1= 7 наборах вона дорівнює 1 за рахунок того, що для таких наборів хоча б один член диз’юнкції дорівнює одиниці (закон універсальної множини (3.2)).
приймає значення 0 тільки на наборі 010, на всіх інших 23 – 1= 7 наборах вона дорівнює 1 за рахунок того, що для таких наборів хоча б один член диз’юнкції дорівнює одиниці (закон універсальної множини (3.2)).
Поняття конституент одиниці і нуля використовують для аналітичного запису булевих функцій в ДДНФ та ДКНФ безпосередньо з таблиць справжності БФ. В цьому випадку з метою отримання ДДНФ в таблиці справжності виділяють набори, на яких логічна функція має одиничні значення. Для кожного такого набору записують елементарну кон’юнкцію аргументів функції, при цьому аргументи, які в наборі мають одиничні значення записують в кон’юнкції без інверсії, а ті, що мають нульові значення, з інверсією. Очевидно, що отримані таким чином елементарні кон’юнкції є конституентами одиниці. ДДНФ булевої функції записують, як логічну суму всіх її конституент одиниці. Для запису логічної функції в ДКНФ поступають так само. Виділяють в таблиці справжності набори, на яких БФ дорівнює нулю. Кожен з цих наборів записують як диз’юнкцію аргументів функції, при цьому аргументи набору, які мають нульові значення, записують без інверсії, а ті, що мають одиничне значення, з інверсією. Оскільки отримані таким чином елементарні диз’юнкції є конституентами нуля, ДКНФ булевої функції записують як логічний добуток всіх її конституент нуля.
Для ілюстрації описаного вище способу отримання ДДНФ і ДКНФ безпосередньо з таблиці справжності булевої функції розглянемо функцію Y, задану табл. 3.1. Як видно з табл. 3.1, булева функція Y(x1,x2,x3) приймає значення, які дорівнюють одиниці на наборах 000, 010, 100, 101, яким відповідають елементарні кон’юнкції  ,
, 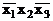 ,
, 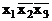 ,
,  , які є конституентами одиниці, тому ДДНФ функції Y(x1,x2,x3) можна записати як
, які є конституентами одиниці, тому ДДНФ функції Y(x1,x2,x3) можна записати як
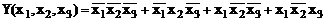 . (3.23)
. (3.23)
Для запису функції Y(x1,x2,x3) в ДКНФ в табл. 3.1 виділяємо набори, на яких ця функція має нулеві значення: 001, 011, 110, 111. Їм відповідають елементарні диз’юнкції 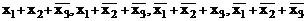 , які є конституентами нуля, тому ДКНФ функції Y(x1,x2,x3) можна записати у вигляді:
, які є конституентами нуля, тому ДКНФ функції Y(x1,x2,x3) можна записати у вигляді:
 . (3.24)
. (3.24)
Зазначимо, що елементарні кон’юнкції ДДНФ - конституенти одиниці називають також мінтермами. Отже, ДДНФце диз’юнкція всіх конституент одиницібулевої функції або диз’юнкція всіх її мінтермів, що відповідають наборам, на яких, згідно таблиці справжності, БФ приймає одиничне значення. Конституенту нуля називають також макстермом. Отже, ДКНФ це кон’юнкція конституент нуляабокон’юнкція макстермів, які відповідають всім наборам з нульовими значеннями функціїтобтоДКНФ є канонічним добутком макстермів.
З властивостей операцій логічного множення і додавання випливає, що сумарна кількість мінтермів (конституент одиниці) і макстермів (конституент нуля) N для будь-якої булевої функції співпадає з числом наборів її аргументів, тобто якщо БФ має n аргументів, то N=2n. Звичайно, якщо кількості наборів аргументів БФ, на яких вона приймає одиничне значення, перевищує кількість наборів, на яких булева функція має нульове значення, то віддають перевагу аналітичному запису БФ в ДКНФ, при зворотному співвідношенні кількостей наборів, булеву функцію зручніше представляти в ДДНФ.
Відзначимо, що аналітичний спосіб завдання функцій алгебри логіки є більш зручним і тому йому часто віддають перевагу порівняно з табличним при аналізі і синтезі елементів та вузлів комп’ютерної електроніки.
3.1.4. Елементарні логічні функції. Будь-яку логічну функцію, яка залежить від n > 2 змінних, можна виразити через суперпозицію булевих функцій одного і двох аргументів. Тому такі БФ мають особливе значення в алгебрі логіки. Їх називають елементарними логічними функціями. Розглянемо ці функції більш докладніше.
В таблиці 3.3 представлені всі можливі 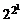 = 4 булеві функції fi(х) одного аргументу. Функції f1(х) =
= 4 булеві функції fi(х) одного аргументу. Функції f1(х) = 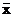 х= 0 та f4(х) = х +
х= 0 та f4(х) = х + 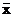 = 1 фактично не залежать від аргументу х, тому їх називають сталими функціями. Перша з них має назву тотожний нуль або константа 0, друга – тотожна одиниця або константа 1. Значення функції f2(х) = х співпадає із значеннями аргументу х, тому її називають функцією тотожностіабоповторення. Функція f3(х) =
= 1 фактично не залежать від аргументу х, тому їх називають сталими функціями. Перша з них має назву тотожний нуль або константа 0, друга – тотожна одиниця або константа 1. Значення функції f2(х) = х співпадає із значеннями аргументу х, тому її називають функцією тотожностіабоповторення. Функція f3(х) = 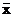 є інверсією аргументу, тобто вона реалізує логічну операцію заперечення і тому є неодноразово згаданою вище булевою функцією запереченняабофункцією НЕ. Відзначимо, що кожна з перелічених вище функцій одного аргументу має інверсну до себе функцію, а саме: f1(х) =
є інверсією аргументу, тобто вона реалізує логічну операцію заперечення і тому є неодноразово згаданою вище булевою функцією запереченняабофункцією НЕ. Відзначимо, що кожна з перелічених вище функцій одного аргументу має інверсну до себе функцію, а саме: f1(х) =  4(х); f4(х) =
4(х); f4(х) =  1(х); f2(х) =
1(х); f2(х) =  3(х); f3(х) =
3(х); f3(х) =  2(х).
2(х).
Таблиця 3.3
Елементарні логічні функції одного аргументу
| fі(х) | х | Алгебраїчний вираз функції | Назва функції | |
| 0 | 1 | |||
| f1(х) | 0 | 0 | х× 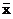
| Тотожний нуль |
| f (х) | 0 | 1 | х | Повторення х |
| f 3(х) | 1 | 0 | 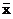
| Заперечення х |
| f 4(х) | 1 | 1 | x + 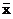
| Тотожна одиниця |
В таблиці 3.4 представлені всі можливі 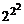 = 16 булеві функції fi(х1,x2) двох аргументів. Таблиця містить таблиці справжності для цих функцій, алгебраїчні вирази функцій в канонічних формах ДДНФ або ДКНФ, а також спрощені за допомогою аксіом і законів алгебри логіки вирази.
= 16 булеві функції fi(х1,x2) двох аргументів. Таблиця містить таблиці справжності для цих функцій, алгебраїчні вирази функцій в канонічних формах ДДНФ або ДКНФ, а також спрощені за допомогою аксіом і законів алгебри логіки вирази.
Так алгебраїчний вираз для функції f1(х1,x2), записаної в ДКНФ, за допомогою закону склеювання (3.17) набуває вигляд f1(х1,x2) = х1 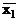 = 0, тобто функція f1(х1,x2) не залежить від змінних х1 і х2 і тотожно дорівнює нулю, тому вона має назву тотожний нуль або константа 0.
= 0, тобто функція f1(х1,x2) не залежить від змінних х1 і х2 і тотожно дорівнює нулю, тому вона має назву тотожний нуль або константа 0.
Функція f2(х1,x2), яка є конституентою одиниці являє собою кон’юнкцію аргументів х1, x2, тобто є булевою функцією І.
Функції f3(х1,x2) і f5(х1,x2) називають відповідно заборона x2 і заборона х1 або запереченням імплікації х2 (функції f14(х1,x2)) і запереченням імплікації х1 (функції f12(х1,x2)). Функція f3(х1,x2) завжди дорівнює нулю, коли х2 = 1 і повторює значення х1, коли х2 = 0. Функція f5(х1,x2) дорівнює нулю при х1=1 і повторює значення х2 при х1=0.
Функція f4(х1,x2) = х1 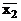 +х1х2, яка задана у ДДНФ, за допомогою (3.16) перетворюється до f4(х1,x2) = х1, тобто реалізує повторення x1.
+х1х2, яка задана у ДДНФ, за допомогою (3.16) перетворюється до f4(х1,x2) = х1, тобто реалізує повторення x1.
Функція f6(х1,x2) = 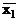 х2+х1х2 подібна до функції f4(х1,x2). За допомогою (3.16) вона перетворюється до f6(х1,x2) = х2, тобто реалізує повторення x2.
х2+х1х2 подібна до функції f4(х1,x2). За допомогою (3.16) вона перетворюється до f6(х1,x2) = х2, тобто реалізує повторення x2.
Функція f7(х1,x2) = 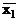 х2+х1
х2+х1 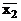 дорівнює одиниці тільки в тому випадку, коли значення її аргументів х1 і х2 неоднакові. Враховуючи цю властивість, функцію f7(х1,x2) називають функцією нерівнозначності або нееквівалентності. Вона також має назви виключальне АБО та сума за модулем 2.
дорівнює одиниці тільки в тому випадку, коли значення її аргументів х1 і х2 неоднакові. Враховуючи цю властивість, функцію f7(х1,x2) називають функцією нерівнозначності або нееквівалентності. Вона також має назви виключальне АБО та сума за модулем 2.
Таблиця 3.4
Елементарні логічні функції двох аргументів
| Набори змінних | Алгебраїчний вираз функцій | Назва функцій | ||||
| х1 | 0 | 0 | 1 | 1 | ||
| х2 | 0 | 1 | 0 | 1 | ||
| f1(х1,x2) | 0 | 0 | 0 | 0 | (х1+х2)(х1+  )×
×( )×
×(  +х2)( +х2)(  + +  ) =
= х1 ) =
= х1  = 0 = 0
| Тотожний 0 |
| f2(х1,x2) | 0 | 0 | 0 | 1 | х1х2 | Кон’юнкція, І |
| f3(х1,x2) | 0 | 0 | 1 | 0 | х1 
| Заборона х2 |
| f4(х1,x2) | 0 | 0 | 1 | 1 | х1  +х1х2 = x1 +х1х2 = x1
| Повторення х1 |
| f5(х1,x2) | 0 | 1 | 0 | 0 |  х2 х2
| Заборона х1 |
| f6(х1,x2) | 0 | 1 | 0 | 1 |  х2+х1х2 = х2 х2+х1х2 = х2
| Повторення х2 |
| f7(х1,x2) | 0 | 1 | 1 | 0 |  х2+х1 х2+х1  = = 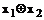
| Сума за моду-лем 2, виклю-чальне АБО |
| f8(х1,x2) | 0 | 1 | 1 | 1 |  х2+х1 х2+х1  +х1х2 =
= x1+x2 +х1х2 =
= x1+x2
| Диз’юнкція, АБО |
| f9(х1,x2) | 1 | 0 | 0 | 0 |   = = 
| Стрілка Пірса, НЕ АБО (АБО-НЕ) |
| f10(х1,x2) | 1 | 0 | 0 | 1 |   +х1х2 = +х1х2 = 
| Еквівалентність |
| f11(х1,x2) | 1 | 0 | 1 | 0 |   +х1 +х1  = = 
| Інверсія х2 |
| f12(х1,x2) | 1 | 0 | 1 | 1 |   +х1 +х1  +х1х2 =
= х1+ +х1х2 =
= х1+ 
| Імплікація х1 |
| f13(х1,x2) | 1 | 1 | 0 | 0 |   + +  х2 = х2 = 
| Інверсія х1 |
| f14(х1,x2) | 1 | 1 | 0 | 1 |   + +  х2+х1х2 =
= х2+х1х2 =
=  +х2 +х2
| Імплікація х2 |
| f15(х1,x2) | 1 | 1 | 1 | 0 |   + +  х2+х1 х2+х1  =
= =
= 
| Штрих Шеффе-ра, НЕ І (І-НЕ) |
| f16(х1,x2) | 1 | 1 | 1 | 1 |   + +  х2+х1 х2+х1  +
+х1х2 = +
+х1х2 =  + х1 = 1 + х1 = 1
| Тотожна 1 |
Функція f8(х1,x2) =  х2+х1
х2+х1  +х1х2, записана в ДДНФ, за допомогою (3.16) і аксіоматичного співвідношення х1+
+х1х2, записана в ДДНФ, за допомогою (3.16) і аксіоматичного співвідношення х1+  х2 = х1+х2 може бути приведена до вигляду f8(х)= х1+ х2, тобто є булевою функцією АБО.
х2 = х1+х2 може бути приведена до вигляду f8(х)= х1+ х2, тобто є булевою функцією АБО.
Функція f9(х1,x2) = 
 при використанні закону де Моргана (3.20) перетворюється до вигляду f9(х1,x2) =
при використанні закону де Моргана (3.20) перетворюється до вигляду f9(х1,x2) =  . Вона є запереченням диз’юнкції і має назви: стрілка Пірса, а також НЕ АБО чи АБО-НЕ.
. Вона є запереченням диз’юнкції і має назви: стрілка Пірса, а також НЕ АБО чи АБО-НЕ.
Функція f10(х1,x2) дорівнює одиниці тільки тоді, коли обидва її аргументи х1 і х2 мають однакові значення, тому її називають функцією рівнозначності або еквівалентності. Якщо виконати інверсію цієї функції і використати відповідні закони алгебри логіки, то отримаємо вираз:
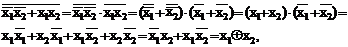
з якого випливає, що функція рівнозначності є інверсією функції нерівнозначності або запереченням суми за модулем два.
Функція f11(х1,x2) = 
 + х1
+ х1  при використанні дистрибутивного закону (3.7) і співвідношення х+
при використанні дистрибутивного закону (3.7) і співвідношення х+ 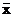 = 1 перетворюється у f11(х1,x2) =
= 1 перетворюється у f11(х1,x2) =  , тобто є інверсією х2.
, тобто є інверсією х2.
Функцію f12(х1,x2) = 
 +х1
+х1  +х1х2 при використанні законів ідемпотентності (3.10) і склеювання (3.16) можна перетворити так: f12(х1,x2) =
+х1х2 при використанні законів ідемпотентності (3.10) і склеювання (3.16) можна перетворити так: f12(х1,x2) = 
 +х1
+х1  +х1х2 =
+х1х2 = 
 + + х1
+ + х1  + х1х2 + х1
+ х1х2 + х1  =
=  (
(  +х1) + х1(х2+
+х1) + х1(х2+  ) = х1+
) = х1+  . Ця функція дорівнює нулю тільки на наборі 01, тобто тісно пов’язана з ним. Така функція має назву імплікаціях1.
. Ця функція дорівнює нулю тільки на наборі 01, тобто тісно пов’язана з ним. Така функція має назву імплікаціях1.
Функція f13(х1,x2) = 
 +
+  х2 =
х2 =  (
(  + х2) =
+ х2) =  є інверсією х1.
є інверсією х1.
Функція f14(х1,x2) = 
 +
+  х2+х1х2 подібним, як і для функції f12(х1,x2) перетворенням, можна привести до виразу f14(х1,x2) =
х2+х1х2 подібним, як і для функції f12(х1,x2) перетворенням, можна привести до виразу f14(х1,x2) =  +х2, тобто вона є імплікацією х2.
+х2, тобто вона є імплікацією х2.
Функція f15(х1,x2) = 
 +
+  х2+х1
х2+х1  =
= 
 + +
+ +  х2+х1
х2+х1  +
+ 
 =
=  (
(  +х2)+
+х2)+  (
(  +х1) =
+х1) =  +
+  =
= 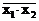 є інверсією кон’юнкції, тобто функцією НЕ І чи І-НЕ, її називають також штрих Шеффера, або заперечення кон’юнкції.
є інверсією кон’юнкції, тобто функцією НЕ І чи І-НЕ, її називають також штрих Шеффера, або заперечення кон’юнкції.
Функція f16(х1,x2)= 
 +
+  х2+х1
х2+х1  +х1х2 =
+х1х2 =  (х2+
(х2+  )+х1(
)+х1(  +х2)=
+х2)=  +х1=1 тотожно дорівнює одиниці, тобто є одиничною постійною функцією, яка має назву тотожна 1.
+х1=1 тотожно дорівнює одиниці, тобто є одиничною постійною функцією, яка має назву тотожна 1.
З перелічених вище 16 функцій двох аргументів дві (f1(х1,x2), f16(х1,x2)) є константами, чотири (f4 (х1,x2), f6(х1,x2), f11(х1,x2), f13(х1,x2)) - фактично функціями однієї змінної. Функції f3(х1,x2), f5(х1,x2), і так само f12(х1,x2), f14(х1,x2) відрізняються тільки порядком використання операції заперечення для аргументів х1 і х2. Отже, є тільки 8 оригінальних функцій двох аргументів: кон’юнкція f2(х1,x2), заборона f3(х1,x2), f5(х1,x2), сума за модулем 2 f7(х1,x2), диз’юнкція f8(х1,x2), стрілка Пірса f9(х1,x2), еквівалентність f10(х1,x2), імплікація f12(х1,x2), f14(х) та штрих Шеффера f15(х1,x2).
3.1.5. Функціонально повні системи булевих функцій. Будь-які функції алгебри логіки можуть бути представлені через інші булеві функції. Таке представлення БФ можливе, завдяки існуванню в алгебрі логіки принципу суперпозиції, який полягає в заміні одних аргументів заданої функції іншими. Наприклад, якщо аргументи функції Y(х, z) у свою чергу є функціями інших аргументів Х(а, b) і Z(с, d), то функція Y(х, z) може бути представлена як Y(a, b, c, d). Зрозуміло, що це є правомірним завдяки тому, що співпадають області значень логічних змінних. Будемо називати функцію fn+1(х), одержану з функцій f1(х), f2(х),…, fn(х) шляхом суперпозиції, суперпозицією цих функцій. На підставі принципу суперпозиції можна встановити зв’язок між БФ. При цьому важливим є склад елементарних логічних функцій, на підставі яких можна побудувати довільну БФ, що має кінцеве число аргументів.
Система логічних функцій F= {f1(х), f2(х), …, fn(х)}, називається функціонально повною, якщо будь-яка функція алгебри логіки може бути представлена за допомогою суперпозицій функцій, які входять до системи F. Таку систему БФ називають базисом. Функціонально повна система логічних функцій називається нескоротноюабо мінімальною, якщо видалення з неї хоча б однієї функції перетворює її на неповну систему.Якщож при видаленні з системи функцій якої-небудь функції ця система не втрачає повноту, то така система функцій називається надлишковою.Критерії для знаходження ознак функціональної повноти довільної системи булевихфункцій в алгебрі логіки встановлює теорема Поста-Яблонського.Аналіз булевих функцій двох змінних на основі вимог цієї теореми приводить до висновку про існування великої кількості різних функціонально повних систем елементарних логічних функцій. До таких систем функцій, наприклад, відносяться: {І, АБО, НЕ}, яку називають булевим базисом; {І, сума за модулем 2, константа - логічна одиниця}, яку називають базисом Жегалкіна; {І-НЕ}, {АБО-НЕ}, так звані монофункціональні базиси; а також системи {І, НЕ }, {АБО, НЕ} та інші. Ці функціонально повні системи БФ є мінімальними. Серед перелічених вище функціонально повних систем больових функцій слід відзначити системи {І-НЕ}, {АБО-НЕ}, які містять тільки одну логічну функцію. Такі функції називаютьуніверсальними логічними функціями.
З позицій алгебри логіки всі функціонально повні системи булевих функцій є рівноцінними. Вибір для використання в цифровій електроніці тієї чи іншої системи переважно залежить від технічних можливостей її реалізації. З цієї точки зору перевагу віддають системам: {І, АБО, НЕ}; {І, НЕ}; {АБО, НЕ}; {І-НЕ}; {АБО-НЕ}. Зазначимо, що в сучасній комп’ютерній схемотехніці переважно використовуються функціонально повні системи БФ, які належать до монофункціональних базисів {І-НЕ} та {АБО-НЕ}.
3.1.6. Мінімінізація логічних функцій.В комп’ютер-ній електроніці будь-яка логічна функція реалізується якою-небудь конкретною електронною схемою. При цьому рівносильні логічні функції, які описуються однаковою таблицею справжності, але представлені різними за складністю аналітичними виразами, вимагають для своєї реалізації різних за технічною комплектацією електронних схем. У зв’язку з цим виникає потреба привести аналітичний виразу бульової функції до вигляду, який вимагає більш простого технічного розв’язання. Іноді визначальним критерієм може бути не простота електронної схеми, а мінімум її вартості, максимальна швидкодія, мінімальна площа, яку схема займає на кристалі, мінімальний набір елементів схеми тощо.
Процес приведення аналітичного виразу БФ до вигляду, що задовольняє заданому критерію мінімінізації, називається мінімінізацією логічних функцій.
В загальному випадку проблема мінімінізації булевих функцій не вирішена до теперішнього часу. Тому не існує методів, які б дозволяли стандартними прийомами визначити вид формули для логічної функції, що задовольняв би тому чи іншому критерію мінімінізації. Методи мінімінізації розробляються окремо для кожної функціонально повної системи БФ. Найбільш повно такі методи розроблені для булевого базису, який складається з булевих функцій диз’юнкції, кон’юнкції та інверсії. При цьому мінімізація БФ зводиться до знаходження такого її аналітичного виразу, який містить мінімальну кількість елементарних булевих функцій: АБО, І, НЕ.
Задача мінімізації булевої функції, що представлена у вигляді ДНФ або КНФ, розв’язується у два етапи: на першому з них знаходять таку форму аналітичного виразу для ДНФ (КНФ), в якому кон’юнкції (диз’юнкції) містять мінімальну кількість змінних, на другому етапі шукають вираз ДНФ (КНФ) з мінімальною кількістю різних елементарних кон’юнкцій (диз’юнкцій). Кінцева мета такого роз-в’язання полягає в пошуку аналітичного виразу для ДНФ (КНФ) булевої функції, який має мінімальну довжину, тобто містить мінімальну загальну кількість змінних (букв).
Розрізняють аналітичні і табличні методи мінімінізації.
Суть аналітичних методівполягає в перетворенні на підставі певних правил аналітичного виразу БФ до вигляду, який відповідає деякому критерію мінімінізації. Серед аналітичних методів мінімінізації найбільш поширеним є метод безпосередніхтотожних перетворень аналітичного виразу булевої функції до мінімальної довжини з використанням законів, аксіом і правил алгебри логіки. Розглянемо цей метод на наступному прикладі.
Необхідно спростити аналітичний вираз булевої функції Y(х1,х2,х3,х4) = х1  +
+  х4+х2х4+х3. Це можна зробити, якщо використати закон дистрибутивності (3.7) і закон де Моргана (3.20): Y(х1,х2,х3,х4) = х1
х4+х2х4+х3. Це можна зробити, якщо використати закон дистрибутивності (3.7) і закон де Моргана (3.20): Y(х1,х2,х3,х4) = х1 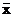 2 + х4(
2 + х4( 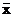 1+ х2) + х3 = х1
1+ х2) + х3 = х1 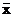 2 +
2 + 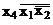 + х3 та застосувати до перших двох доданків аксіоматичне правило х1 +
+ х3 та застосувати до перших двох доданків аксіоматичне правило х1 + 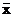 1х2 = х1+ х2. Як результат одержимо
1х2 = х1+ х2. Як результат одержимо
Y(х1,х2,х3,х4)=х1 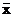 2 +х4+х3.
2 +х4+х3.
Метод безпосередніх перетворень відрізняється відносною простотою і дає добрі результати для нескладних аналітичних виразів БФ. Але цей метод не дозволяє сформулювати чітких правил для одержання бажаного результату, тому кінцевий аналітичний вираз БФ може виявитися не мінімальним.
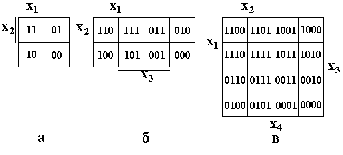
Процесу безпосередніх перетворень можна надати більшої продуктивності при виконанні перетворень за наступною схемою. На першому етапі аналітичний вираз для БФ приводять до ДДНФ. Далі в ДДНФ виявляють елементарні кон’юнкції, які різняться одним членом. Такі кон’юнкції називають сусідніми. До сусідніх кон’юнкцій застосовують закон склеювання (3.16), внаслідок чого їх ранг знижується на одиницю. Наприклад, х1 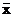 2х3+х1х2х3 = х1х3. Кон’юнкції, одержані як результат склеювання називають імплікантами. Імпліканти одержані після першого склеювання при нагоді склеюють вдруге і так до тих пір, поки склеювання стає неможливим. Імпліканти, які не склеюються, називають простими імплікантами.
2х3+х1х2х3 = х1х3. Кон’юнкції, одержані як результат склеювання називають імплікантами. Імпліканти одержані після першого склеювання при нагоді склеюють вдруге і так до тих пір, поки склеювання стає неможливим. Імпліканти, які не склеюються, називають простими імплікантами.
Диз’юнкцію всіх простих імплікант називають скороченою диз’юнктивноюнормальною формою. Ця форма для даної булевої функції є єдиною. Серед простих імплікант можуть бути такі, які покриваються сукупностями інших імплікант і тому є надлишковими. Після видалення надлишкових імплікант приходять до тупикової диз’юнктивної нормальної форми (ТДНФ). В загальному випадку логічна функція може бути представлена однією або декількома ТДНФ. Ту ТДНФ, яка має найменшу кількість букв (аргументів БФ і їх інверсій) називають мінімальною диз’юнктивною нормальною формою (МДНФ).
Перетворення аналітичного виразу для булевої функцій, подібне описаному вище для БФ заданої у ДДНФ, можливе також для випадку, коли БФ задана у ДКНФ. Відмінність такого перетворення полягає у використанні замість імплікант імпліцент, які є елементарними диз’юн-кціями, одержаними шляхом склеюванням згідно (3.17). Результатом перетворень є мінімальна кон’юнктивна нормальна форма (МКНФ) інверсна до МДНФ.
Для полегшення процедури мінімінізації булевих функцій розроблені методи, які спрощують цей процес. Коли кількість аргументів БФ не досить велика (до шести аргументів) найбільш ефективними є табличні методи мінімінізації. До них відносяться методи Вейча і Карно. По суті ці методи є однотипними і мають неістотні відмінності, зв’язані з формою зображення таблиці, яку в методі Карно називається картою, а в методі Вейча діаграмою.
Розглянемо докладніше метод діаграм Вейча. В цьому методі для мінімізації логічних функцій використовують діаграму Вейча, яка по суті є таблицею справжності, пристосованою для мінімінізації логічних функцій за критерієм простоти алгебраїчного виразу. Отже, діаграма Вейча, як і карта Карно, це прямокутна таблиця, кількість кліток якої для БФ n аргументів дорівнює кількості наборів функції, тобто 2n. Кожній з кліток діаграми Вейча відповідає свій набір значень аргументів БФ. Самі аргументи булевої функції розташовують на зовнішніх сторонах діаграми. Загальний вигляд діаграми Вейча для БФ двох, трьох і чотирьох аргументів показаний на рис. 3.2
На рис. 3.2 в кожній клітці діаграми вказані значення тих наборів аргументів x1x2x3x4, які їй відповідають. Значення кожного з аргументів БФ в межах відрізка прямої лінії, біля якої цей аргумент показано на зовнішній стороні діаграми Вейча, дорівнює 1, за межами відрізка – 0.
|
| Рис. 3.2. Діаграми Вейча для булевих функцій двох (а), трьох (б) і чотирьох (в) аргументів |
При заповненні діаграми Вейча в її клітках записують значення логічної функції, яке вона приймає на наборі аргументів, що відповідає даній клітці. Значення функції, яке дорівнює нулю можна не указувати. Таким чином, клітки діаграми Вейча, в яких записано значення 1, відповідають конституентам одиниці (мінтермам), а клітки із значенням 0 - конституентам нуля (макстермам)канонічної форми завдання булевої функції. При мінімізації булевих функцій за допомогою діаграм Вейча використовують табличний спосіб їх завдання. У випадку, коли логічна функція задана аналітичним виразом, цей вираз шляхом перетворень, описаних вище, приводять до ДДНФ і згідно їй заповнюють діаграму. Приклад заповненої діаграми для булевої функції Y(x1,x2,x3), яка задана табл. 3.1, показано на рис. 3.3а.
При заповненні діаграми в таблиці справжності виділяють набори, на яких БФ має одиничні значення. Клітку діаграми Вейча, яка відповідає заданому набору, знаходять з урахуванням того, що в клітках, розташованих в стовпцях або рядках в межах відрізків лінії, поряд з якими вказаний відповідний аргумент БФ, він приймає значення 1, а в клітках за межами цих відрізків - інверсне значення 0. В клітку діаграми, знайдену як зазначено вище, записують одиницю. Після того, як діаграма заповнена (рис. 3.3а), виконують мінімізацію булевої функції. Для цього у заповненій діаграмі Вейча виділяють сусідні набори, тобто такі, які відрізняються однією компонентою. Конституенти одиниці, які відповідають таким наборам, склеюються. Наприклад для функції Y(x1,x2,x3), заданої табл. 3.1, конституенти, що відповідають парі одиниць в лівій частині діаграми на рис. 3.3а склеюються і породжують елементарну кон’юнкцію з двох букв: 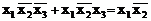 . Про пару одиниць в правій частині діаграми (рис. 3.3а) можна сказати теж саме:
. Про пару одиниць в правій частині діаграми (рис. 3.3а) можна сказати теж саме: 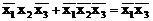 .
.

|
| Рис. 3.3. Діаграма Вейча для функції Y(x1,x2,x3), заданої табл. 3.1: а – після заповнення, б – після склеювання одиниць |
Зазначимо, що елементарні кон’юнкції, які виходять при склеюванні, легко визначити з діаграми Вейча – це добуток тих аргументів БФ, які мають однакові значення в клітках, що склеюються. Одиниці, які склеюються, обводять, як показано на рис. 3.3б. Зазначимо також, що стовпці і строки, розташовані по краях діаграми, також вважаються сусідніми, тому, як показано на рис. 3.3б, одиниці розташовані на початку і в кінці нижнього рядка діаграми Вейча (обведені пунктирною лінією) також можуть бути склеєні, що дає ще одну елементарну кон’юнкцію 
 . Отже, за результатами мінімізації булевої функції Y(x1,x2,x3), заданої табл. 3.1, отримані дві тупикові диз’юнктивні нормальні форми: Y1 = x1
. Отже, за результатами мінімізації булевої функції Y(x1,x2,x3), заданої табл. 3.1, отримані дві тупикові диз’юнктивні нормальні форми: Y1 = x1  +
+ 
 і Y2 = x1
і Y2 = x1  +
+ 
 +
+ 
 . З цих ТДНФ мінімальною є перша Y1, яка містить найменшу кількість букв. Вона і є МДНФ, яку треба вибрати як результат мінімізації логічної функції.
. З цих ТДНФ мінімальною є перша Y1, яка містить найменшу кількість букв. Вона і є МДНФ, яку треба вибрати як результат мінімізації логічної функції.
Загальне правило склеювання на діаграмах Вейча можна сформулювати так: склеюванню підлягають прямокутні конфігурації, заповнені одиницями, кількість кліток в яких є цілим ступенем числа 2, тобто 2, 4, 8 і так далі. Одержана за рахунок склеювання елементарна кон’юнкція визначається як добуток змінних, які зберігають своє значення на всіх наборах, що склеюються. Кількість m аргументів БФ, що залишаються у елементарній кон’юнкції після склеювання, визначається співвідношенням:
m = n – log2M,
де n – кількість аргументів функції; M – число наборів, що склеюються.
Якість мінімінізації оцінюють коефіцієнтом покриття
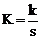 ,
,
де k – загальна кількість прямокутних конфігурації в межах яких виконують склеювання, s – сумарна кількості одиничних кліток для всіх прямокутних конфігурацій що склеюються.
Для діаграм Вейча чотирьох аргументів і менше знаходження прямокутних конфігурації сусідніх кліток, які містять одиниці, що склеюються, є досить простою процедурою. Для діаграм п’яти і більшої кількості аргументів процедура ускладнюється. Діаграму п’яти аргументів треба представляти у вигляді двох діаграм чотирьох аргументів, діаграму шести аргументів – у вигляді чотирьох діаграм чотирьох аргументів і так далі. Це ускладнює знаходження мінімальних покриттів, тому діаграми Вейча (карти Карно) використовують тільки для мінімізації булевих функцій, які залежать від невеликої кількості аргументів, звичайно, не більше чотирьох.
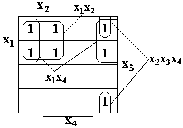
Розглянемо ще декілька прикладів мінімізації БФ за допомогою діаграм Вейча. Необхідно знайти МДНФ для функцій Y(x1,x2,x3,x4) і Z(x1,x2,x3,x4) заданих таблицями справжності, наведеними у табл. 3.5.
Діаграма Вейча для функції Y(x1,x2,x3,x4) після заповнення її одиницями і один з можливих варіантів склеювання одиниць показані на рис. 3.4. Результатом такого склеювання є тупикова ДНФ Y1 = x1x2+x1 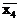 +
+ 

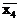 . Зазначимо, що можливі і інші варіанти склеювання одиниць. Наприклад, можна склеїти чотири одиниці на початку і дві одиниці в кінці перших двох рядків діаграми, а також останні одиниці у верхньому та нижньому її рядках. Це дасть ТНДФ Y2 = x1x2+x1
. Зазначимо, що можливі і інші варіанти склеювання одиниць. Наприклад, можна склеїти чотири одиниці на початку і дві одиниці в кінці перших двох рядків діаграми, а також останні одиниці у верхньому та нижньому її рядках. Це дасть ТНДФ Y2 = x1x2+x1 
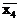 +
+ 

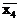 . Для першої ТНДФ коефіцієнт покриття K1 = 3/10 = 0,3, для другої – K2 = 3/8 = 0,38. Таким чином, у першому випадку покриття при склеюванні краще, ніж у другому. Тому тупикова форма Y1 містить меншу кількість букв і її треба обрати як результат мінімізації. Взагалі слід зазначити, що після заповнення діаграми Вейча склеювання треба виконувати таким чином, щоб покриття одиниць було найбільшим.
. Для першої ТНДФ коефіцієнт покриття K1 = 3/10 = 0,3, для другої – K2 = 3/8 = 0,38. Таким чином, у першому випадку покриття при склеюванні краще, ніж у другому. Тому тупикова форма Y1 містить меншу кількість букв і її треба обрати як результат мінімізації. Взагалі слід зазначити, що після заповнення діаграми Вейча склеювання треба виконувати таким чином, щоб покриття одиниць було найбільшим.
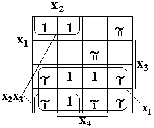
Особливістю функції Z(x1,x2,x3,x4) є те, що вона частково визначена. При заповненні діаграми Вейча для частково визначених БФ в клітках, що відповідають одиничним наборам, записують 1, а клітки, що відповідають наборам, на яких функція невизначена, позначають яким-небудь символ, наприклад, „~” або „*”. Заповнена діаграма Вейча для функції Z(x1,x2,x3,x4) показана на рис. 3.5. При обробці заповненої діаграми частково визначеної булевої функції клітки з невизначеними значеннями БФ доповнюють 1 або 0 таким чином, щоб покриття одиниць було найбільшим. Для діаграми Вейча на рис. 3.5 значення логічної функції, якими доповнені невизначені набори, показані нижче символу невизначеності „~”. Отже, результатом склеювання є мінімальна ДНФ  +x2
+x2  з коефіцієнтом покриття K = 2/12 = 0,17 і тому мінімізований аналітичний вираз для функції Z має вигляд Z(x1,x2,x3,x4) =
з коефіцієнтом покриття K = 2/12 = 0,17 і тому мінімізований аналітичний вираз для функції Z має вигляд Z(x1,x2,x3,x4) =  +x2
+x2  .
.
Таблиця 3.5
| 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 3.4. Діаграма Вейча і склеювання одиниць для логічної функції Y(x1,x2,x3,x4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 3.5. Діаграма Вейча і склеювання одиниць для логічної функції Z(x1,x2,x3,x4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Контрольні запитання
1. Дайте визначення логічної змінної, набору логічних змінних і логічної функції. Що є областю визначення логічної функції від n аргументів ?
2. Скільки існує логічних (булевих) функцій від n аргументів?
3. Що таке логічне заперечення, логічне додавання (диз’юнкція) та логічне множення (кон’юнкція) ? Напишіть таблиці справжності для булевих функцій НЕ, АБО, І.
4. Який порядок виконання логічних операцій при обчисленні логічних виразів ?
5. Запишіть у вигляді логічних виразів основні аксіоми і закони алгебри логіки та за допомогою них спростіть логічні вирази: а) x1x2 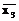 +x1x2x3+x1
+x1x2x3+x1 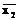
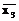 + x1
+ x1 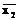 x3; б)
x3; б) 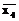 +x1x2
+x1x2 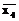 +
+ 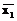 x2
x2 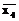 +
+ 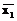
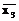 +
+ 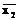
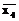 +
+ 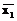
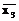 x2+
x2+ 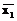
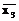
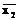 .
.
6. Які способи завдання булевих функцій найбільш часто використовують у алгебрі логіки ? Поясніть суть цих способів.
7. Що таке диз’юнктивна (ДНФ) та кон’юнктивна (КНФ) нормальні форми завдання булевих функцій ?
8. Функцію Y = x1 + x2 + 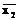
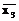 представте у ДДНФ, а функцію Z = x1(x1+x3)(
представте у ДДНФ, а функцію Z = x1(x1+x3)( 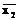 +
+ 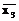 ) у ДКНФ.
) у ДКНФ.
9. Що таке конституента одиниці і конституента нуля ? Як за допомогою конституент нуля і одиниці записують ДКНФ і ДДНФ булевої функції безпосередньо з її таблиці справжності ?
10. Напишіть логічні вирази та таблиці справжності для булевих функцій І-НЕ, АБО-НЕ, складання за модулем 2, рівнозначності.
11. Що таке функціонально повні системи булевих функцій ? Приведіть приклади таких систем.
12. Методом Вейча мінімізуйте частково визначену булеву функцію Z(x1,x2,x3) задану табл. З.1, а також функцію Y(x1,x2,x3,x4) задану аналітичним виразом: Y(x1,x2,x3,x4) =
= x1 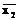
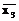
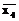 +
+ 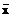 1x2
1x2 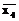 +
+ 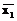
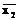
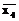 +
+ 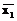
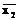 x3x4+
x3x4+
+ 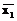
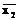
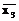 x4.
x4.
Розділ 4.ЛОГІЧНІ ЕЛЕМЕНТИ ЦИФРОВИХ ПРИСТРОЇВ
Дата добавления: 2018-04-05; просмотров: 931; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
