Вычисление определителей 2-го и 3-го порядков. Минор. Алгебраическое дополнение
Определитель 2-го порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях:.  Определитель 3-его порядка выражается в виде суммы, каждый член которой есть произведение трех элементов, взятых по одному и только по одному из каждой строки и каждого столбца. При вычислении определителей третьего порядка обычно пользуются правилом треугольников: первые три слагаемых в правой части равенства вычисляются так, как это показано на рис.
Определитель 3-его порядка выражается в виде суммы, каждый член которой есть произведение трех элементов, взятых по одному и только по одному из каждой строки и каждого столбца. При вычислении определителей третьего порядка обычно пользуются правилом треугольников: первые три слагаемых в правой части равенства вычисляются так, как это показано на рис.
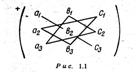
 они представляют собой произведения элементов, стоящих на главной диагонали и вершинах двух треугольников, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемых правой части равенства вычисляются аналогично рис. только за основу взята побочная диагональ. Причем эти слагаемые берутся с обратным знаком.
они представляют собой произведения элементов, стоящих на главной диагонали и вершинах двух треугольников, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемых правой части равенства вычисляются аналогично рис. только за основу взята побочная диагональ. Причем эти слагаемые берутся с обратным знаком.
Так же прибегая к разложению по строке или столбцу можно перейти к более простому определителю 2-го порядка:

Опр. Если из определителя  n-го порядка вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то получится определитель (n-1)-го порядка, называемый минором определителя
n-го порядка вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то получится определитель (n-1)-го порядка, называемый минором определителя  , соответствующий этому элементу. Опр. Алгебраическим дополнением некоторого элемента называется соответствующий ему минор, взятый со знаком + или – , смотря по тому, будет ли сумма номеров строки и столбца, которым принадлежит данный элемент, чётным или нечётным.
, соответствующий этому элементу. Опр. Алгебраическим дополнением некоторого элемента называется соответствующий ему минор, взятый со знаком + или – , смотря по тому, будет ли сумма номеров строки и столбца, которым принадлежит данный элемент, чётным или нечётным.
|
|
|
Вычисление определителей n-ого порядка. Треугольные диагональные матрицы.
Определитель n-ого порядка можно вычислить по формуле:

т. е. Вычисление определителей n-ого порядка можно свести к вычислению n - определителей (n-1)-го порядка.  - разложение по i-той строке,
- разложение по i-той строке,  - разложение по j-тому столбцу.
- разложение по j-тому столбцу.
Определитель n – ого порядка можно считать двумя способами:
1. Разложением по удобной строке или столбцу. 2. Используя знакомые операции над строками или столбцами определителя. Часто используется комбинация этих двух способов.  ,
, 
det(A-1*A)=detA-1*detA =1. Одним из видов матриц являются диагональные матрицы, они имеют вид:
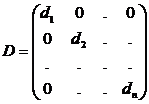 , подвид диаг. матрицы-треугольная:
, подвид диаг. матрицы-треугольная: 
Решение матричных уравнений. Примеры. Их связь с формулами Крамара.
1.  -
-  (detA
(detA  0)
0)
2. 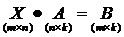 -
- 
(detA  0)
0)
3.  -
- 
(detA 
Если detA=0  , либо пустое множество. При желании матричное уравнение можно привести к системе линейных уравнений относительно n – кол-ва неизвестных.
, либо пустое множество. При желании матричное уравнение можно привести к системе линейных уравнений относительно n – кол-ва неизвестных.
Системы линейных уравнений. Матричная и векторная запись. Основные понятия.
Опр. Система вида:  называется СЛУ матричный вид записи:
называется СЛУ матричный вид записи:  , где A – матрица системы, Х-столбец неизвестных, В - столбец свободных членов.
, где A – матрица системы, Х-столбец неизвестных, В - столбец свободных членов.
векторный вид записи: 
По внешнему виду СЛУ делятся на однородные и неоднородные. По типу решения системы делятся: 1. совместные (имеют хотя бы одно решение), 2. несовместные (не имеют решений).
|
|
|
Опр. Упорядоченный набор чисел С1…Сn называется решением системы, если при подстановке x1=C1, xn=Cn, и все уравнения системы превращаются в тождества. Система СЛОУ – всегда совместная. Совместные системы можно разделить на: 1. определённые – имеющие одно решение 2.неопределённые – имеющие более одного решения. Опр. Две системы называются эквивалентными, если они имеют одинаковое множество решений или они обе несовместные. Главный способ решения СЛОУ - привидение исходной системы к более простой эквивалентной с помощью следующих элементарных преобразований. Принцип решения: 1. меняем местами любые два ур-я. 2. любое Ур-е можно умножить или сократить на число 
 . 3. решение системы не изменится, если любое Ур-е заменить на его сумму с другим уравнением, умноженным на любое число. 4. данные экспериментальные преобразования строк матрицы a. меняются местами любые две строки. b.
. 3. решение системы не изменится, если любое Ур-е заменить на его сумму с другим уравнением, умноженным на любое число. 4. данные экспериментальные преобразования строк матрицы a. меняются местами любые две строки. b. 
с.  . Можно привести к ступенчатому виду. По полученной ступенчатой матрице получаем систему уравнений соответствующего вида, которая имеет более простой вид с точки зрения решения и является эквивалентной исходной.
. Можно привести к ступенчатому виду. По полученной ступенчатой матрице получаем систему уравнений соответствующего вида, которая имеет более простой вид с точки зрения решения и является эквивалентной исходной.
|
|
|
Дата добавления: 2018-04-04; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
