Понятие конечных разностей. Общий вид интерполяционной формулы Ньютона

Для получения интерполяционной формулы Ньютона более общего вида введём следующие обозначения:

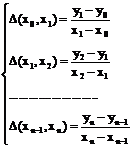разностные отношения 1-го порядка;

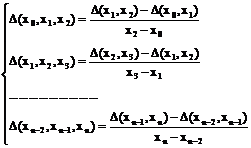разностные отношения 2-го порядка и так далее:

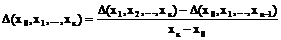разностные отношения к-го порядка.

Вычисление разностных отношений, как и конечных разностей, сводится в таблицу.

n	x_i	y_i	D(x_i,x_i+1)	D(x_i,x_i+1,x_i+2)	D(x_i,x_i+1, x_i+2 x_i+3)	D(x_i,…, x_i+4)
1	x₀	y₀
2	x₁	y₁	D(x₀,x₁)
3	x₂	y₂	D(x₁,x₂)	D(x₀,x_1,x₂)
4	x₃	y₃	D(x₂,x₃)	D(x₁,x₂,x₃)	D(x₀,x1,x₂,x₃)
5	x₄	y₄	D(x₃,x₄)	D(x₂,x_3,x₄)	D(x₁,x₂,x_3,x₄)	D(x₀,x₁,x₂,x_3,x₄)

На основании этой таблицы можно составить интерполяционный многочлен Ньютона который представляется в виде:

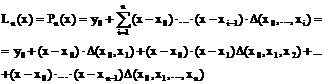
Фактически для составления интерполяционного многочлена разностные отношения этого многочлена необходимо списать из верхней строки таблицы.

П р и м е р. Функция y=f(x) задана таблично:

x	0,4	0,55	0,65	0,8	0,9	1,05
y	0,41075	0,57815	0,69675	0,88811	1,02652	1,25380

Построить интерполяционный многочлен Ньютона и найти его значение в точке x₀=0,596.

Решение

x	y	D(x_i,x_i+1)	D(x_i,x_i+1,x_i+2)	D(x_i,x_i+1, x_i+2 x_i+3)	D(x_i,…, x_i+4)
0,4	0,4108
0,55	0,5782	1,116
0,65	0,6968	1,186	0,28
0,8	0,8881	1,2757	0,3589	0,1973
0,9	1,0265	1,3841	0,4335	0,213	0,034
1,05	1,2538	1,5152	0,5244	0,2273	0,034

Из таблицы видно, что разностные отношения четвёртого порядка постоянны. Поэтому будем интерполировать функцию многочленом Ньютона четвёртого порядка.

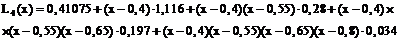Подставив в полученный многочлен заданную точку, получим L₄(0,596)=0,63192.

З а м е ч а н и е 1. Существует связь между разностными отношениями и конечными разностями при равноотстоящих узлах. Эта связь выражается формулой

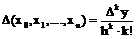З а м е ч а н и е 2. Если интерполируемая функция является многочленом n-ой степени, то разностные отношения n-го порядка будут постоянными величинами, а отношение (n+1)-го порядка равно 0.

Погрешность алгебраического интерполирования

Очевидно, что всякое интерполирование - это лишь приближенный подбор функции. Причём степень такого приближения может быть разная. Поэтому важной задачей является оценка погрешности интерполирования.

Исходя из основного интерполяционного тождества можно заметить, что значения интерполируемой f(x) функции и интерполирующего полинома j_n(x) совпадают только в узлах интерполяции (x_i; y_i), . Между узлами функция j_n(x) может вести себя произвольным образом, сколь угодно далеко отклоняясь от зависимости f(x). Определить погрешность приближения можно, используя выражение для абсолютной ошибки e=max|f(x) – j_n(x)|. Однако, такая оценка возможна только в том случае, когда исходная функция задана аналитически.

Аналитически погрешность алгебраической интерполяции можно вычислить по следующей формуле:

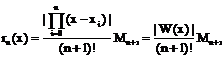. (20)

где 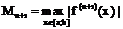– максимальное значение (n+1)-й производной функции f(x) по абсолютной величине на отрезке [a; b].

Из формулы видно, что вклад в погрешность вносят три компоненты: произведение разностей по абсолютной величине 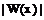, максимальное значение (n+1)-й производной M_n₊₁ функции f(x) по абсолютной величине на отрезке [a; b] и величина факториала (n+1)!. Причём факториал и произведение разностей с увеличением n уменьшают ошибку, однако порядок производной при этом растет. Для многих функций величина M_n₊₁ увеличивается быстрее, чем величина факториала в знаменателе. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции. Для большинства функций с повышением степени интерполирующего полинома погрешность возрастает. Поэтому на практике использование интерполянтов выше пятой степени считается нецелесообразным.

При равномерном разбиении исходного отрезка остаточный член интерполяции примет вид

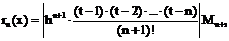(21)

Однако применение формул (20) и (21) затрудняется в сложности оценки величины M_n₊₁. При интерполировании по формуле Ньютона эта задача решается проще – остаточный член вычисляется следующим образом

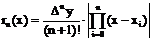, (22)

где 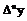– можно считать как среднее арифметическое конечных разностей n порядка.

Точность приближения зависит не только от числа узлов интерполирования (т.е. порядка интерполирующего полинома), но и от их расположения на выбранном отрезке [a; b]. В простейшем случае выбирается равномерное расположение точек (x_i, y_i), 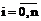на интервале [a; b] с шагом h=(b–a)/(n–1). Однако, как показывает практика, равномерное расположение не является оптимальным с точки зрения лучшего приближения j(x) к зависимости f(x). Доказано, что оптимальным для интерполяции является расположение узлов на интервале [a; b] по формуле Чебышева

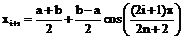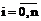(23)

Задания, рекомендуемые

Для аудиторных занятий

1. Для функции, заданной таблицей, воспользовавшись основным интерполяционным тождеством, составить систему линейных уравнений и найти неизвестные параметры интерполяционного полинома.

х	1	3	4
у	-8	2	6

По полученному полиному подсчитать значение в точке x=5,678

2. Для таблично заданной функции получить алгебраический, тригонометрический и экспоненциальный интерполянт.

х	1,23	2,396	4,5	5,2
у	0,882384	0,417701	0,355974	0,352112

Оценить погрешность каждого из интерполирований, совместив на одной координатной плоскости графики полученных интерполянтов и график исходной функции. Выбрать наилучшее приближение.

3. Для функции у = cos(2,5x) построить интерполяционный полином Лагранжа, выбрав узлы: х₀ = 0, х₁ = 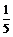, х₂ = 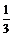. Найти погрешности результатов, путём сравнения их со значениями интерполируемой функции f(x).

4. Дана таблица значений функции у = f(x)

х	1	2	4	5
у	6	8	10	9

Вычислить f(3,5), используя интерполяционную формулу Лагранжа. Показать графически выполнение основного интерполяционного тождества.

5. Дана таблица значений функции у = f(x)

х	1,0	2,0	3,0	4,0
у	12	5,5	3,2	7

Построить интерполяционные полиномы, используя первую и вторую интерполяционные формулы Ньютона.

6. Пользуясь интерполяционными формулами Ньютона вычислить значения функции в точках х = 0,1 и х = 0,9 для функции у = f(x), заданной таблично

х	0	0,2	0,4	0,6	0,8	1,0
у	1,2	2,4	3,6	4,8	5,9	7,1

7. Имея таблицу значений функции у=sin(x)

х	15 º	20 º	25 º	30 º	35 º	40 º	45 º	50 º	55 º
у	0,2588	0,342	0,4226	0,5	0,5736	0,6428	0,7071	0,7660	0,8192

и оценить погрешность вычислений на заданном отрезке.

8. Для функции у=sin(x + e^sin^x) на отрезке [0; 3] получить 5 точек разбиения при равномерном распределении и распределении по формуле Чебышева. Для полученных табличных функций найти соответствующие интерполянты и погрешности формул. Сделать вывод.

Вопросы для самопроверки

1. Какое из понятий более общее: интерполяция, аппроксимация, экстраполяция?

2. В чем состоит различие между интерполяцией и экстраполяцией?

3. Для чего нужна интерполяция функций?

4. Охарактеризуйте виды интерполяции.

5. Какое условие должно быть выполнено при интерполяции?

6. Как связана степень интерполяционного многочлена с количеством узлов интерполяции?

7. Как будет выглядеть основное интерполяционное тождество для алгебраической интерполяции при задании 4 узлов и узловых значений интерполируемой функции?

8. Как будет выглядеть основное интерполяционное тождество для тригонометрической интерполяции при задании 4 узлов и узловых значений интерполируемой функции?

9. Как будет выглядеть основное интерполяционное тождество для экспоненциальной интерполяции при задании 5 узлов и узловых значений интерполируемой функции?

10. Как строятся интерполяционные многочлены Лагранжа и Ньютона? В чем особенности этих двух способов интерполяции?

11. Какие виды глобальной интерполяции вам известны?

12. Какие интерполяционные формулы применяются, если узлы интерполяции равноотстоящие?

13. Что такое конечные разности?

14. Как выглядят разностные отношения?

15. Какую интерполяционную формулу Ньютона необходимо применять в начале таблично заданной функции, и какую - в конце? Почему?

16. Сколько интерполяционных полиномов можно построить при заданном наборе узлов интерполяции?

17. Чем обуславливается выбор способов реализации формулы алгебраической интерполяции?

18. Какие способы повышения точность интерполяции Вы знаете?

19. Какие способы оценки погрешности интерполяций Вы знаете?

Индивидуальные Задания

Дата добавления: 2018-04-04; просмотров: 754; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!