Алгебраическое интерполирование

Введение

Одним из наиболее интересных разделов прикладной математики является теория приближения (аппроксимации) функций. Под приближением функции понимают замену по определенному правилу одной функции – аппроксимируемой f(x), другой – t(x), близкой к исходной в том или ином смысле. Функция t(x) при этом называется аппроксимирующей функцией. Практическая необходимость в такой замене возникает в самых различных ситуациях, когда данную функцию необходимо заменить более простой и удобной для вычислений, восстановить функциональную зависимость по экспериментальным данным и т.п.

В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной илидискретной.Если же аппроксимация проводится на непрерывном множестве точек (исходная функция задана явно), аппроксимация называется непрерывнойили интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

В ситуации, когда аппроксимирующая функция ищется так, чтобы её значения совпадали со значениями аппроксимируемой функцией в заданном наборе точек, процесс отыскания функции будем называть интерполяцией. Если же по набору точек следует восстановить приближённые значения функции вне заданного интервала, то данный процесс будем называть экстраполяцией функций. При этом, если интерполирующая функция едина для всей области интерполяции, говорят, что интерполяция глобальная, иначе, когда между различными узлами функциональные зависимости различны, говорят о кусочной или локальной интерполяции.

Основоположником теории аппроксимации функций является великий русский математик Пафнутий Львович Чебышев (1821-1894).

В представленных методических указаниях рассмотрен один из основных способов аппроксимации функций – глобальное интерполирование.

Глобальное интерполирование функций

Основные понятия и постановка

Задачи интерполяции функции

Интерполирование первоначально рассматривалось как нахождение промежуточных значений функции по известным значениям заданных узлов (термин интерполирование означает чтение между строк).

Интерполирование – задача обратная табулированию. При табулировании по аналитически заданной функции находят значения в узлах, а при интерполировании – по узловым значениям находят промежуточные значения функции.

x	x₁	x₂	…	x_n
f(x)	f(x₁)	f(x₂)	…	f(x_n)

С геометрической точки зрения это означает, что между интерполяционными узлами можно провести линию, соответствующую выбранной функции.

Основной задачей интерполирования является подбор функции приближающей её значения с значениями в заданных узлах. Из рис. 1 следует, что выбор такой функции неоднозначен. А такие задачи решать сложно.

Однако если на искомую функцию наложить дополнительные ограничения, то в этом случае задача может быть решена.

Задача интерполяции состоит в следующем: заданы точки (x_i, y_i), , требуется найти функцию t(x), которая проходит через эти точки (рис. 1), т.е.

t(x_i)=y_i ,

(1)

Точки (x_i, y_i) называют узлами интерполяции, а функцию t(x) – интерполирующей функцией или интерполянтом.

Как правило, в качестве интерполирующей функции используют обобщенный многочлен t(х) на системе линейно-независимых функций.

Линейно-независимыми называются функции линейная комбинация которых 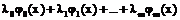равна 0, в случае когда все l_k=0 ( )

Если j₁(х), j₂(х), …, j_m(х) система линейно-независимых функций, то обобщенный многочлен t(х) на системе линейно-независимых функций примет вид

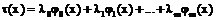Совокупность функций j₁(х), j₂(х), …, j_m(х) называется системой Чебышева на отрезке [a; b] если любой обобщённый многочлен по этой системе, у которого хотя бы один из коэффициентов отличен от нуля, имеет на данном отрезке не более n корней.

Справедливо следующее утверждение: для любого n+1 узла x₀, x₁,…, x_n на [a; b] существует единственный обобщённый интерполяционный многочлен тогда и только тогда, когда система функций j_k(х) k= являлась системой Чебышева на данном промежутке.

Пусть интерполирующая функция имеет следующий вид:

(2)

где j₀(x), j₁(x),…, j_m(x) – базисные функции.

Используя условие (1) и выражение (2), получаем систему уравнений

(3)

Система (3) будет иметь единственное решение в случае когда:

1) число точек (x_i, y_i), равно числу коэффициентов c_k, ;

2) система уравнений (3) является невырожденной, т.е. определитель системы D¹0.

Таким образом, если выполняются вышеуказанные условия, то через точки (x_i, y_i) проходит единственная функция .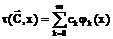

Вид обобщённого многочлена t(x) определяет способ интерполяции. Существуют 3 основные группы функций, широко применяемых в численном анализе. Первая – включает в себя линейные комбинации функций 1, х, х², …, хⁿ, что совпадает с классом всех многочленов степени n. Вторую – образуют функции 1, sin(x), cos(x),…, sin(nx), cos(nx). Этот класс имеет отношение к рядам Фурье и интегралу Фурье. Третья – образуется функциями . Эти функции встречаются в реальных ситуациях при решении задач накопления и распада. Если в качестве системы линейно-независимых функций в обобщённый многочлен входят степенные функции {1, х², …., хⁿ} –интерполяцию называют алгебраической; {sin(x), cos(x),…, sin(nx), cos(nx)} – тригонометрической; { 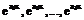} – экспоненциальной.

Алгебраическое интерполирование

На практике в качестве интерполирующей функции t(x) часто используются алгебраические полиномы, так как их легко вычислять, дифференцировать и интегрировать. При этом интерполяция носит название алгебраической.

Для однозначности решения этой задачи потребуем, чтобы искомой функцией был многочлен степени на единицу меньшей, чем число заданных узлов и в узловых точках значения совпадали. В этом случае базисными функциями будут:

j₀(x)=x⁰=1, j₁(x)=x¹=x, j₂(x)=x²,…, j_n-1(x)=xⁿ^-1, j_n(x)=xⁿ ,

а интерполяционный многочлен будет иметь вид:

t(x)= L_n (x)=с₀+с₁×x+с₂×x²+…+с_n×xⁿ. (4)

Существуют различные подходы к определению неизвестных параметров интерполяционного многочлена. Основные из них:

1) с помощью составления системы линейных уравнений;

2) по формуле Лагранжа;

3) по формулам Ньютона.

Дата добавления: 2018-04-04; просмотров: 919; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!